多航天器部署问题中的自主导航方法研究

钱霙婧，荆武兴，高长生

(哈尔滨工业大学 航天工程系，哈尔滨 150001，qianyingjing@yahoo.com.cn)

多航天器部署问题中的自主导航方法研究

钱霙婧，荆武兴，高长生

(哈尔滨工业大学 航天工程系，哈尔滨 150001，qianyingjing@yahoo.com.cn)

以恒星和地球方位矢量夹角作为观测量，用迭代最小二乘法为滤波算法来确定历元时刻的状态，并以预报方式实现自主导航的方法研究多航天器部署问题中被动段导航问题.通过数学仿真，分析比较了采样周期、采样弧长、敏感器精度、恒星方位等因素对于定位精度的影响，总结了其变化规律，并给出了安装因素对于导航精度的影响.与测量因素相对比，结果表明前者对导航精度的影响更大.

多航天器部署;自主导航;最小二乘法

多航天器部署即由运载器一次性携带多颗航天器，在空间经过多次轨道机动实现多航天器发射任务.在多航天器部署任务期间需要使用适当的导航方法实现定轨，为轨道机动提供足够精度的导航信息.与美国国情不同，我国并不拥有GPS的所有权.若单纯依靠地面测轨的方法确定轨道并生成制导信息，不仅易受干扰、运营昂贵而且部署周期会因地面测控圈数的限制变长.多航天器部署导航任务分为主动段和被动段两类.其中，由于主动段时间较短，惯性导航系统漂移并不严重，因此只要被动段提供精确的初始条件，仅用惯导系统就能给出高精度的导航信息.

本文采用恒星方位矢量和地球方位矢量的夹角作为观测量(这两种敏感器本身也是姿态敏感器，将其信息用于自主导航不会增加航天器的载荷质量).考虑到运载器只需在机动点有精确的数据，较长弧段的被动飞行为采用最小二乘方法提供了批处理的机会，因此利用最小二乘法确定历元时刻的运载器状态，并以预报的方式实现运载器的自主导航，为主动段提供初始条件.文中通过数学仿真对这种自主导航方式进行验证，并分析了采样弧长、采样周期、敏感器精度、恒星方位、敏感器安装误差对历元时刻定位精度的影响.

1 多航天器部署导航方案

由于地面站最后注入的导航数据存在较大的误差，因而，在机动点机动后运载器进入的并不是精确目标轨道，而是误差目标轨道.

基于上述分析，对于多航天器部署任务提出导航方案为:运载器在机动点机动进入误差目标轨道后，在误差目标轨道上飞行一周，自主导航系统利用一周的飞行数据为更准确地进入精确目标轨道提供导航信息.运载器飞行轨迹如图1所示.从内向外依次为转移轨道、误差目标轨道和精确目标轨道.

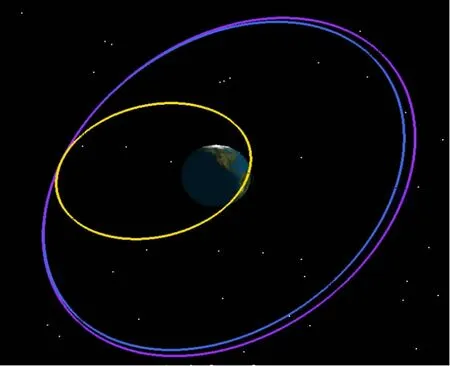
图1 飞行轨迹图

2 运载器轨道信息的自主确定

2.1 导航动力学方程

首先定义建立运载器轨道动力学方程中两个坐标系.

1)J2 000.0地心赤道坐标系.原点定义在地心，基准平面是赤道平面，X轴方向指向J2 000.0历元时刻的平春分点，Z轴指向平北极，Y轴构成右手直角坐标系.

2)运载器轨道坐标系.以运载器的质心为原点，z轴由运载器指向地心，x轴在运载器瞬时轨道面内指向运载器速度方向，并垂直于z轴，y轴沿瞬时轨道平面的负法线方向，与x轴、z轴形成右手直角坐标系.文中假设运载器的体坐标系与轨道坐标系重合.

在J2 000.0地心赤道坐标系中，运载器的轨道动力学模型为［1］

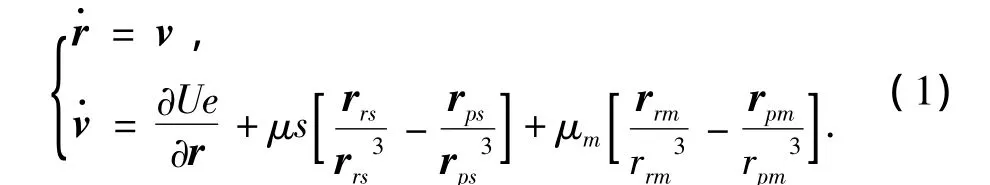
2.2 导航观测方程与滤波算法

星载敏感器的观测量均是运载器本体坐标系下的量，它们包括恒星一方位矢量ra1、恒星二方位矢量rb1、地球方位矢量r1，如图2所示.

图2 星载敏感器观测示意图

假设已知运载器轨道和世界时，则可以计算出运载器在地心J2 000惯性坐标系下的坐标r，基于恒星敏感器模型可以获得恒星方位的计算值ra，rb.因此可确定地球方位和两导航星方位之间的方位夹角计算值，则观测模型为［2－5］

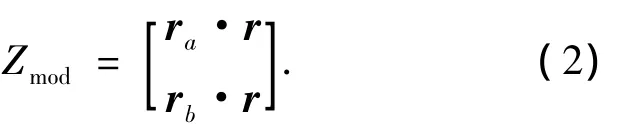
式中:Zmod为r0v0和t的函数.

由敏感器测量得到的两恒星和地球之间的方位夹角测量值为

则残差方程为

式中:G为r0v0的函数，r0v0的初始猜测误差对残差大小起决定作用，但真正的r0v0应当使残差范数最小.在 N 个采样时刻 t0，t1，…，tN－1上的残差记为G(r0，v0，t0)，G(r0，v0，t1)，…，G(r0，v0，tN－1).

数值仿真经验表明，迭代过程进行4～6次即可得到精确结果.因此，将迭代次数作为计算终止条件.

计算步骤为:

1)迭代赋初值;

3)计算第一次迭代值，返回1).

3 仿真结果与精度分析

运载器在转移轨道远地点附近经过变轨进入误差目标轨道.在误差目标轨道被动飞行阶段假设不再得到地面系统的支持，此时启动自主导航方案，并采用10组飞行实验取统计值的方法逐一分析不同的误差因素对于导航精度的影响.根据国内外经验，结合国内的实际情况，运载器在目标轨道上基本应当保持在32 000 km高度.因此，对导航系统进行仿真时，假设为:

仿真模型:地球引力、地球形状摄动函数取J 2，J 3，J4项，考虑大气阻力、太阳和月球引力.

滤波模型:地球引力、地球摄动函数取J2项;

仿真历元时刻:2010－06－01;

坐标系:J2 000.0;

测量频率:每10 s进行一次测量;

敏感器测量精度:地球敏感器的测量精度为0.05°(3σ)星敏感器的测量精度为1×10－4rad;

初始轨道参数:远地点高度32 000 km，近地点高度30 000 km，轨道倾角55°，近地点幅角30°，真近角 360°;

滤波初始误差:位置10 km，速度5 m/s.

3.1 仿真结果

根据上述仿真条件，利用模拟的星载敏感器测量数据和DE405星历表，在运载器运行约一周(941 min)的范围内进行采样，在PC机上进行仿真计算，J2 000.0地心赤道坐标系下的仿真结果如表1所示.

表1 导航结果及其精度

表1中无噪声的情况下，验证了本文所采用的导航算法的方法精度.由表1中数据可知，位置估计误差达到了1×10－10km，速度估计误差达到了1×10－14km/s，由此可见，导航算法的具有较高的方法精度.表1中引入星敏感器、地球敏感器测量误差后的情况下，位置误差在0.45 km以下，速度估计误差在4.5×10－5km/s以下.

利用表1中带有观测噪声情况下的单点定位估计结果作为历元时刻的运载器状态，并由此向前进行预报20 min，其导航精度结果如图3所示.虚线、点划线、直线分别为X、Y、Z轴方向的变化.

图3 利用迭代最小二乘法预报20 min的导航误差历程

由图3可见，利用迭代最小二乘法确定的历元时刻运载器状态向前预报20 min，位置矢量的最大误差为0.5 km，速度矢量的最大误差6×10－5km/s.

3.2 影响历元时刻定轨精度的因素分析

运载器自主导航的精度由采样周期、敏感器测量精度等因素决定.本文利用最小二乘法确定历元时刻的运载器状态，并以预报的方式实现运载器的自主导航，为主动段提供初始条件.

3.2.1 采样周期选取分析

由于采用迭代最小二乘法为滤波算法，因而，采样周期的选取对于导航算法计算量的大小具有显著影响.采样周期越短，样本数据量越大，运载器历元时刻的定位精度就越高，从这个方面考虑，采样周期越短越好.但过大的样本数据量会直接导致处理数据所耗费时间过长.

在其他因素相同的情况下，分别选取采样周期为 2， 5， 10， 15， 20， 30，60 s进行仿真.图 4(a)～图4(c)分别为各种采样周期条件下，历元时刻、采样终点时刻、预报终点时刻的导航位置精度随采样周期的变化曲线.图4(d)～图4(f)分别为不同周期下，历元时刻、采样终点时刻、预报终点时刻的导航速度精度随采样周期的变化曲线虚线、点划线、直线分别为X、Y、Z轴方向的变化.

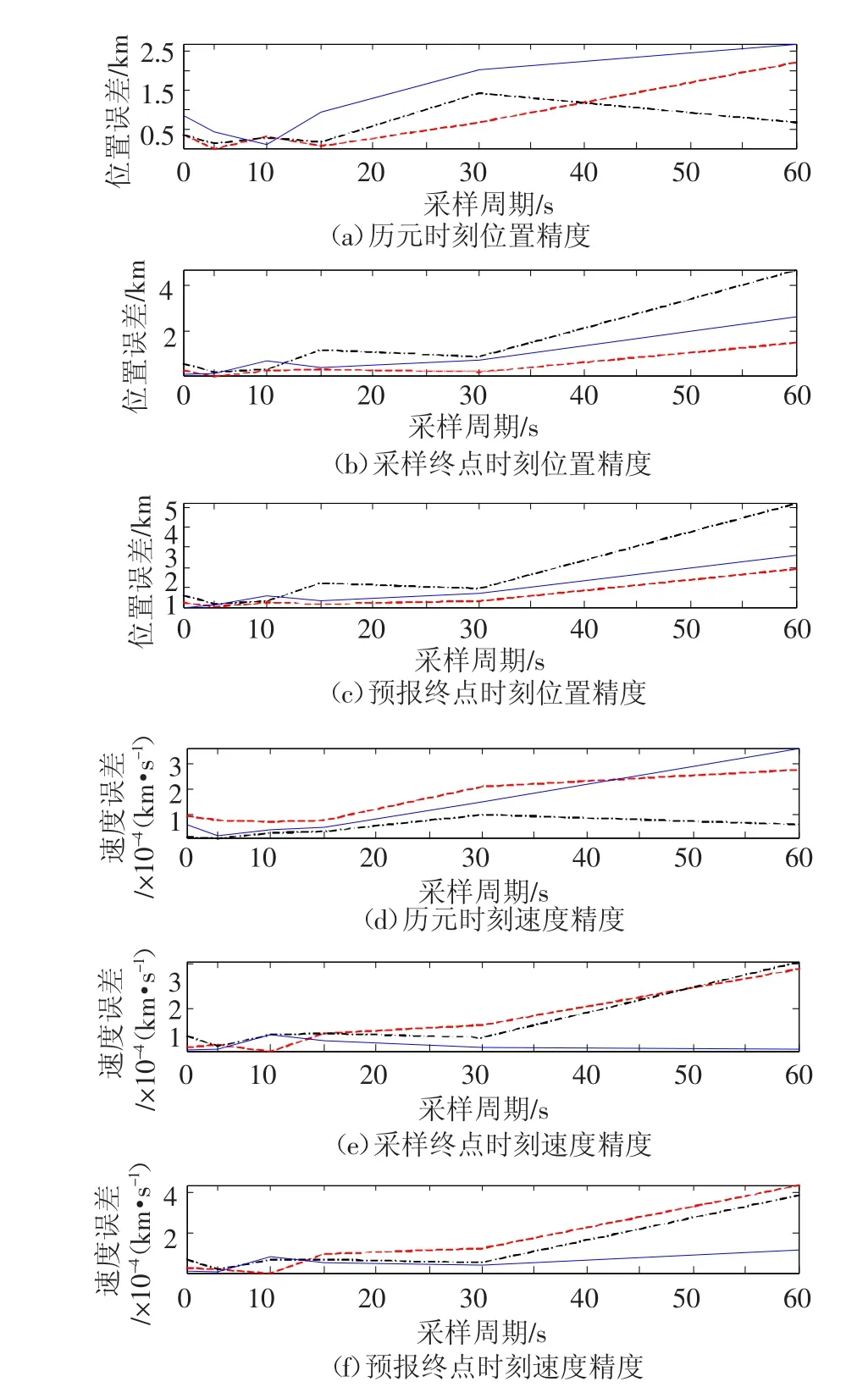
图4 不同采样周期时的导航精度

从图4中的数据可知，采样周期越短，样本数据越多，则导航精度越高.通过几组仿真实验可以发现，采样周期在20 s时或者＞20 s时，导航误差均较大，位置误差在1.5 km以上，速度误差在1.3×10－4km/s以上;采样周期减小至10 s时导航精度已经达到较高的水平，位置误差在0.8 km以下，速度误差在0.75×10－4km/s以下.但是，继续减小采样周期时导航精度的提高并不大，因而，在同时考虑精度与计算量的要求下，本文选择10 s为采样周期.但实际应用时，应当根据具体的星载计算机的计算和存储能力来确定采样周期.3.2.2 其他测量因素对导航精度的影响

1)采样弧长.在采样周期都是10 s，各种参数相同，仅有采样弧长不同的情况下，对于误差目标轨道上的自主导航进行仿真，J2 000.0地心赤道坐标系下的仿真结果如表2所示.

由表2中的数据可见，导航采样弧长越长，样本数据越多，则导航精度越高.当采样弧长减少到半圈时，位置估计误差已经上升到1 km以上，速度估计误差已经上升到1×10－4km/s的数量级.

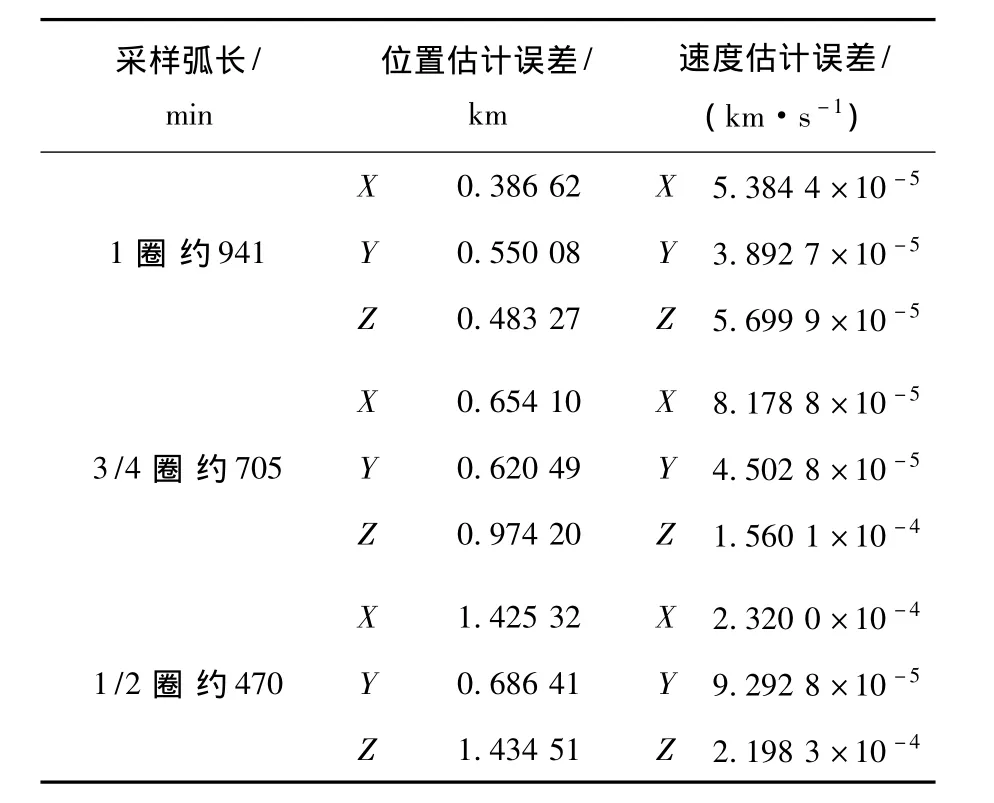
表2 采样弧长对于导航精度的影响

2)敏感器精度.在采样周期都是10 s，各种参数相同，仅有敏感器精度不同的情况下，对于误差目标轨道上的自主导航进行仿真，结果如表3所示.

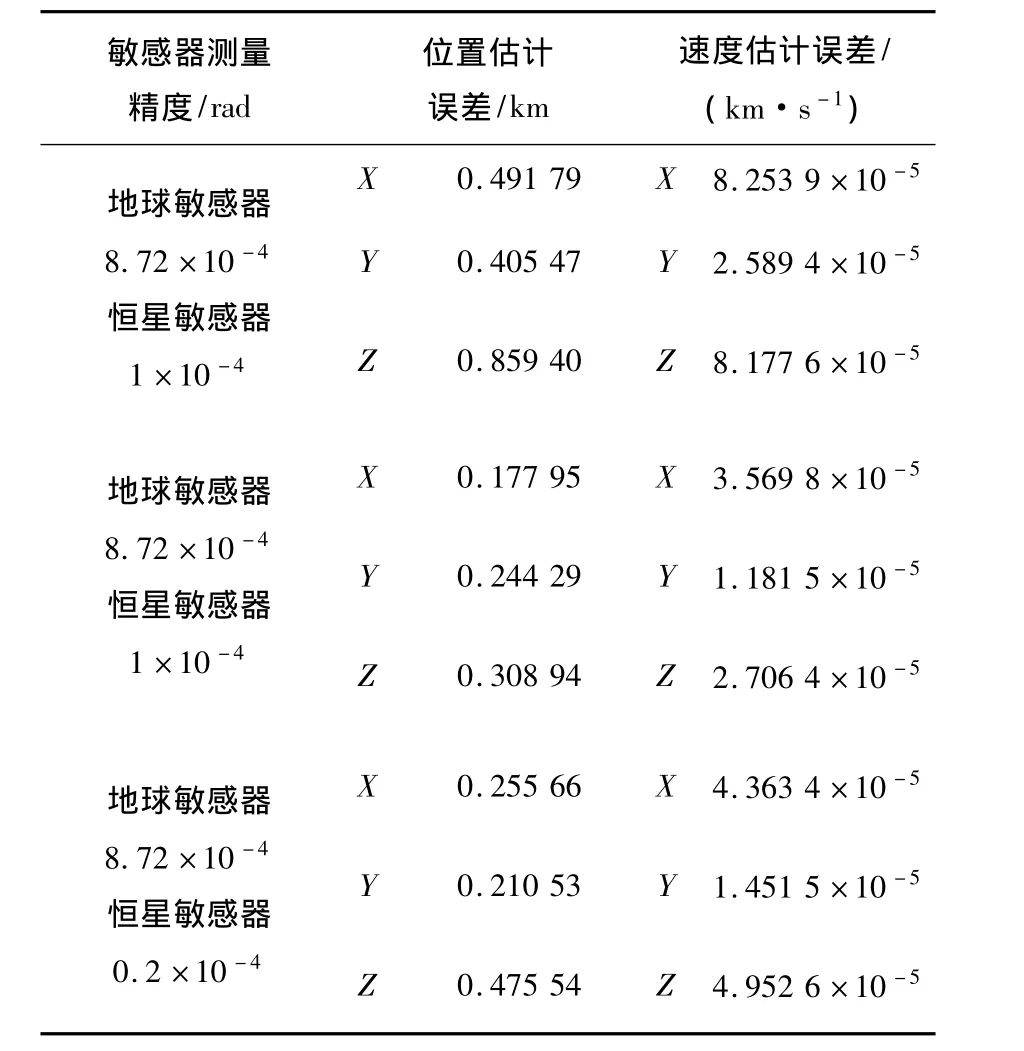
表3 敏感器精度对于导航精度的影响

比较表3中第1组和第2组的数据，可以发现当地球敏感器的精度提高1.5倍时，历元时刻的位置估计误差和速度估计误差分别是原来的0.35和0.42.比较表3中的第1组和第3组数据，可以发现当星敏感器精度提高1.5倍时，历元时刻的位置估计误差和速度估计误差分别是原来的0.53和0.61.由上述分析可见，与恒星敏感器精度相比，地球敏感器的精度对于导航精度的影响较大.

3)恒星方位选取的影响.由于文中依靠恒星的方位矢量进行导航，因而选择不同的恒星必然会对导航结果产生影响，文中采用3种选星方案，在各项条件相同的情况下进行仿真，结果如表4所示.

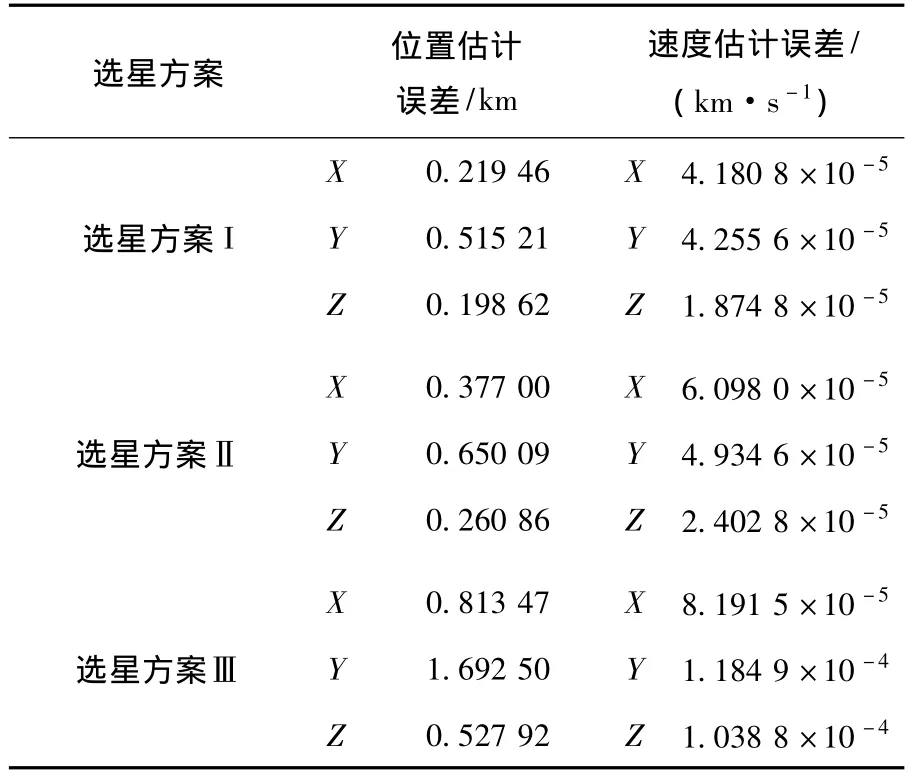
表4 恒星方位对于导航精度的影响

选星方案Ⅰ:一个恒星方位在轨道平面内，另一恒星位于轨道法线方向，且两恒星之间成90°的夹角;选星方案Ⅱ:两恒星方位与地球方位矢量之间，三者互称成90°的夹角;选星方案Ⅲ:一个恒星方位在轨道平面内，另一恒星于与轨道平面成60°角的方向.

由表4中仿真结果可知，在两恒星方向相互垂直的情况下，方案Ⅰ和方案Ⅱ都具有较高的导航精度且差别不大，都保持在位置估计误差0.6 km以下，速度估计误差6×10－5km/s以下，而且精度较高.当两恒星方位不垂直的时候，仿真精度有明显的下降.

3.2.3 安装因素对于导航精度的影响

除此之外，安装误差也是影响导航结果的重要因素.现以安装误差为0.008 3°和0.016 7°分别进行仿真，结果如表5所示.

表5 安装误差对于导航精度的影响

比较表5中第1组和第2组数据可知，当安装误差成倍增加后，导航误差也随之成倍增加.

另外，分别观察表3与表5可以发现，当地球敏感器误差0.05°，恒星敏感器误差1×10－4rad时所引起的位置估计误差和速度估计误差的数量级分别为0.1 km和10－5km/s.当安装误差为0.008 3°远远小于敏感器误差时，引起的位置估计误差和速度估计误差的数量级分别为1 km和10－4km/s.由上述分析可知，安装误差对于导航精度的影响更为明显，在实际工程中，在敏感器安装方面当引起重视.

4 结论

1)利用运载器在轨运行一周的观测数据进行20 min预报，最大位置误差为0.5 km，最大速度误差为6×10－5km/s.

2)在同时考虑导航精度要求与计算量要求的情况下，选取10 s为采样周期较好.

3)结果表明，采样弧长越长精度越高;地球敏感器相对星敏感器对于导航精度的影响更大;选星方案保持两恒星夹角90°时，导航效果较好;

4)安装误差相对测量误差对于导航精度的影响更大.在敏感器安装方面应当引起重视.

［1］章仁为.卫星轨道姿态动力学［M］.北京:北京航空航天大学出版社，1999.

［2］荆武兴，崔乃刚.基于高动态GPS接受机输出数据的卫星自主导航［J］.中国空间科学技术， 2000，20(6):23－29.

［3］黄翔宇，荆武兴.基于日－地－月信息的卫星自主导航技术研究［J］.哈尔滨工业大学学报， 2002，34(5):643 － 646，683.

［4］刘玉梅.基于小样本数据的航天器自主导航方法及其DSP实现研究［D］.哈尔滨:哈尔滨工业大学.2006.

［5］杨博，伍小洁，房建成.一种用星敏感器自主定位方法的精度分析［J］.航天控制，2001(1):12－16.

［6］郑洲顺，普乐.非线性最小二乘问题的一种迭代解法［J］.数学理论与应用， 2002，22(1):43 －45.

［7］WANG Dong，ZHOU Donghua，JIN Yihui.An extended nonlinear state predictor for a class of nonlinear time delay systems［J］.Progress in Natural Science， 2004，14(2):145－151.

Autonomous navigation method for multi-satellites mission

QIAN Ying－jing，JING Wu－xing，GAO Chang－sheng

(Dept.of Astronautic Engineering，Harbin Institute of Technology，Harbin 150001，China，qianyingjing@yahoo.com.cn)

In this paper，the autonomous navigation method based on the earth sensor and the star sensor on passive section during the multi－satellites mission is studied.The orbit prediction is given by the initial state which is determined by least square method.Digital simulations are conducted to analyze the influence of sampling period，measured arc length，accuracy of measurement，reference star positions and installation errors on the position accuracy.It is indicated that the effect of measuring errors is greater than the installation errors.

multi－satellites mission;autonomous navigation;least square method

V412.4+1

A

0367－6234(2010)05－0705－05

2009－04－01.

钱霙婧(1984—)，女，硕士研究生;

荆武兴(1965— )，男，教授，博士生导师.

(编辑 张 红)