H.264标准压缩视频的超分辨率重建

黄 哲，陈 浩，张 晔

(1.哈尔滨工业大学图像与信息技术研究所，哈尔滨 150001，huangzhe.hit@gmail.com;2.北京宇航系统工程研究所，北京 100076)

H.264标准压缩视频的超分辨率重建

黄 哲1，2，陈 浩1，张 晔1

(1.哈尔滨工业大学图像与信息技术研究所，哈尔滨 150001，huangzhe.hit@gmail.com;2.北京宇航系统工程研究所，北京 100076)

为利用低分辨率压缩图像序列来重建高分辨率图像序列，提出一种在凸集投影(POCS)方法框架下基于整数DCT域量化噪声模型的针对H.264标准压缩视频的超分辨率重建方法.首先建立压缩视频的降质退化模型，然后根据H.264标准中的整数DCT变换和量化过程建立整数DCT域的量化噪声模型，最后在凸集投影算法的框架下给出了基于整数DCT域量化噪声的超分辨率重建算法.实验表明该算法的超分辨率重建结果的主观质量提高明显，峰值信噪比可达到30 dB，一般迭代5次即可得到良好结果，算法复杂度较低.

超分辨率重建;整数DCT变换;量化噪声;H.264压缩视频

图像超分辨率重建是指利用一系列低分辨率图像来恢复原始高分辨率图像的重建过程.基于多帧图像的超分辨率算法最早由Tsai和Huang［1］提出;Stark［2］和 Petti［3］等将凸集投影(POCS)理论应用到图像超分辨率重建当中;Schultz和Stevenson［4］建立了基于最大后验概率(MAP)准则的超分辨率重建方法.这些方法在解决传统图像超分辨率重建问题时都取得良好的效果.

因原始视频的数据量十分庞大而难于存储和应用，所以压缩视频成为视频在应用中的主要形式，也形成了多种视频压缩标准，如MPEG和H.26X系列标准等.压缩过程势必引入下采样、模糊和量化噪声等降质过程.为解决这些问题，提高压缩视频的还原质量，针对压缩视频的超分辨率重建逐渐成为研究热点.初期的研究将传统的超分辨率重建方法应用于压缩视频，但因没有考虑压缩过程的降质特点而存在诸多弊端［5－6］.后来涌现出很多针对压缩视频的超分辨率重建方法，如Gunturk［7］和 Segall［8］等提出在贝叶斯框架下的基于最大后验概率(MAP)准则的重建方法;Altunbasak和 Patti等［9－10］利用压缩过程中的量化噪声提出基于凸集投影(POCS)理论的重建方法.这些方法多数是针对以8×8 DCT变换为核心的MPEG等视频压缩标准.如今以4×4整数DCT变换为核心的H.264标准已逐渐成为主流，可针对H.264标准的超分辨率重建研究却很少.

本文充分考虑H.264标准的特点，首先建立视频在压缩过程中的降质模型;其次分析H.264标准中整数DCT变换和量化的特点，建立整数DCT域量化噪声模型;然后提出在凸集投影(POCS)理论框架下的整数DCT域压缩视频超分辨率重建算法;最后进行仿真实验，分析实验结果和算法性能.

1 模型的建立

1.1 压缩视频模型

研究如何利用压缩后的低分辨率序列来重建原始高分辨率序列的基础之一，就是建立高分辨率原始视频和低分辨率压缩视频的关系，即压缩视频模型.

本文将所有图像均用一维向量表示.原始大小为pM×pN的高分辨率图像用(p2MN)×1的向量f表示，其中p为伸缩因子;经过下采样、模糊等降质过程后得到大小为M×N的低分辨率图像用(MN)×1的向量g表示;将g压缩后得到大小为M×N的解压缩图像，用(MN)×1的向量表示;通过超分辨率重建算法得到大小为pM×pN的高分辨率重建图像，用(p2MN)×1的向量^f表示.可由压缩码流获得，所以压缩视频超分辨率重建就是一个利用低分辨率解压缩图像来恢复高分辨率重建图像^f的过程.

1.2 整数DCT变换和量化的噪声模型

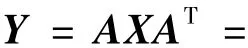
其中CfXCTf是二维正向变换核，Ef是尺度因子矩阵，符号⊗表示两个矩阵中的对应点相乘，d=c/b ≈ 0.41［11］.

H.264标准为在减少整数DCT变换环节中的非整数运算的同时保证变换的正交性，将b，c和d的值重新分配，就得到了最终的4×4整数DCT变换，即

上述整数DCT变换就是H.264编码器中采用的主要变换方式，是传统DCT变换的近似，在保证其正交性的同时拥有和传统DCT变换几乎一样的压缩性能，并避免了大量的非整数运算.其反变换为

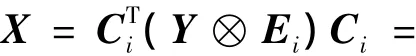
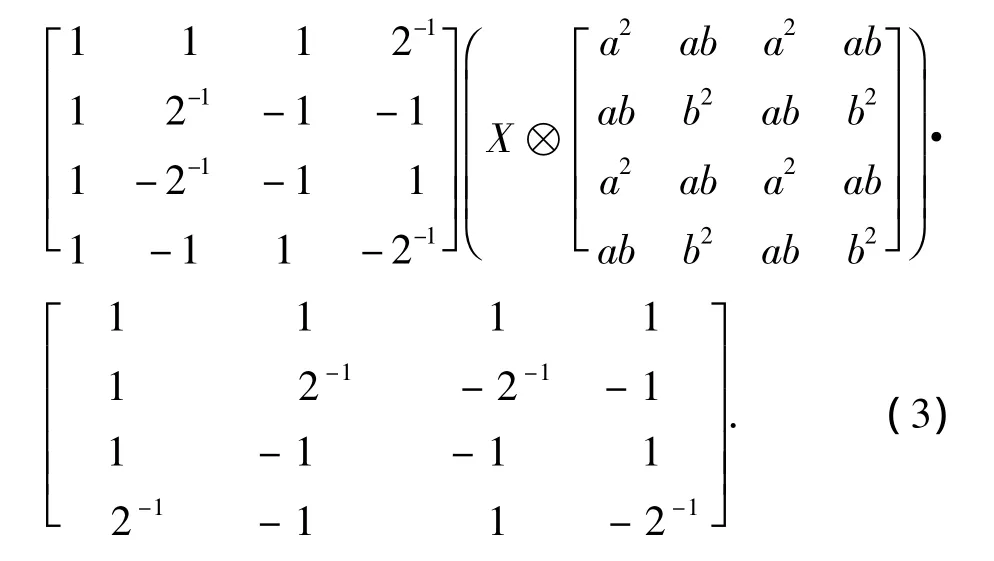
因为该变换是正交的，所以有如下关系:

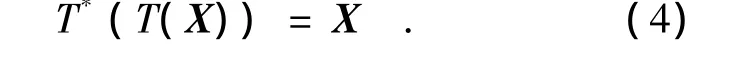
H.264标准中的量化部分采用的是尺度量化器，其基本的正向量化和反向量化分别为

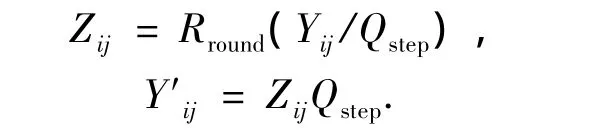
其中Yij是码块经过整数DCT变换后在系数矩阵Y中(i，j)处的系数;Y′ij是Zij经反向量化后得到的整数DCT系数矩阵Y′中(i，j)处的系数;Qstep为量化步长，由QP值决定，Rround函数表示取整操作.取整操作使量化后的结果丢弃了小数部分，在减少数据量的同时带来的后果是Y′ij≠Yij，造成了整数DCT系数的失真，即信息的丢失.这种信息的丢失，可以认为是在原有整数DCT系数上面加或者减去一个绝对值小于0.5Qstep的噪声，因此，用引入加性量化噪声Ndij的方式来表示，即:

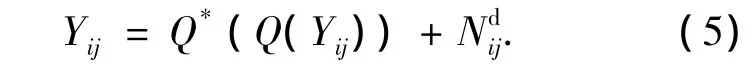
其中Ndij表示由于量化而引入到整数DCT域每个系数上的加性量化噪声.

由(4)和(5)得

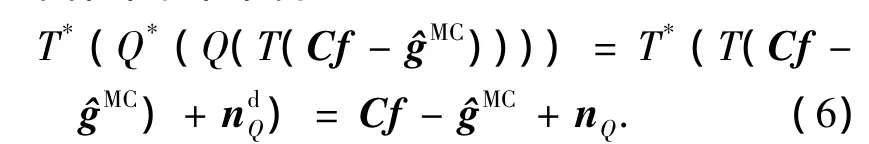
其中ndQ表示整数DCT域量化噪声的一维向量，nQ是表示空域量化噪声的一维向量，且ndQ=T(nQ).

将(6)带入(1)得

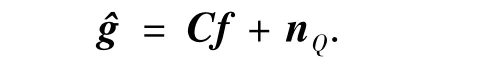
上述推导给出了整数DCT域和空域的量化噪声模型，以及原始高分辨图像和解压缩端得到的低分辨率图像的关系.可以看出压缩端的运动估计并不出现在原始高分辨图像和解压缩低分辨率图像的关系式中，因此本文将整数DCT域量化噪声降质模型作为后续超分辨率重建方法的基础.

将前文对码块矩阵的整数DCT变换和量化转换为对码块向量的操作.如果将码块矩阵X用16×1的一维向量x表示，整数DCT变换域系数矩阵Y用16×1的一维向量y表示，则(2)和(3)通过矩阵变换可以表示为

其中TDCT为16×16的整数DCT变换矩阵，TIDCT为16×16的反向整数DCT变换矩阵.

量化和反量化可以表示为

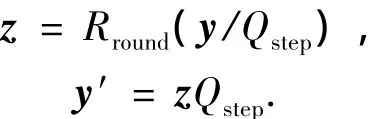
其中z为16×1的一维向量.

2 基于量化噪声模型的POCS超分辨率重建算法

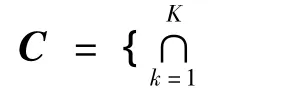
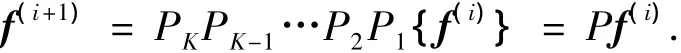
POCS算法中的初始值理论上可以是任意值，足够致密的有效解集中任意解都是可以接受的重建结果，但初始值和限制集的选择直接决定了算法的收敛速度和重建效果.下面，本文就根据前面的整数DCT域量化噪声模型推导限制集，并给出相应的投影算法来完成超分辨率重建.

2.1 基于量化噪声模型的限制凸集

下面来建立整数DCT域量化噪声模型的限制凸集.因为Rround函数表示四舍五入的取整操作，可以得出

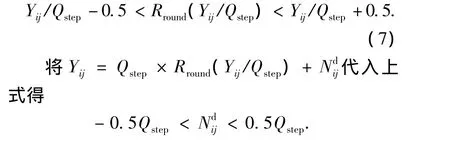
对于高分辨率原始图像f经过下采样后的低分辨率图像g=Cf和它的低分辨率解压缩图像来说，它们对应的4×4的码块都应该满足即g和在对应4×4码块上的差值经过整数DCT变换后每个变换域系数的值都在区间(－0.5Qstep，0.5Qstep)当中.式中(i，j)表示4 ×4码块在图像中的位置.

这样就可以构造一个如下的集合:

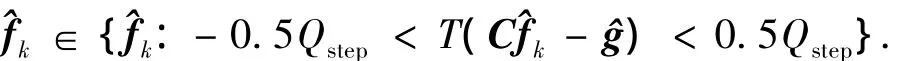
2.2 量化噪声模型的POCS算法

在文献［9－10］，［12］和［13］中提出的针对MPEG视频压缩标准中DCT变换及量化的凸集投影算法的基础上，利用前文建立的针对H.264标准的视频压缩模型和整数DCT域量化噪声模型，提出在凸集投影算法框架下的基于整数DCT域量化噪声限制集的压缩视频超分辨率重建算法，表达式如下:

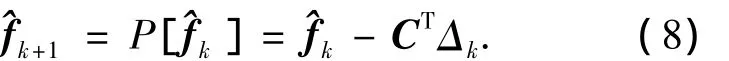
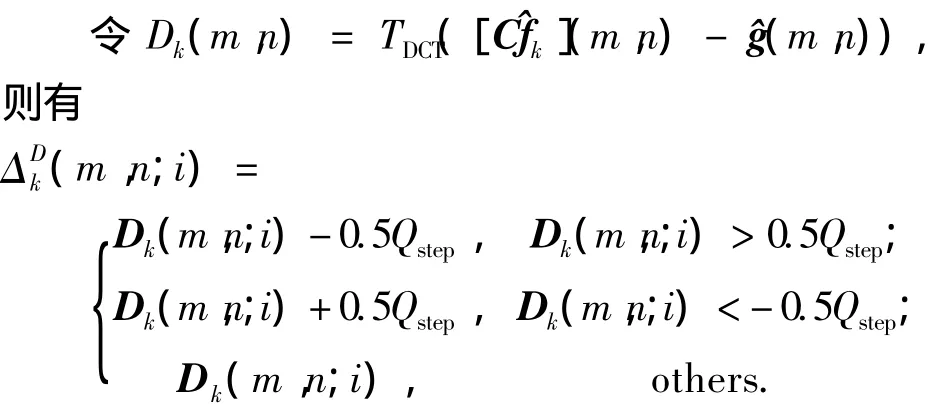
当每个码块对应的Δk(m，n)都已计算出来后就可得到Δk.在计算ΔDk(m，n)时，如果每一个Dk(m，n;i)(1≤i≤16)都在区间(－0.5Qstep，0.5Qstep)时，则放弃对这个码块的修正，保持其原始空域的值不变.通过上面的过程将Δk计算出后，就可以通过式(8)迭代计算出.当所有的Dk(m，n;i)都在区间(－ 0.5Qstep，0.5Qstep)时就停止迭代运算，此时的就是最后的超分辨率重建结果.迭代运算的起始值理论上可以设为空间中的任何一个向量，此处将低分辨率解压缩的图像的双线性插值图像作为，因为此方法一般得不到收敛的解，所以本算法认为经过若干次迭代之后，若^fk的质量不再明显变化时就停止迭代，此时的^fk就是超分辨率重建结果.

3 实验结果及分析

用实验来验证上述整数DCT域超分辨率重建方法的性能.首先，将CIF(352×288)大小的foreman序列中的一帧作为高分辨率原始图像，对其下采样得到4幅QCIF(176×144)大小的图像，并构成一个低分辨率序列.然后用JM8.6软件按照H.264标准的baseline档次，QP值设为 28，对上述低分辨率图像序列进行压缩，其中第1帧作为I帧，其他3帧为P帧，压缩比为27倍.解压缩后得到4帧低分辨率序列，对其中的一帧进行双线性插值得到一幅CIF大小的图像f0.以f0作为起始点利用上述算法进行迭代得到最终的重建结果，如图1所示，细节对比如图 2，对mobile序列与上述相同的实验，结果如图3所示.

上面的实验中重建结果的峰值信噪比(RPSN)相比双线性插值算法有很大的提高，可以达到30 dB以上.同样，重建结果相比双线性插值算法在信噪比(SNR)方面具有明显的优势，提升均在5 dB以上.同样可以看出视觉效果上细节信息更加丰富.同时本文算法通过较少迭代次数可得到稳定的重建结果，如图4所示，两组实验均迭代5次即可得到稳定的重建结果.对foreman序列在不同QP值下用JM8.6软件压缩并用本文算法进行重建，其结果相对于双线性插值算法重建结果的RPSN增量，如图5所示.而SNR的增量也有同样的趋势.因此得出本文算法在QP较小的情况下，具有更优的重建效果.采用分块操作尽可能化简了运算中矩阵和向量的大小，节省了计算时间和所需内存.

图1 foreman序列实验结果

图2 细节对比

图3 Mobile序列实验结果

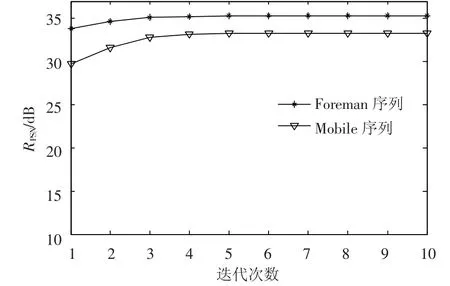
图4 RPSN随迭代次数变化曲线

综上所述，本文提出的基于整数DCT域量化噪声的压缩视频超分辨率重建方法在峰值信噪比和信噪比方面相比传统的插值算法有较大的提高，而且运算复杂度低，该算法中所使用的大量整数运算使其具有良好的优化前景.

4 结论与展望

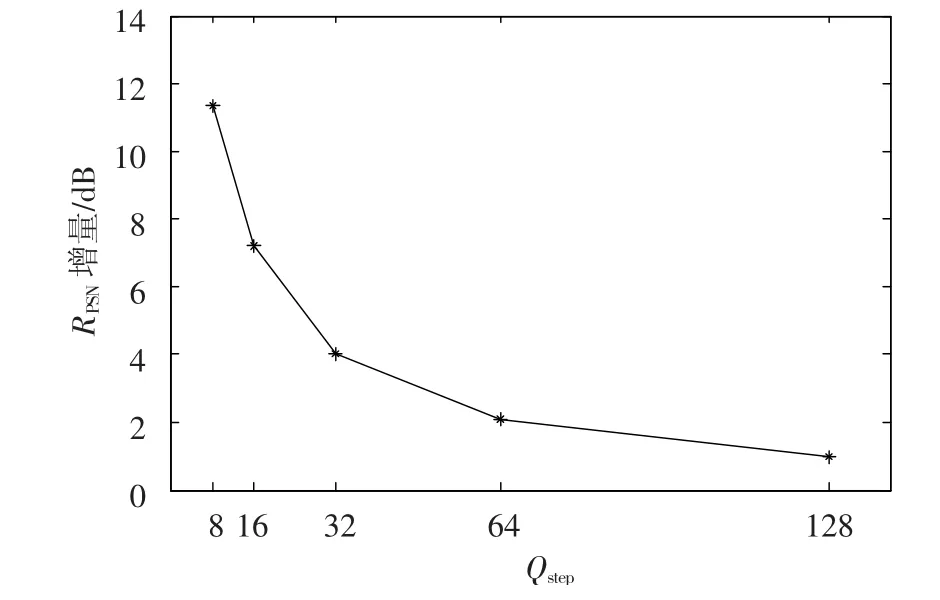
图5 RPSN增量与Qstep的关系

本文提出的基于整数DCT域量化噪声的压缩视频超分辨率重建方法，针对H.264标准的压缩视频拥有较好的主观重建效果，峰值信噪比较双线性插值等方法有较大提高，收敛速度较快，对计算机资源消耗较小.但本文的算法仍有很多局限性，例如只考虑量化噪声这一个压缩视频降质因素，并没有考虑由于预测和运动补偿等原因引起的降质过程;算法需要已知降质矩阵C，而通常这个矩阵也具有不确定性.在未来针对H.264标准的压缩视频超分辨研究当中，可以进一步引入运动补偿等降质模型;同时也可以根据整数DCT域量化噪声的统计模型建立在贝叶斯框架下的压缩视频超分辨算法.

［1］TSAI R，HUANG T.Advances in Computer Vision and Image Processing［M］.Greenwich:JAI Press Inc，1984:317－339.

［2］STARK H，OSKOUI P.High-resolution image recovery from image-plane arrays，using convex projections［J］.Journal of the Opt Soc of America， 1989，6(11):1715－1726.

［3］PATTI A J，SEZAN M I，TEKALP A M.Super-resolution video reconstruction with arbitrary sampling lattices and nonzero aperture time［J］.IEEE Trans on Image Processing， 1997，6(8):1064－1076.

［4］SCHULTZ R R，STEVENSON R L.Extraction of high resolution frames from video sequences［J］.IEEE Trans on Image Processing，1996(6):996－1001.

［5］SEGALL C A，MOLINA R，KATSAGGELOS A K.High-resolution images from low-resolution compressed video［J］.IEEE Signal Processing Magazine， 2003，20(3):37－48.

［6］徐忠强，朱秀昌.压缩视频超分辨率重建技术［J］.电子与信息学报， 2007，29(2):499－505.

［7］GUNTURK B K，ANTUNBASAK Y，MERSEREAU R.Bayesian resolution-enhancement framework for transform-coded video［C］//IEEE Int.Conf.Image Processing.Thessaloniki，Greece:［s.n.］，2001:444.

［8］SEGALL C A，KATSAGGELOS A K，MOLINA R，et al.Bayesian resolution enhancement of compressed video［J］.IEEE Trans on Image Processing， 2004，13(7):898－911.

［9］PATTI A J，ALTUNBASAK Y.Super-Resolution image estimation for transform coded video with application to MPEG［C］//IEEE International Conference on Image Processing.Kobe，Japan:［s.n.］，1999:179 －183.

［10］ALTUNBASAK Y，PATTI A J，MERSEREAU R M.Super-resolution stilland video reconstruction from MPEG coded video［J］.IEEE Trans.on Circuits and System for Video Technology， 2002，12(4):217 －226.

［11］RICHARDSON IAIN E G.H.264 and MPEG －4 Video Compression［M］.England:John Wiley and Sons Inc，2003:189－190.

［12］CHAUDHURI S.Super-Resolution Imaging［M］//SEGALL C A，KATSAGGELOS A K，MOLINA R.The International Series in Engineering and Computer Science.Norwell:Kluwer，2001:211 －242.

［13］胡辛.压缩图像超分辨重建算法研究［D］.西安:西安电子科技大学，2006:37－38.

Super-resolution reconstruction of H.264 compressed video

HUANG Zhe1，2，CHEN Hao1，ZHANG Ye1

(1.Institute of Image and Information Technology，Harbin Institute of Technology，Harbin 150001，China，huangzhe.hit@gmail.com;2.Beijing Institute of Astronautical Systems Engineering，Beijing 100076，China)

To reconstruct high-resolution(HR)images from a sequence of low-resolution(LR)compressed images，this paper proposes a novel algorithm focused on super-resolution reconstruction of H.264 compressed video，which is based on the integer DCT transform-domain quantization noise.Firstly，models of compressed video and integer DCT transform-domain quantization noise are surveyed.Then the reconstruction algorithm under the POCS theory is proposed.Experimental results demonstrate that this algorithm has a great improvement in subjective visual quality and low computation complexity，in which PSNR can reach 30 dB and iterations are less than 5 times.

super-resolution reconstruction;integer DCT;quantization noise;H.264 compressed video

TN911.73

A

0367－6234(2010)05－0721－06

2009－03－24.

黑龙江省自然科学基金资助项目(ZJG04－0701).

黄 哲(1983—)，男，硕士研究生;

张 晔(1960—)，男，教授，博士生导师.

book=42,ebook=95

(编辑 张 宏)