船舶振荡运动仿真的方向谱方法

赵振民，孔民秀，杜志江，孙立宁

(1.哈尔滨工业大学机器人与系统国家重点实验室，哈尔滨 150080，zhaozhenmin@sohu.com;2.黑龙江科技学院电气与信息工程学院，哈尔滨 150027)

船舶振荡运动仿真的方向谱方法

赵振民1，2，孔民秀1，杜志江1，孙立宁1

(1.哈尔滨工业大学机器人与系统国家重点实验室，哈尔滨 150080，zhaozhenmin@sohu.com;2.黑龙江科技学院电气与信息工程学院，哈尔滨 150027)

为了解决船舶振荡运动时域仿真和海浪与船舶运动一致性问题，提出了一种以频谱分析方法为基础，用方向谱代替海浪谱的船舶振荡运动计算方法.对海浪谱、方向谱进行数学描述和关系分析，并选择适合用于船舶振荡分析的长峰海浪谱和ITTC方向谱，根据Gerstner模型对海浪进行分解，建立了船舶在海浪中的振荡运动计算模型.采用响应振幅算子法描述遭遇波面与船舶运动的联系，根据线性叠加假设给出了船舶振动运动的时域解和频域解.

船舶仿真;海浪仿真;海浪谱;方向谱

从20世纪40年代起，研究人员开始致力于船舶振荡流体动力理论的建立.Haskind提出了在线性理论范围内将流场中的扰动速度势分解成绕射速度势和辐射速度势，该方法仍然是处理摇荡问题中线性扰动势的经典方法［1］.随着高速电子计算机的出现，船舶振荡运动理论也逐渐由二维理论发展到三维理论、由频域发展到时域、由线性假设发展到非线性处理［2－6］.

常见的频域分析方法都采用海浪谱描述随机海浪，很难以之为基础进行随机海浪上的船舶振荡运动时域仿真并使海浪和船舶振荡运动协调一致.为了解决该问题，本系统采用方向谱代替海浪谱进行频谱分析，建立基于方向谱的船舶振荡仿真系统，可以得到船舶运动和海面运动更加协调一致的效果.

1 海浪数学模型分析

1.1 海浪谱、方向谱及方向分布函数

根据Gerstner模型，海浪谱描述固定点的波面，因此只需要考察海浪场中一固定点的波面即

可.海浪高度场中一定点的一维高度表达式为

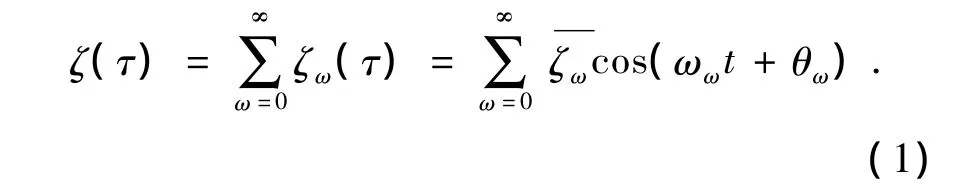
由式(1)规定

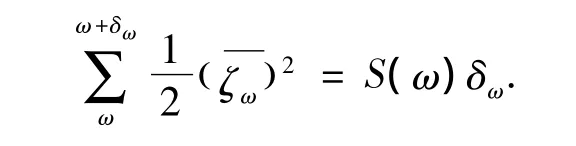
式中:S(ω)为海浪谱(称其表达式为海浪谱函数)，表示在频率ω附近单位频率范围内的组成波所具有的波动能量;方向谱描述海浪内部各个方向上的波面，因此对方向谱的研究必须从海浪场中任意点(x，y)的波面开始.根据Gerstner模型，海浪高度场中任意点(x，y)的高度表达式为

式中:χ为第ω号组成波的传播方向与x轴的夹角(浪向角)，ħω为第ω号组成波的波数，由频散关系 ωω= ω(ħω)确定.

由式(2)规定:

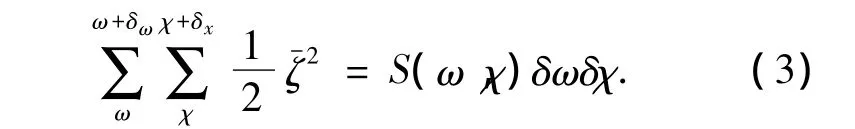
式中:S(ω，χ)为方向谱(称其表达式为方向谱函数)，它表示在浪向χ以及频率ω附近单位角度和频率范围内的组成波所具有的波动能量.

海浪谱与方向谱的关系为

则称D(ω，χ)为方向分布函数.

1.2 长峰海浪谱及ITTC的方向谱

如果海浪的组成波都相互平行，且它们的浪向都与海风的主风向相同，这种海浪就被称为长峰海浪.Pierson和Moscowitz从北大西洋的460组风浪观测资料中挑选出54组属于充分成长情形的数据，按照风速分组，并利用谱分析方法得到海浪谱函数:

式中:A=8.11 ×10－3g2;B 为0.74 g4/μwind4，μwind为海面上方19.5 m处的风速，该谱被称为Pierson-Moscowitz谱，简称P－M谱.

ITTC推荐的方向分布函数如下:

式中:α为组成海浪的方向χ与中心海浪χCW的夹角(本文简称浪向夹角);

将式(5)和式(6)代入式(4)，可得到基于P－M谱和ITTC方向分布函数的方向谱:

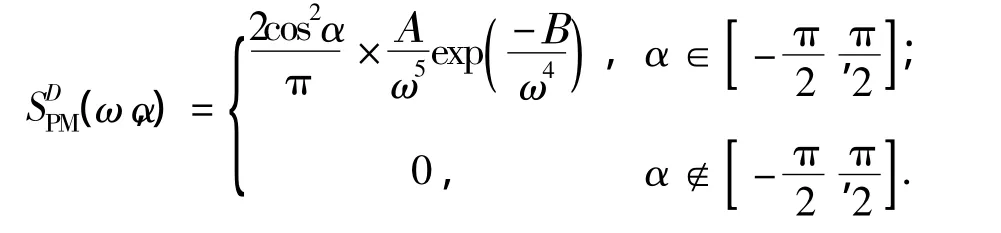
1.3 海浪的仿真

1)方向谱的选择.方向谱的选择直接影响仿真结果的质量，本文为了研究的通用性，选择最常用海浪谱方向分布函数构造了基于P－M谱和ITTC推荐方向分布函数的方向谱进行后续的计算.

2)海浪的分解.根据Gerstner模型的假设，海浪是由许多个规则波组成的，而海浪的分解就是要根据一定的原则得到这些规则波的分布.

当用方向谱描述海浪时，对海浪的分解需要从空间和频率两个方向进行.本文选择了先进行空间分解而后进行频率分解的顺序，它的含义是，总海浪由各个方向的子海浪组成，而每个子海浪又由各个频率段的规则组成波构成.本文出于简化的目的，在空间分解时采用了等角度法，在频率分解时采用了等频率法.

根据基于P－M谱和ITTC推荐方向分布函数的方向谱的特点，参考文献［7］，确定相应的频率仿真范围.本文只考虑风速对方向谱的影响，当风速确定后，每个子海浪的频率划分采用相同的方法.

2 海浪中船舶振荡运动数学模型分析

2.1 坐标系选取与各振荡运动量定义

在本文中采用3个坐标系描述船舶振荡运动.

1)惯性坐标系(O0－x0y0z0).该坐标系固定于海面，不随波浪或船体运动;其中O0－x0y0平面与静水面重合;通常是岸上的观测者所采用的坐标系，因此该坐标系是定义各物理量(航速、风速、方向谱等)的通用坐标系.

2)参考坐标系(O′－ x′y′z′). 该坐标系以船体前进的平均速度移动，但不随船体振荡;其坐标原点与船舶处于静水稳定时(既没有任何振荡运动时)的重心位置重合，x′轴指向船艏;该坐标系是定义各遭遇物理量(遭遇频率、遭遇海浪谱等)的坐标系;

3)动坐标系(O－xyz).该坐标系与船体固定，既以船体前进的平均速度移动，又随船体发生振荡运动;其坐标原点位于船舶的重心，x轴指向船艏;在其中描述的船体坐标是定值而不是时间的函数，同时也可以用此坐标系相对于参考坐标系的位置来定义船舶的振荡运动.

把船舶作为六自由度刚体，并利用动坐标系在参考坐标系中的相对位置定义各振荡运动分量(如图1).各运动量定义如下:动坐标原点O在参考坐标系中的纵坐标x′0称为纵荡，垂向坐标y′0称为垂荡，横坐标z′0称为横荡;绕动坐标系3个坐标轴的转动依次为横摇φ′0，纵摇θ′0和首摇ψ′0.在船舶振荡研究领域常常引入常量表示法来表示这6种振荡运动，其对应关系下式所示:

图1 船舶振荡运动的坐标系与船舶振荡运动的定义

2.2 遭遇频率与遭遇海浪谱

假设船舶以平均速度μship运动，且惯性坐标系的χ0正方向轴与船舶航向相同(见图2惯性坐标系部分，μship=0°).根据前面对惯性坐标系和参考坐标系的定义，得到两个坐标系的坐标变量间的关系:

将式(7)代入式(2)可得参考坐标系下的海浪波面表达式，即遭遇波面的表达式

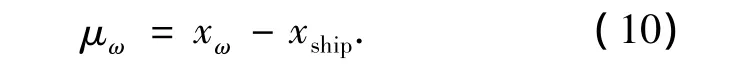
式中:μω为第ω号组成波在参考坐标系下的浪向，称为遭遇角.可以用组成波与船体运动正方向的夹角表示，规定顺时针为正，且当组成波与船体运动方向相同时为0°，具体参考图2.

图2 遭遇角μω以及船舶的航行状态的定义

式(8)～(10)中，t前的系数定义为船舶的遭遇频率，再考虑到无限水深条件下h=ω2/g(g是重力加速度，常取g=9.8 m/s2)，就可以得到遭遇频率和自然频率的数学关系为

根据式(11)由能量守恒定律可知，波面承载的能量是常数，不会因为坐标系的变化而发生改变，从而有如下海浪谱和遭遇海浪谱的关系:

2.3 遭遇海浪谱与船舶运动关系

在得到了遭遇海浪谱后，利用响应振幅算子以及遭遇海浪谱函数得到船舶运动谱函数，而后把描述规则波成分的参数带入船舶运动谱函数.

在进行基于方向谱的船舶振荡运动仿真时，海浪被分解为许多个不同浪向的子海浪，所以必须得到需要仿真的所有航速和所有子海浪的遭遇角下所有的响应振幅算子.根据文献［8］，响应振幅算子由振幅频率函数|RAO(ωe，μ，μship)|及相位频率函数φ(ωe，μ，μship)两部分组成，通常记为

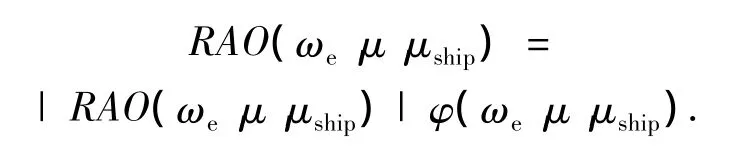
2.4 船舶振荡运动频域解

根据船舶运动响应的线性假设［8］，并且按照上述振幅响应算子的定义，船舶在一定海况中的振荡运动响应谱值可用下式计算［9］:

式(12)表示当遭遇角为μmain(即中心海浪的浪向为χCW而船舶航向为χship)且船舶航速为μship时，第i号运动的船舶振荡运动响应谱值为各组成波和船舶振荡运动响应相位值.

式(13)表示由第(i，j)号组成波所造成的船舶振荡运动响应谱值，第(i，j)号组成波是第i号子海浪中的第j号频率的组成波，而Sij(μi，ωj)是此组成波的方向谱值.方程中的M是响应振幅算子进行无量纲化时产生的系数，它的取值如下:当需要计算的自由度属于线位移时M= 1，角位移时M=ħ(ħ为波数)，力时M=1/c(c是回复力系数).式(14)表示当遭遇角为μmain(即中心海浪的浪向为χCW而船舶航向为χship)且船舶航速为μship时，第i号运动的船舶振荡运动响应相位为由该遭遇角μmain和船舶航速μship共同确定的相位频率函数值.需要指出的是，浪向χ、浪向夹角α和遭遇角μ之间的关系可以通过式(10)及式(6)唯一确定.

在大多数情况下浪向χ是最先获得也是最受关注的，所以，采用公式(15)～(18)这组公式计算船舶的振荡运动响应谱值.

2.5 船舶振荡运动时域解

与对海浪波面描述类似，船舶的振荡运动的描述也可以表示为许多组成运动的叠加［10］，基于线形假设，通常用三角函数的形式表达这些组成运动［11］，其表达式如下:

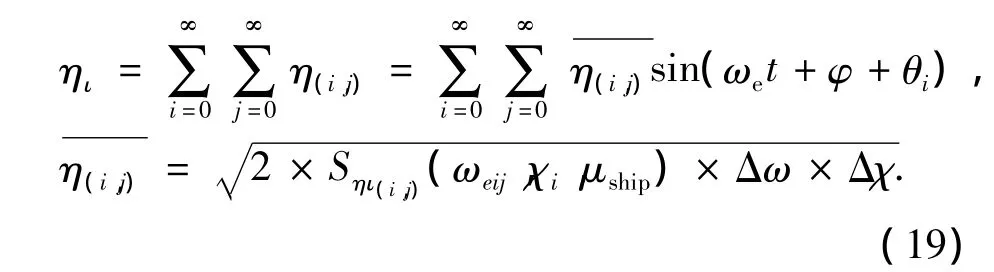
式中:ηl为自由度的位移，为自由度由第(i，j)号组成波造成的组成运动的振幅，ωe为自由度由第(i，j)号组成波造成的组成运动的遭遇频率，φ为自由度由第(i，j)号组成波造成的组成运动的随机相位，θi为自由度由第(i，j)号组成波造成的组成运动的响应振幅算子相位响应，第(i，j)号组成波是指第i号子海浪中的第j号频率的组成波.

3 结论

本文介绍了与本系统相关的数学模型和基于方向谱的船舶振荡分析方法.从这些数学模型中推导出的基于方向谱的船舶振荡分析方法以频谱分析方法为基础，通过把方向谱代替海浪谱得到了基于方向谱的船舶振荡运动分析方法，并以基于P－M谱和ITTC推荐的方向分布函数的方向谱为例完成了基于方向谱的船舶振荡运动分析.

［1］HASKIND M D.The oscillation of a ship in still water［J］.Prikladnaya Matematika I Mekhanika， 1946，10(1):33 －66.

［2］ZHOU Weilin，HUA Yi，YUN Liang.Nonlinear equations for coupled heave and pitch motions of surface effect ship in regular waves［C］//Proc of the Can Symp 14th Air Cushion Technology.Ottawa Ont Can:CASI，1980:327－359.

［3］ANDERSON P，WUZHOU H.On the calculation of two-dimensional added mass and damping coefficients by simple green＇s function technique［J］.Ocean Engineering， 1985，12(5):425－451.

［4］CHOU C R，WENG W K，YIM J Z.Ship motions near harbor caused by wave actions［J］.Computer Modeling in Ocean Engineering， 1991，12(1):443 －453.

［5］TAKAGI K，NAITO S.Hydrodynamic forces acting on a floating body in a harbor of arbitrary geometry［J］.International J of Offshore and Polar Engineering， 1994，4(1):97－104.

［6］DENIS S，PIERSON W J.On the motion of ships in confused seas［J］.Trans SNAME， 1953，61:71 －77.

［7］刘洁，邹北骥，周洁琼，等.基于海浪谱的Gerstner波浪模拟［J］.计算机工程与科学， 2006，28(2):20－23.

［8］LEWIS E V.Principles of Naval Architecture vol III:Motions in Waves and Controllability［M］.Second Revision.Jersey City，NJ:Society of Naval Architects＆Marine Engineer，1990:126 －137.

［9］KORVIN-KROUKOVSKY B V.Investigation of ship motions in regular waves［J］.Trans SNAME， 1955，63:91 －96.

［10］CHAPMAN R B.Large amplitude transient motion of two-dimensional floating bodies［J］.Journal of Ship Research， 1979，29(1):20－31.

［11］CHAPMAN R B.Time-domain method for computing forces and moments acting on three-dimensional surfacepiercing hull with forward speed［C］//3rdInternational Confon NumericalShip Hydrodynamics. Paris:［s.n.］，1981:237－248.

Simulation method for ship oscillation based on directional spectrum

ZHAO Zhen-min1，2，KONG Min-xiu1，DU Zhi-jiang1，SUN Li-ning1

(1.State Key Laboratory of Robotics and System，Harbin Institute of Technology，Harbin 150080，China;2.College of Electric and Information Engineering，Heilongjiang Institute of Science and Technology，Harbin 150027，China)

To solve the problems of the simulation in time domain and the consistent movement between waves and ships，based on frequency-spectrum analysis method，a novel method for calculating the ship oscillation movement is proposed，in which directional spectrum is used instead of using ocean wave spectrum.Mathematic expressions and the relationship between wave spectrum and directional spectrum are introduced and the long-crested wave spectrum and ITTC directional spectrum suitable for ship oscillation movement analysis are selected.The ocean wave is decomposed using Gerstner model，and then the simulation model of ship movement in the waves is built.The relationship between encounter wave surface and ship movement is described by response amplitude operator method.With the linear superposition assumption，the results of ship oscillation movements in frequency domain and time domain are obtained.

ship simulation;ocean wave simulation;ocean wave spectrum;directional spectrum

TP391.9

A

0367－6234(2010)05－0742－04

2009－12－26.

国家高技术研究发展计划资助项目(2006AA040103).

赵振民(1967—)，男，博士研究生;

孙立宁(1963—)，男，教授，博士生导师.

(编辑 杨 波)