CGF智能决策模型中的威胁评估方法研究

李 峥，李照顺

（海军指挥学院，江苏 南京211800）

高技术海战中，执行各种作战任务的水面舰艇面临着越来越严重的空中威胁，对空防御已成为水面舰艇防御的首要任务。对来袭空中目标（主要是指反舰导弹、轰炸机和攻击机等）的有效防御是建立在及时而准确的威胁判断基础之上的，只有对空中目标构成的威胁度作出及时正确的判断，才能够合理分配抗击的兵力兵器，合理确定抗击的次序，使防御的综合效益最高。在海战CGF智能决策系统中，对目标的威胁判断是行为决策的关键任务之一。战场环境中有很多复杂不确定的因素影响目标的威胁评估。现有包括模糊集理论在内的很多方法用于威胁评估中，能增强行为模型的逼真度。

1 威胁评估方法

威胁判断受来袭空中目标的性质、类型、攻击能力以及目标距离、速度和舷角等诸多因素的影响。由于空中态势复杂多变，使得这些因素都具有不确定性和模糊性。目前，对空中目标威胁判断常用的层次分析法[1]主观性太强，而支持向量机[2]（SVM）的方法其核函数选取困难且精度不高，模糊集理论由于在解决不确定性和模糊性问题方面所具有的优越性，而成为威胁判断研究的良好工具。该方法可以更好地解决CGF智能决策系统中面临不完整的态势感知和不确定性信息时的威胁评估问题。

2 威胁因素分析

多个目标产生的威胁等级，实际上取决于多个不同的因素。美国仿真训练实验室[3]（IST）对此开展了大量的研究工作：一些与战场态势相关，如天气情况、地理环境、敌、我、友军队的兵力部署及战斗力等，还有一些涉及到所分析目标的特征，如编队信息、射击状态等。在CGF行为决策模型中，进行威胁估计通常考虑的因素主要有：聚合级威胁评估、近程防御、目标的有效射程、目标的射击状态、视线角、目标的相对高程、目标的机动、目标类型、射击扇面等[4]。

2.1 聚合级威胁评估

随着分布交互仿真规模的不断扩大，平台级实体越来越无法满足要求。将一定规模的作战实体聚合起来，通过对聚合级实体的作战行为进行足够的建模，将有效地解决平台级实体仿真中出现的规模小、模型复杂、网络负载大等问题。聚合级实体中的目标，若属于一个具有威胁的聚合级实体则其威胁度更高。因此，主要考虑以下威胁因素：

1）编队类型信息。由于不同类型编队的武器装备和舰艇平台性能是不同的，目标的攻击方式、攻击威力等都不同，因此，其威胁度也不相同。

2）目标距离。由于火力打击距离有限，目标距离也是影响打击决心的因素之一；同时，目标愈近，相对威胁度也愈大；所以应优选距离较近、在火力打击范围之内的目标。

3）目标航向。通过对目标航向的观察，可大致推测海上目标之意图。敌奔我而来，则敌进攻意图明显；敌背我而去，则敌逃跑意图明显。由此可见，目标航向不同，对指挥员决定打击决心的影响亦不同。

4）目标航速。航速是衡量目标机动性能的重要指标之一，也是目标重要属性之一。不同的目标具有不同的作战速度，即使是同一海上目标，速度不同，其威胁度也有所不同。一般认为，目标的速度越快，其威胁度越大。

5）瞄准状态。指目标武器系统的攻击状态，即是否正确瞄准所要打击的目标。

6）机动性。目标抗机动能力越强，越能影响对目标实施打击的火力，对目标杀伤概率及战果也会相应下降，相应威胁度也增大。目标的机动性能大大提高了其突防能力和命中概率。

7）锁定目标概率，取决于装备在目标上的电子战探测设备效能。

2.2 近程防御

如果当前战场态势中存在能同样打击目标的友方实体，那么目标的威胁等级就会降低，但要保证始终大于0。

2.3 目标的有效射程

如果平台在目标的火力打击范围内，那么其威胁等级会增加。为模拟出这种武器的射程，根据该武器的有效射程和最大射程建立一组和威胁等级相对应的四个射程范围，分别定义为：最小范围、边界范围、杀伤范围和致命范围。

2.4 目标的射击状态

目标的状态直接影响其威胁等级。涉及这一因素的主要有四个子因素：

1) 目标正处在开火状态；

2) 目标正瞄准平台；

3) 目标已经射击完毕；

4) 目标正在处于搜索阶段。

2.5 视线角

这一因素表示了飞行器的跟踪方向，只有飞行器要考虑这一因素。如果目标跃升攻击将增加目标的威胁等级。

2.6 目标的相对高程

作战想定中海拔的高低可能会影响威胁等级。表示这一因素的模糊集的值为：低于海平面、高于海平面、远远高于海平面。

2.7 目标的机动

这一动态因素能预测出驶向平台的目标是否变得更具威胁。

2.8 目标类型

目标类型直接影响威胁等级。然而为此，目标类型需要提前定义。如果目标类型不能确定，那么就必须用其它方式预测出它的类型或者为了保险起见将默认的威胁等级设置为最高。

2.9 射击扇面

作战单元搜索目标的扫描扇区称为射击扇面。如果平台在射击扇面内，那么目标的威胁等级将会增加。

3 威胁等级的计算

在测量和评估以上因素时考虑到固有的不确定性和模糊性，可以利用模糊集理论[5]来表示。

3.1 集合的定义

设 X，Y是两个有限集，X表示影响威胁度 Th的因素集，由以上分析的威胁因素构成。Y表示威胁度的有限集合。对定性的属性采用G.A.Miller的9级量化理论进行量化，并进行归一化处理；对定量属性采用区间量化，并对其进行归一化处理。定性属性的量化值和定量属性的量化区间通常要通过专家群组决策来确定。例如，Y = {0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6,0.7,0.8, 0.9, 1}分别表示威胁程度极小、非常小、较小、小、中大、较大、非常大、极大。R表示X到Y的模糊关系。模糊关系R通常用区间[0,1]中的系数构成的矩阵表示，R(x,y)表示有序对(x,y)具有关系R的程度。

设A和Th分别表示X和Y的模糊关系函数。定义运算符◊，对所有的y∈Y，有：

注意到A◊R是Y的模糊子集。此外，由对运算符◊的定义可知，[A◊R](y)表示着Th等于y。根据Sup-min运算并且在图1中可以直观地看出来。如图1所示，y与A之间链路的权重等于最小链路的模糊关系值（min运算）。y与A之间的关系隶属度等于所有链路权重中最大的链路权重值（Sup运算）。因此，对于所有的y∈Y，Th(y)= [A◊R](y)，简化记为：

图1 ◊运算图释

针对一个目标，给出模糊关系R和对应隶属度A的集合，方程(1)可以计算出威胁度Th。反过来，给定某一目标的威胁度和隶属度A的集合，解方程可以得出R。方程(1)的解可能不唯一，即给定一组A和Th，不只一种关系集合满足方程。然而满足方程(1)的最大模糊关系集被定义[6]为：

这里，φ是定义在[0,1]的模糊蕴涵运算符：

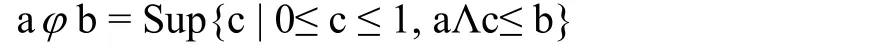
通过方程（2）可以得到A和Th之间满足方程（1）的最大模糊关系集关系集R也能作为A和Th之间模糊推理集。

3.2 估计最大的模糊关系集

对于给定目标的隶属度A的集合和A与Th之间的模糊关系R，建立了计算威胁度Th的方程（方程（1））。由方程（2）就可以得到A和Th之间满足方程（1）的最大模糊关系集。为了能得到模糊关系R，从而给定目标属性值就能计算或估计出它的威胁度，需要在某一属性集与Th值之间建立对应关系。这一估计问题可以描述为：

对于一组模糊集合对(A1,Th1),……,（AN,ThN），估计出R使得方程对所有的K=1,2,…,N，都满足：

给定的集合对看作训练集合，根据它估计出关系集R。如果设计适当的训练集合，就可以由给定的目标属性集合A估计出任意目标的威胁度。

方程（3）中每个独立的方程对应方程（2）最大的解可能不只一种。令ℜk为满足第K个方程的关系集：

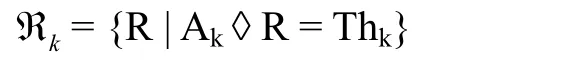
如果：

通过把所有满足各个独立方程的最大模糊关系相交，可以算出满足方程的最大的解，即

由实践得知：判断条件（4）通常比较困难，因此常采取以下步骤估计出关系集R。

3.3 算例分析

为了举例说明上述算法，简化起见，对X,Y做如下定义：

其中，X表示影响Th的属性，包括如下属性：聚合级威胁评估（ATA）、近程防御（NCT）、目标的有效射程（TER）、目标的射击状态（TFS）。Y表示威胁度集合，分别表示威胁程度极小、较小、小、较大、非常大、极大。

用向量矩阵表示模糊集A和Th，按集合X,Y的顺序隐含表示。如A = {0.9/ATA, 0.1/NCT, 0.8/TER,0.4/TFS}，可记作A = [0.9, 0.1, 0.8, 0.4]。为了简化说明，设训练集合由如下两组模糊集组成：

由方程(1)得：

同理得到：

交叉相乘得：

例如,

3.4 估算最大的模糊关系

基于上述算法的大量试验表明，在很多情况下，步骤2)算法中得到的最大关系集不能满足方程，但得到的Th的值与训练集中的初始值很接近。在一些情况下，如果由关系值得到的Th值在由训练集提供的初始值的范围内，近似解也是可以接受的。用ε表示由Th决定的关系值允许的误差范围。在步骤3)算法的基础上扩展，由给定的训练集可以得到一个近似解。

3) 如果(distance(Thk, [Ak◊R])≤ε)对所有的k=1,2,3,…N都成立，那么是近似解。

4 结束语

本文对CGF智能决策模型中目标的威胁因素进行了具体分析，阐述了利用模糊关系方程算法进行威胁评估，并通过实例计算给出了实践中估算最大模糊关系的方法。例如，美国Loral公司为SIMNET开发的ModSAF计算机生成兵力系统[7]就利用了这种算法建立了威胁等级和影响因素之间的模糊关系，并以此通过给定的影响因素估计出目标的威胁等级。结果表明，该方法能满足CGF决策模型的需求，增强了CGF仿真系统的精度和逼真度。

[1]宋国春,刘忠,黄金才.AHP方法的敌地域通信网通信链路威胁评估[J].火力与指挥控制,2008,33(2):16-20.

[2]黄现江,余思明.基于修正核函数的支持向量机空袭目标威胁评估[J].指挥控制与仿真,2009,31(6):33-35.

[3]郭齐胜.计算机生成兵力导论[M].北京:国防工业出版社,2006.

[4]葛恩顺,包磊.基于模糊理论海上目标威胁评估的改进算法[J].舰船电子对抗，2009,31(6):44-47.

[5]刘林.应用模糊数学[M].西安：陕西科学技术出版社,2008.

[6]Pedrycz W..Gomide fd.An Introduction to Fuzzy Sets Analysis and Design[M].MIT Press, Cambridge,Massachusetts, 1998.

[7]庞国峰.分布式虚拟战场环境中计算机生成兵力系统的研究[D].北京:北京航天航空大学,2000:6-9.