基于GRNN网络的燃气轮机可靠性预测研究

曲成家，刘永葆，贺 星

(海军工程大学 船舶与动力学院，湖北 武汉430033)

1 引言

可靠性预测是在设计阶段进行定量预估未来产品可靠性的一种方法。如果说可靠性分配[1]是从系统到单元、由整体到个体来进行的话，那么可靠性预测则是按相反的方法进行。可靠性预测常常作为可靠性分配的基础，两者关系密切，都是可靠性设计的重要环节。

燃气轮机的研制涉及气动、热力、燃烧、材料、结构、控制和机械加工等多学科技术，是知识密集、技术密集和资金密集的结晶，其可靠性是一个重要的性能指标。但由于其结构及功能复杂、启停频繁、运行工况多变、受环境影响大，所以依靠传统的可靠性定量计算来衡量燃气轮机的可靠性具有一定的局限性，甚至所得结果与实际结果相差甚远。

运用已往的工程经验与故障数据，结合当前的技术水平，来预测燃气轮机实际可能达到的可靠度，即预测其在特定应用中完成规定功能的概率。这对分析评估燃气轮机的可靠性水平、了解燃气轮机设计和研制中的薄弱环节、指导制造厂家更好地开展设计分析和改进工作具有重要作用。

可靠性预测有许多方法，如回归预测法、修正系数法、相似产品类比论证法等。但这些方法对带有时序特征呈高度非线性的可靠性数据的处理，其精度往往不高。而神经网络能实现从输入到输出状态空间的高度非线性映射[2]，故本文采用神经网络来进行可靠性预测。

2 燃气轮机可靠性预测数学模型

已知燃气轮机在故障时间序列t1，t2，…，tn时刻的可靠性历史统计数据，预测其下一时刻tn+1的可靠度，其数学模型可表述为[3]：

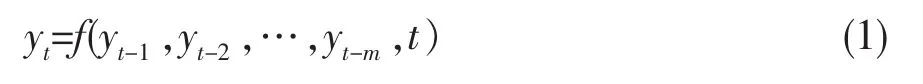
这类预测问题的关键是确定函数关系f，一般可用一元或多元线性回归方法将历史数据拟合成一个显式表达式。此方法虽然简单易行，但对于高度非线性问题，其拟合精度往往难以保证。而人工神经网络却能实现从输入到输出状态空间的高度非线性映射，可用来解决上述可靠性预测问题。

在燃气轮机的各种可靠性指标中，由于其启动过程的复杂性、启动程序的严格性，所以对其启动可靠性有着较高的要求。根据实际运行数据，利用神经网络较好的高度非线性映射性能，来预测和研究各型燃气轮机的实际可靠度有着重要的意义。

为了对某型燃气轮机实际运行的可靠性进行预测，对该型燃气轮机启动过程中发生的故障事件进行了统计。表1列出了前20台次该型燃气轮机发生启动故障时的累计工作时间及台次数，此前累计启动次数为1 583次。

3 神经网络模型及其优化设计

从神经网络函数逼近功能这个角度来分，神经网络可以分为全局逼近网络和局部逼近网络[4]。BP网络(后传播网络)是全局逼近网络的典型例子，但BP网络对于每个样本即输入输出数据对，网络的每个连接权均需进行调整，从而导致全局逼近网络学习速度变慢。而局部逼近网络则只需对网络输入空间某个局部区域的少量连接权进行调整，从而具有学习速度快的特点。目前常用的局部逼近神经网络有 CMAC 网络、径向基函数(RBF)网络[5～8]和 B 样条网络等。而广义回归神经网络(GRNN网络)[9]是径向基网络的一种变化形式，训练速度快，非线性映射能力强，故本文选用GRNN网络进行燃气轮机可靠性预测。

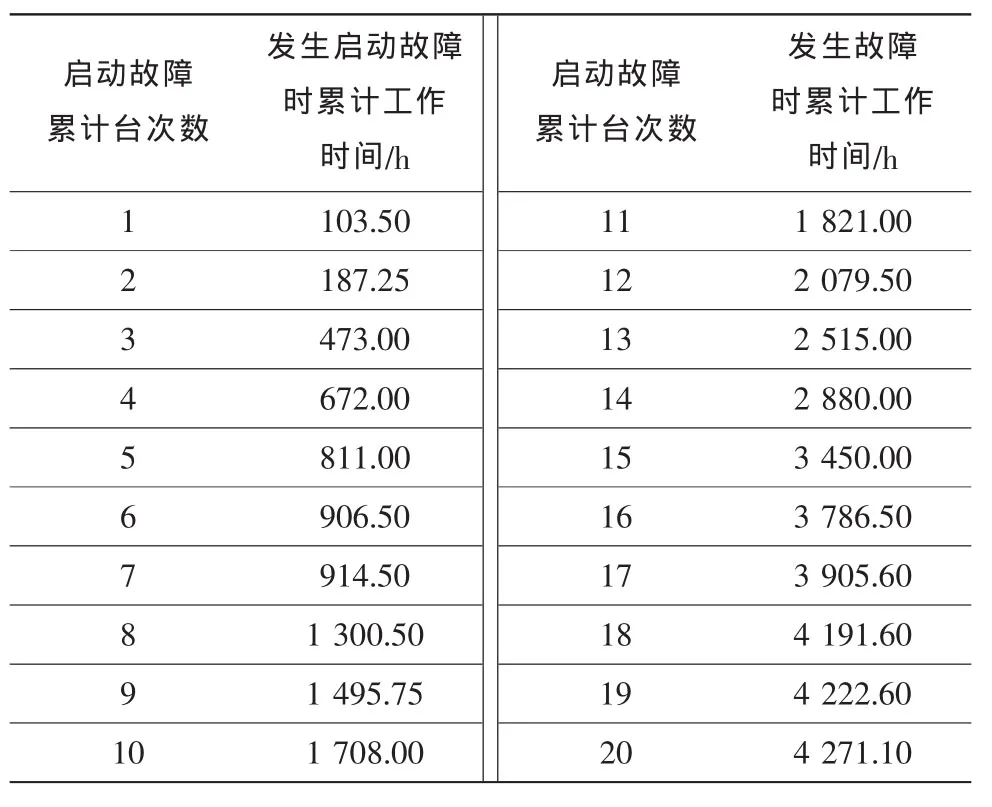
表1 某型燃气轮机发生启动故障时的累计工作时间及台次数Table 1 Total operating time and number of gas turbine for starting fault

3.1 GRNN网络基本结构与算法

GRNN网络由一个径向基网络层和一个线性网络层组成[10～12]，网络结构如图1所示。P表示输入向量，R表示输入维数，Q表示每层网络中的神经元个数，同时也表示训练样本的个数。

网络的第一层为径向基隐含层，单元个数等于训练样本数Q，该层的权值函数为欧几里德距离度量函数(用‖dist‖表示)，其作用是计算网络输入与第一层的权值IW1，1之间的距离，b1为隐含层阈值。符号“·*”表示‖dist‖的输出与阈值b1的元素与元素之间的乘积关系，并将结果形成净输入n1传送到传递函数。隐含层的传递函数为径向基函数，常用高斯函数作为网络的传递函数，式中σi决定第i个隐含层位置处基函数的形状，σi越大则基函数越平缓，故称为光滑因子，又被称为分布密度SPREAD。

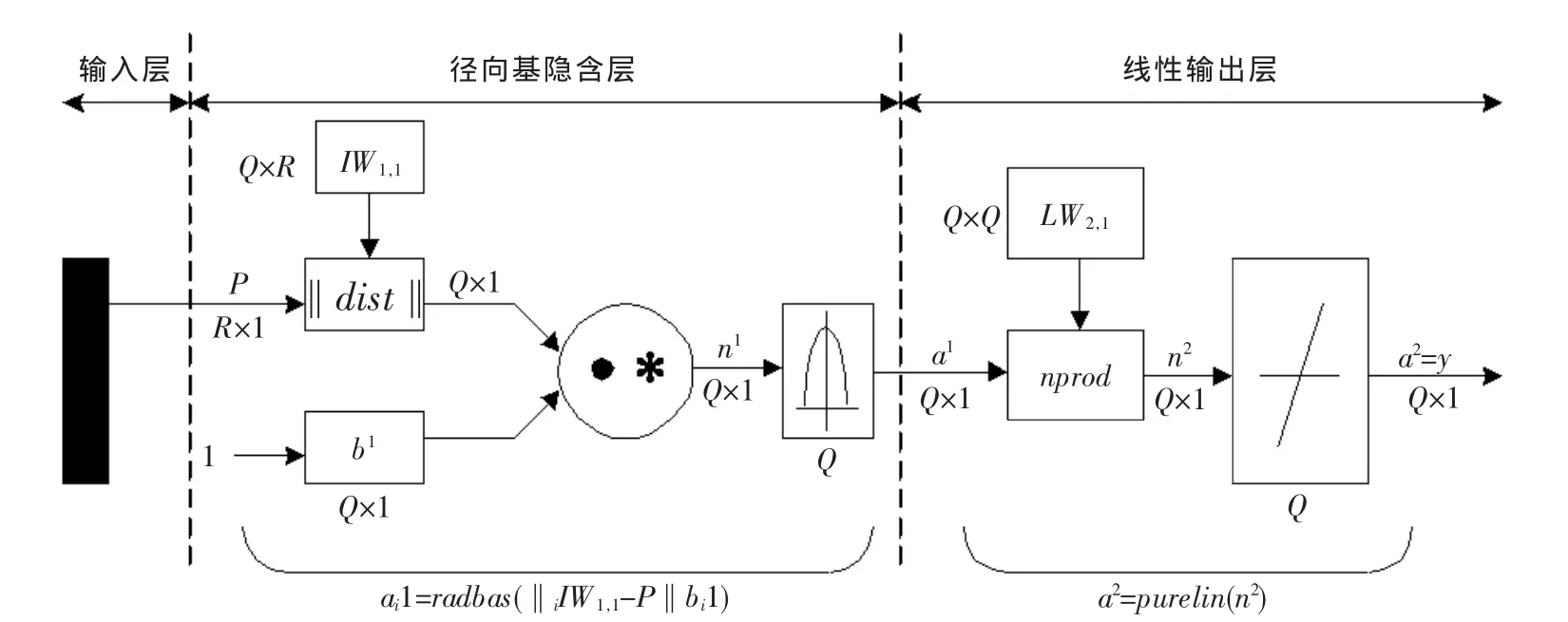
图1 GRNN网络结构图Fig.1 The structure of GRNN

网络的第二层为线性输出层，其权函数为规范化点积权函数(用nprod表示)，计算出网络的向量n2，它的每个元素就是向量a1与权值矩阵LW2，1每行元素的点积再除以向量a1各元素之和的值，并将结果n2送入线性传递函数a2=purelin(n2)，计算网络输出。

3.2 神经网络优化设计

GRNN网络的第一层与函数newrbe()设计网络的原理相同，其神经元的数目与输入期望值样本向量对的数目相等，第一层的阈值为0.832 6/SPREAD的列向量。选择SPREAD的原则是使得第一层输入向量与神经元权值向量之间的距离为0.5。第一层神经元的网络输入为加权输入与相应阈值的乘积，然后通过神经元函数radbas()计算得到第一层神经元的网络输出。GRNN网络第二层的神经元数目同样与输入期望值样本向量对的数目相等，此时其权值设定为期望值。在GRNN网络的设计中，SPREAD越大，拟合函数就越平滑，但SPREAD的大小会影响预报误差。所以在SPREAD的选择上要根据平滑度和误差来合理折中选取。

同时，为了对比，也用BP网络进行了计算机算法实现。BP网络设计中的关键就是隐层数的设计，而隐层的神经元数目选择十分复杂，往往需要根据设计者的经验和多次试验来确定，因而不能用一个理想的解析式来表示。隐单元数目与问题的要求、输入/输出单元数目都直接相关。隐单元数目太多会导致学习时间过长、而误差不一定最佳，也会导致容错性差、不能识别以前没有看到的样本，因此存在一个最佳的隐单元数。式(2)～式(4)可用作选择最佳隐单元数时的参考公式[13]。

式中：k为样本数，n1为隐单元数，n为输入单元数。如果

式中：m为输出单元数；a为调节常数，且在1～10之间取值。

另外，结合作者的实际使用经验，当n1在式(5)范围内选取时可得到较佳的效果。

4 算法实现及结果分析

首先把表1中的实际数据转换为网络的学习样本。根据式(1)所示预测模型对故障数据进行如下处理：以t时刻的可靠度Rt作为函数的输出，以t时刻之前的t-1、t-2、…、t-m这m个时刻的可靠度Rt-1，Rt-2，…，Rt-m以及时刻 t作为输入变量，构成式(6)的函数关系：

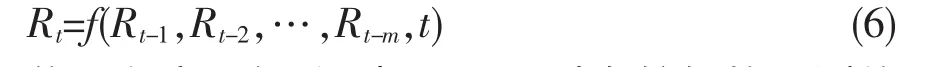
依工程实际经验，当m取5时有较好的预测效果。根据表1中的数据，结合式(6)以及BP网络的要求，将其转换为BP网络的15组训练样本，见表2。

其次是获得样本数据向量。由于其中各个指标存在相同，原始样本中各向量的数量级差别很大，为了计算方便及防止部分神经元达到过饱和状态，在研究中，对样本的输入向量中超出[-1，1]的向量进行归一化预处理[13]。设第j列需要归一化处理，归一化公式为：

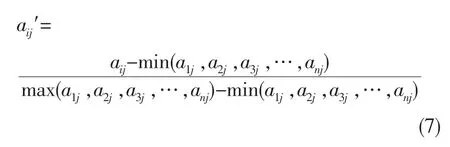
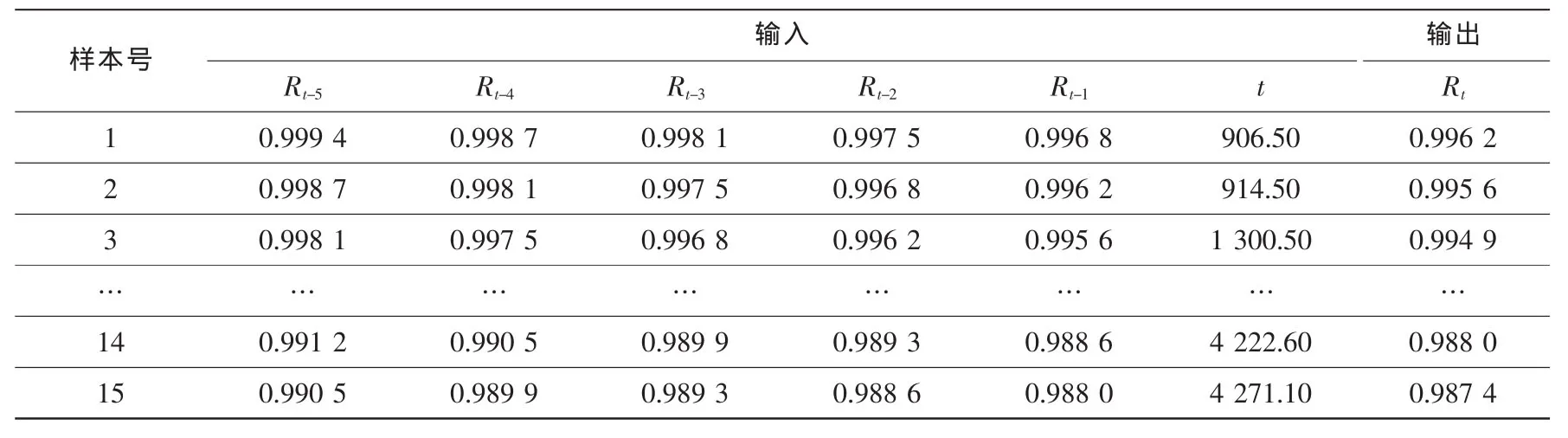
表2 网络的学习样本Table 2 Learning samples of neural network

本文样本中发生启动故障时的累计工作时间t就要进行归一化预处理。

根据上节中阐述的神经网络优化设计，本文分别用BP网络和GRNN网络进行了算法的计算机实现。为了对比各种参数对训练结果的影响，进行了各种参数的训练试验，其结果见图2～图5。

由图2可以看出，在本文的BP网络设计中，隐层单元数为13时对样本训练100次后的误差为1.118 59×10-11，效果比隐层单元数为3、20和35时的都要好。而文献[3]中利用与本文相同输入单元数的样本训练9 971次后误差平方和才下降到0.005，其原因是中间层神经节点数(隐层单元数)选取过大(为 80)所致。

从图3中可知，当SPREAD=1×10-5时，GRNN网络在算法实现中其训练用时比BP网络要少，而精度要比最佳的BP网络(隐层单元数为13)训练100次后达到的精度要高。

从图4中由GRNN网络得到的预测值和真实值的比较可以看出，真实值和预测值完全重合，这是因为测试数据就是训练数据。

图5是根据样本训练好的GRNN网络对下一时刻燃气轮机启动可靠性的预测。选择对燃气轮机将要运行到4 500 h时刻的启动可靠度进行网络预测模拟，结果表明，预测值为0.986 9，而参考值(即假设该时刻发生启动失败时的燃气轮机可靠度)为0.986 7，预测值大于参考值，故可以认为在运行到4 500 h时刻之前，该型燃气轮机不会发生启动失败故障。

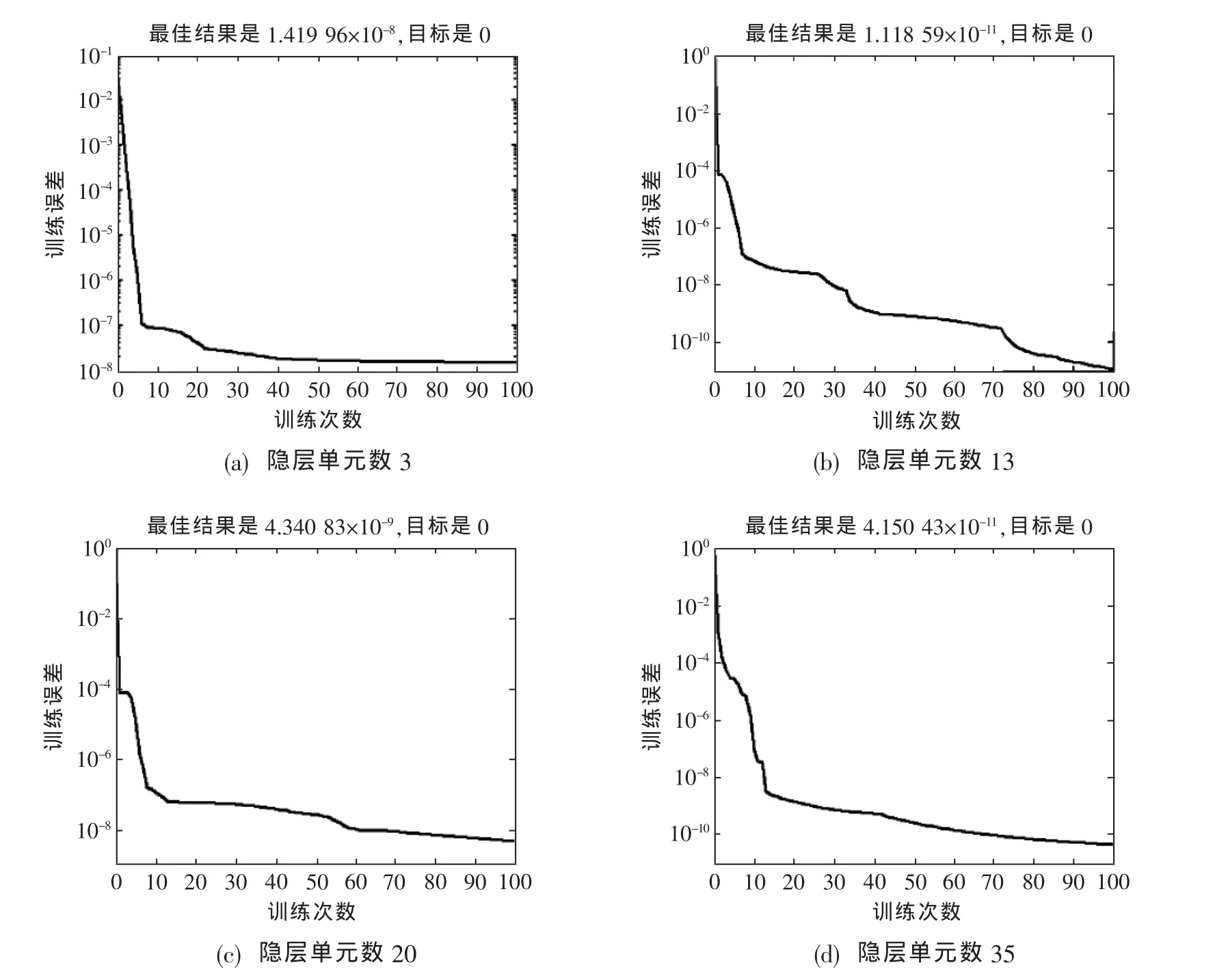
图2 BP网络训练误差曲线Fig.2 The curves of training error of BP network

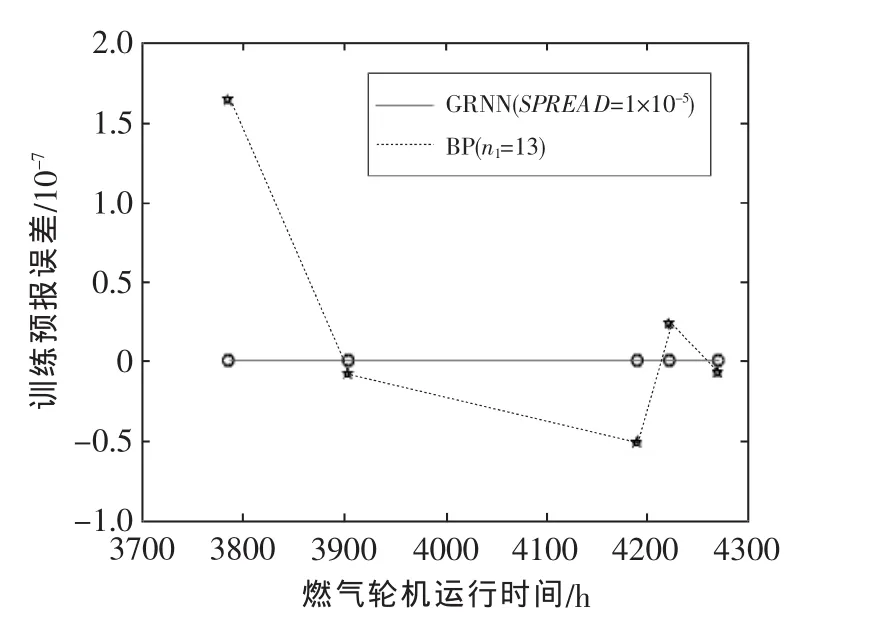
图3 BP网络(n1=13)和 GRNN网络(SPREAD=1×10-5)训练后的预报误差对比(样本16～20)Fig.3 Forecasting error contrast of BP(n1=13)and GRNN(SPREAD=1×10-5)after training(samples 16～20)

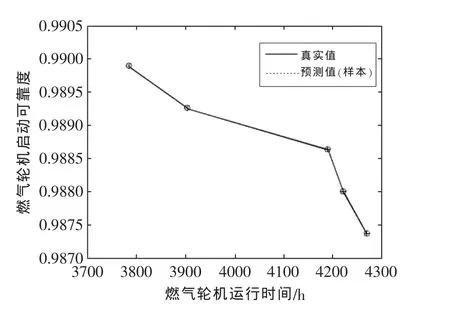
图4 GRNN网络预测值和真实值(样本16～20)Fig.4 The sample value vs.forecasting value of GRNN(samples 16～20)

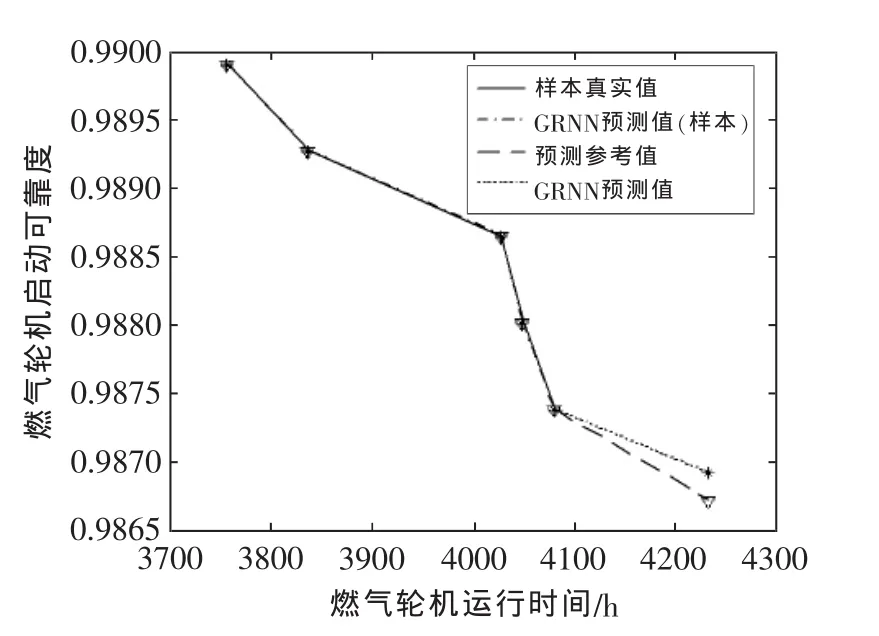
图5 基于GRNN网络的燃气轮机可靠性预测Fig.5 The reliability forecasting with GRNN

5 结论

(1)利用神经网络能够解决高度非线性问题，显示出其优良的逼近非线性函数的能力；而常规的回归方法却无能为力。所以神经网络为燃气轮机可靠性预测提供了一个有力的工具。

(2)无论是用BP网络还是GRNN网络，在算法实现中都需要采用恰当的参数才能得到较好的效果。BP网络所需的参数设计为隐单元数，GRNN网络所需的参数设计为其分布密度。

(3)本例中，当分布密度为1×10-5时，GRNN网络在算法实现中的训练用时比BP网络的要少，而精度也要比最佳的BP网络(隐层单元数为13)的高。

[1]王少萍.工程可靠性[M].北京：北京航空航天大学出版社，2000.

[2]Haykin S.神经网络原理[M].叶世伟，史忠植，译.第二版.北京：机械工业出版社，2004.

[3]吴晓平，汪 玉.舰船装备系统综合评估的理论与方法[M].北京：科学出版社，2007.

[4]朱大奇，史 慧.人工神经网络原理及应用[M].北京：科学出版社，2006.

[5]Moody J，Darken C.Fast Learning in Networks of Locally-tuned Processing Units[J].Neural Computation，1989，1(2)：281—294.

[6]Powell M J D.Radial Basis Function for Multivariable Interpolation[C]//.A review,IMA Conference on Algorithms for the Approximation of Functions and Data.England，1985.

[7]Broomhead D S，Lowe D.Multivariable Functional Interpolation and Adaptive Networks [J].Complex Systems，1988，2(2)：321—355.

[8]Poggio T，Girosi F.Regularization Algorithms for Learning that are Equivalent to Multilayer Networks[J].Science，1990，127：978—982.

[9]Sprecht D F.A General Regression Neural Network [J].IEEE Trans Neural Networks，1991，2(6)：568—576.

[10]周 昊，郑立刚，樊建人，等.广义回归神经网络在煤灰熔点预测中的应用[J].浙江大学学报(工学版)，2004，38(11)：1479—1482.

[11]鹿 鹏，陈晓平，赵长遂，等.高压密相气力输送固相流量的实验与GRNN网络预测[J].热能动力工程，2008，23(1)：41—45.

[12]董长虹.Matlab神经网络与应用[M].北京：国防工业出版社，2007.

[13]葛哲学，孙志强.神经网络理论与MATLABR2007实现[M].北京：电子工业出版社，2007.