某型发动机空气流量计算影响因素研究

王 红，马明明

(中国飞行试验研究院，陕西 西安 710089)

1 引言

发动机空气流量是发动机试验的一个重要参数，也是发动机性能参数推力和耗油率的重要计算依据[1，2]。本文通过采用不同方式计算某型发动机地面及空中特定状态空气流量，来研究进/发气动界面空气流量计算结果的影响因素和影响程度。

2 试验方案

2.1 测点布局

在进气道与发动机的气动界面上安装总静压测量耙及附面层总压测量耙，测取发动机进口总静压参数，如图1所示，总静压测量耙的6只耙沿周向均匀分布，每只耙上布置5个皮托管式受感部，可同时测量当地总压和静压。受感部按等环面分布，沿轴向高出耙体4 cm。为方便后续表述，定义耙号(从右水平耙开始沿顺时针依次为1号、2号、……、5号、6号)及转数(从靠近壁面的一转测点开始至中心的一转测点依次为第1转、第2转、……、第5转)。附面层总压测量耙为3只，等角度布置。总温测点位于截面正下方距壁面4 cm处。

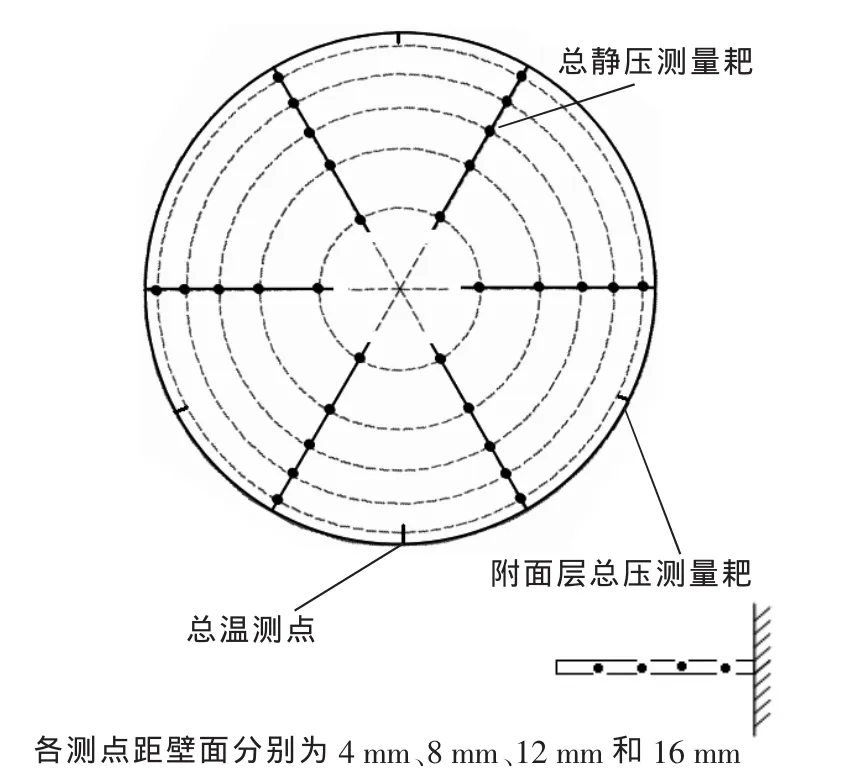
图1 总静压测点在气动界面上的分布Fig.1 Stations of total pressure and static pressure at AIP

试验前，对选用的压力传感器进行了校准，确保压力测试精度在0.5%以内；对受感部至传感器之间的管路进行了密封性检查，确保管路无堵塞、无漏气。

2.2 计算方式

本文采用三种方式计算空气流量：

方式一，利用总静压耙参数将界面分为5个环面(最里面的环面实际为圆面)，各环面的总静压值为该转总静压的环面积分均值，应用公式分别计算各环面的空气流量，计算结果累加即为整个截面空气流量。

方式二，利用总静压耙参数将界面分为5×6个扇形区域，各扇形区域的总静压为中心代表点的总静压值，应用公式分别计算各扇形区域的空气流量，计算结果累加即为整个界面空气流量。

方式三，在方式二的基础上，利用附面层总压耙参数计算靠近壁面的空气流量，附面层总压计算区域内的静压采用总静压耙第1转的静压值，即原第1转计算的空气流量由第1转与附面层总压参数共同计算的结果替代，各转计算结果累加即为整个截面空气流量。

3 试验结果

地面静止和空中飞行试验中若干条件下发动机特定状态空气流量的计算结果如表1所示。

同时，为了验证本文试验计算结果的合理性和准确性，采用CFD软件计算了空气流量。CFD计算区域网格划分和边界条件设定见图2，远场进口由大半球的球形表面组成，给定当地静压；出口由两部分组成，一是大半球中截圆面与吊舱表面所围成的环面，给定当地静压，二是进/发气动界面，按照试验值给定面平均静压。

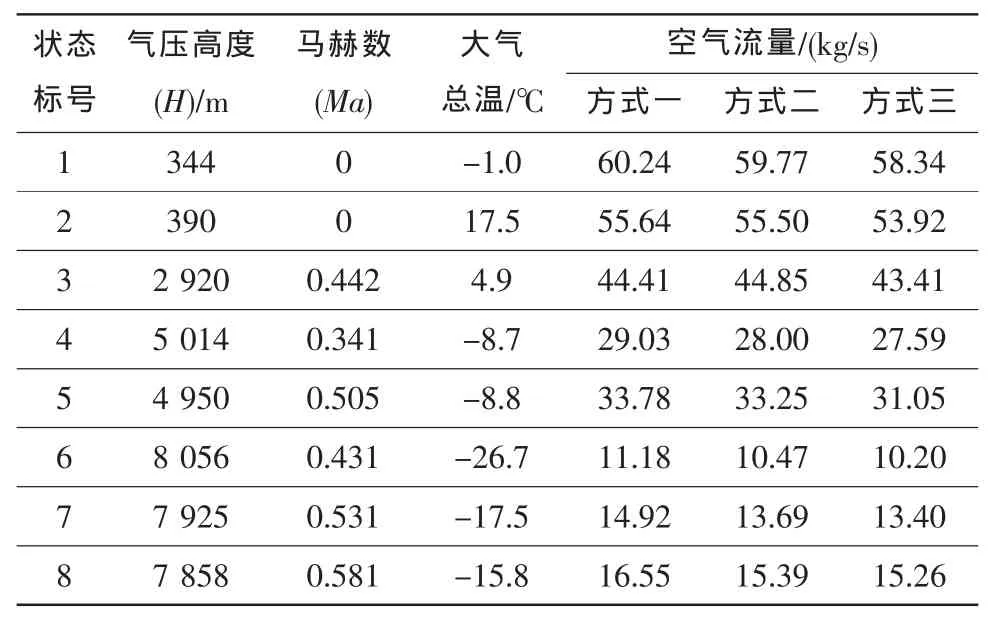
表1 采用三种方式计算的空气流量Table 1 Airflow calculation results with three different methods

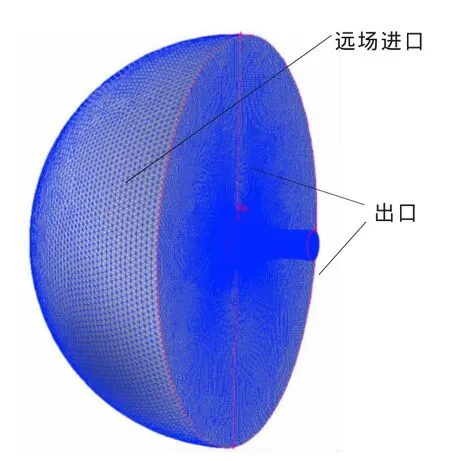
图2 CFD计算网格划分及边界标示Fig.2 Grid division and boundary identification of CFD calculation

图3 为H=344 m、Ma=0时CFD计算的气动界面总压分布，计算流量为60.50 kg/s。考虑到CFD计算中进气道出口只给定面平均静压而未考虑静压的不均匀性，因此这一结果与试验计算结果58.34～60.24 kg/s相比还是比较接近，这也验证了试验计算结果的合理性和准确性。

图3 CFD计算的气动界面总压分布(H=344 m，Ma=0)Fig.3 Total pressure contours at AIP calculated by CFD(H=344 m,Ma=0)

4 空气流量计算结果影响因素分析

4.1 内圈总静压径向不均匀性的影响

用于计算空气流量的测量耙在装机之前，一般要进行同规格测量耙试验件安装在筒体上的地面振动试验，以鉴定其在振动条件下的工作可靠性和结构完整性，振动等级要求较高。由于耙体一般采用悬臂式安装，筒体与耙体的共振频率往往会出现在发动机工作频率之内，加之没有相关的标准和依据，目前较为普遍的做法是缩短耙体长度，但这样做后，气动界面靠近中心区域的流量就不能准确测量。

本文采用的总静压测量耙为径向5点等环面设计。在此，假设缺乏第5转数据或第5转数据不可用，利用第4转数据代替对应耙上第5转数据(忽略内圈的总静压不均匀性)，研究内圈总静压径向不均匀性对空气流量计算结果的影响。

选取方式一的计算结果进行内圈总静压径向不均匀性对比，结果如表2所示。可见，对于该型发动机，是否考虑内圈总静压径向不均匀性的计算结果的绝对差值在0.7 kg/s以内，高度越低，空气流量值越大，绝对差值基本呈增大趋势；而相对差值随高度的降低呈减小趋势，地面试验计算结果相对差值在1.2%以内，气压高度小于5 000 m时可认为相对差值不大于1.6%，也就是说，此时如果缺乏第5转数据或第5转数据不可用，利用第4转代替第5转数据后，可参考以上相对差值对计算结果进行修正。

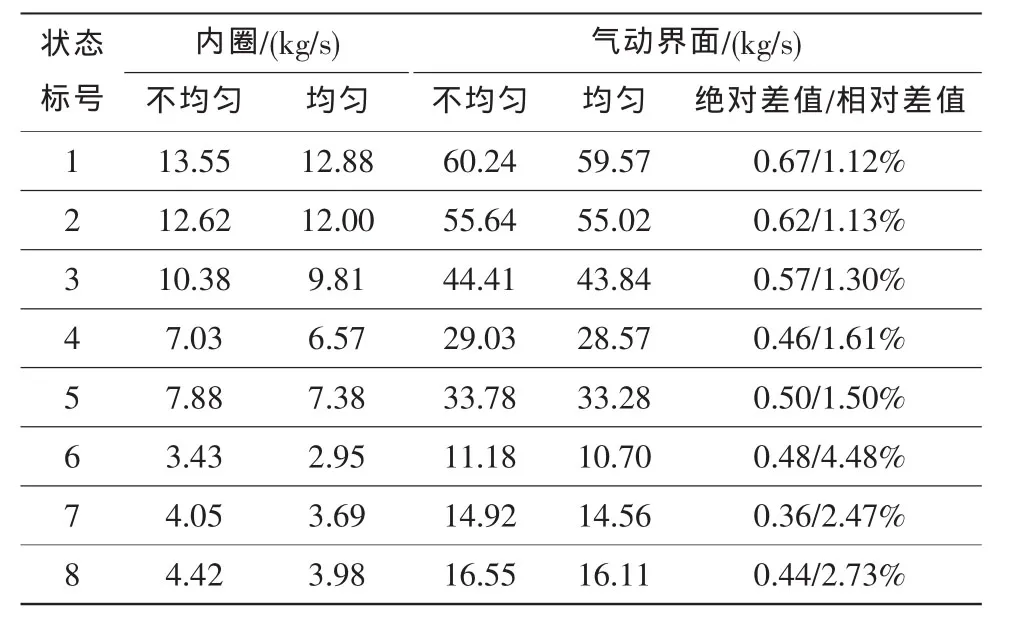
表2 内圈总静压径向不均匀性对空气流量计算结果的影响Table 2 The effect of radial ununiformity of inner total pressures and static pressures on airflow calculation results

4.2 总静压周向不均匀性的影响

方式一对环面总静压面平均后直接计算整个环面空气流量，即认为总静压沿周向均匀；方式二以当地总静压作为各扇形区域的总静压，计算各扇形区域后再进行累加，即考虑了环面内总静压的周向不均匀性。

由于本文不涉及侧风、攻角、侧滑角、进气道进口安装畸变发生器等，因此，进/发气动界面总静压周向不均匀性的影响因素只有空气自身重量和转子转向，而空气流量的周向不均匀性也由此导致。

图4中总静压分布并不沿竖直断面对称分布，而是基本呈与竖直断面形成一定夹角的断面对称分布，这是因为顺着航向看，发动机低压转子逆时针旋转，带动上游气流也沿逆时针偏转一定角度，这一点在CFD计算结果(不考虑其后转子运动)中模拟不到(见图3)。5号耙所在区域(对称断面上半部)总压较之面平均总压偏大约0.38%，静压较之面平均静压偏小约1.6%，从而导致5号耙所在区域流量密度较之面平均流量密度高出约1.4%，如图5所示。

图6为H=4 950 m、Ma=0.505时气动界面的总静压分布，可见，如上所述，气动界面的高总压、低静压分布区域在空中飞行条件下亦是如此。

从表3中的总静压周向不均匀性对空气流量计算结果的影响可以看出：地面静止条件下，方式一与方式二的计算结果的绝对差值和相对差值都较小，说明地面试验总静压周向分布较均匀；空中飞行条件下，方式一与方式二的计算结果差异较大，说明空中飞行条件下总静压周向很不均匀。方式二与方式一的结果相比，有大有小，大时说明局部扇形区域静压与总压比值小，而沿周向面平均后增大了该比值，因此方式一降低了该区域的空气流量，反之则增加了该扇形区域的空气流量。

4.3 最外转静压作为气动界面平均静压的影响

空气流量测量耙的设计也采取过 “总压耙+壁面静压孔”的方式，即仍采取多耙多点方式测取整个气动界面当地的总压，而认为气动界面的静压均匀一致，只在壁面打孔布置若干测点测取壁面静压作为整个气动界面的静压值。

在此，讨论以最外转静压作为气动界面平均静压对空气流量计算结果的影响。选取部分飞行状态，采用方式二与用最外转静压作为气动界面平均静压计算的空气流量结果对比如表4所示。可见，如果用靠近壁面的静压替代当地静压，将使计算结果与实际空气流量相差10%以上。本文用总静压耙上最外转静压替代界面平均静压，实际上壁面静压比总静压耙上最外转静压更大，带来的计算结果差值也更大，原因是界面静压分布很不均匀，也就是说，用“总

压耙+壁面静压孔”获得的数据进行流量计算不准确，需要进行修正，表4的相对差值可作为修正参考。

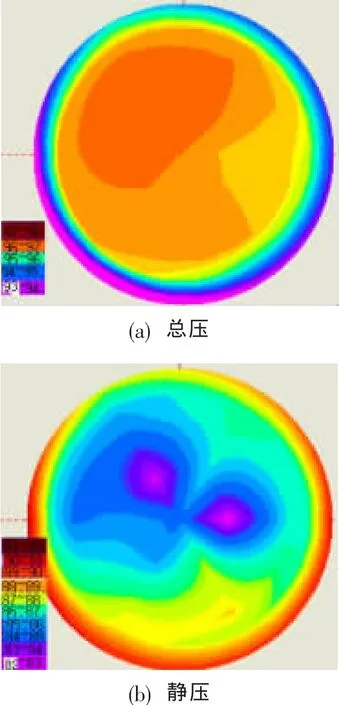
图4 气动界面总静压分布(H=390 m，Ma=0)(顺航向)Fig.4 Total pressure and static pressure contours at AIP(H=390 m,Ma=0)

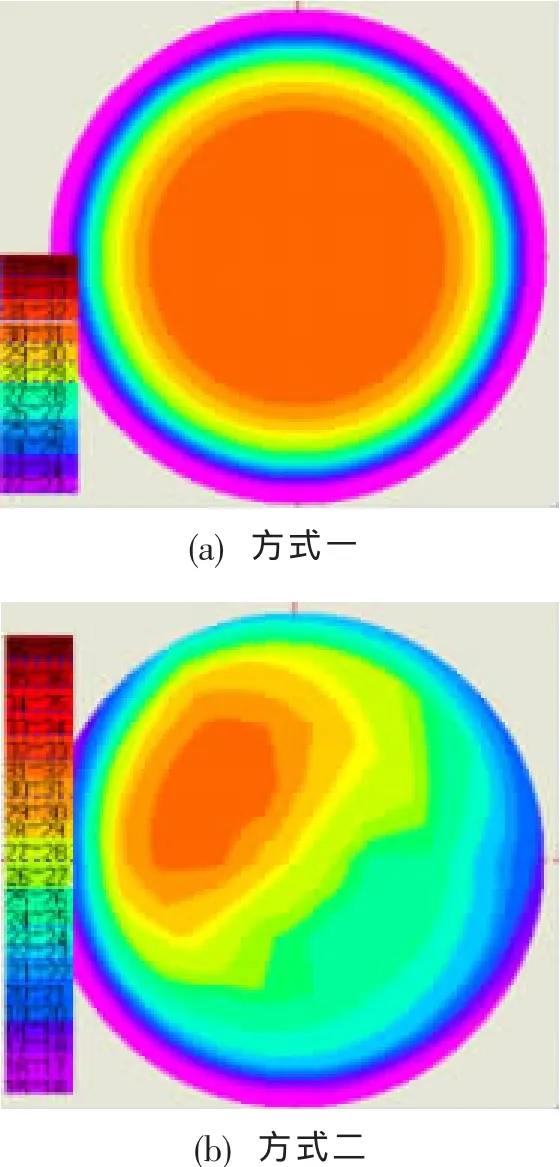
图5 方式一和方式二计算的流量分布(H=390 m，Ma=0)Fig.5 Airflow contours at AIP calculated with two different methods(H=390 m,Ma=0)

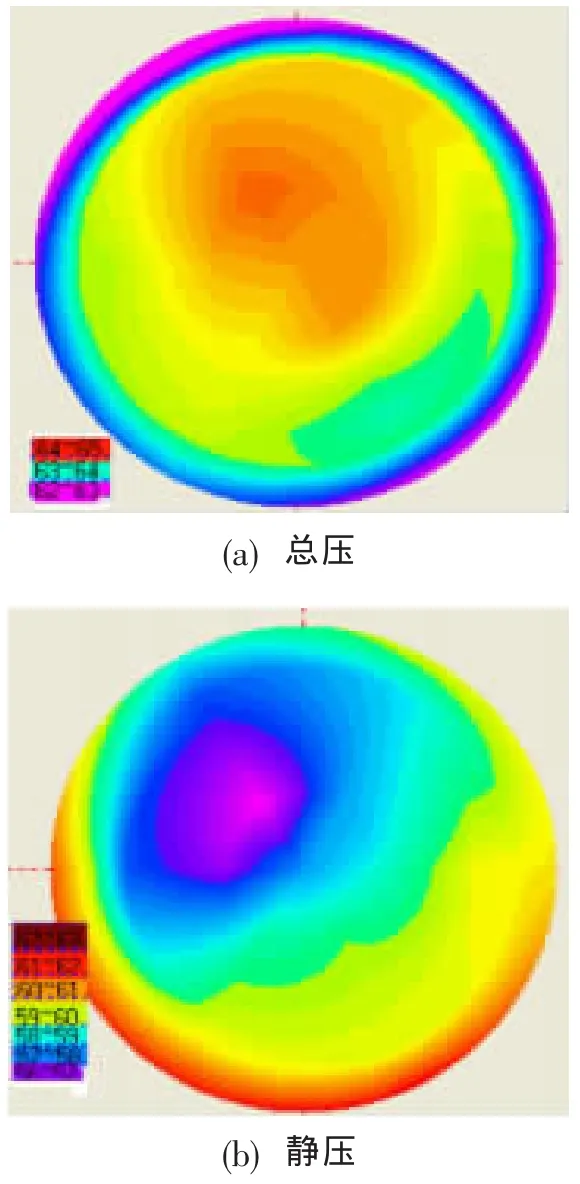
图6 气动界面总静压分布(H=4 950 m，Ma=0.505)Fig.6 Total pressure and static pressure contours at AIP(H=4 950 m,Ma=0.505)

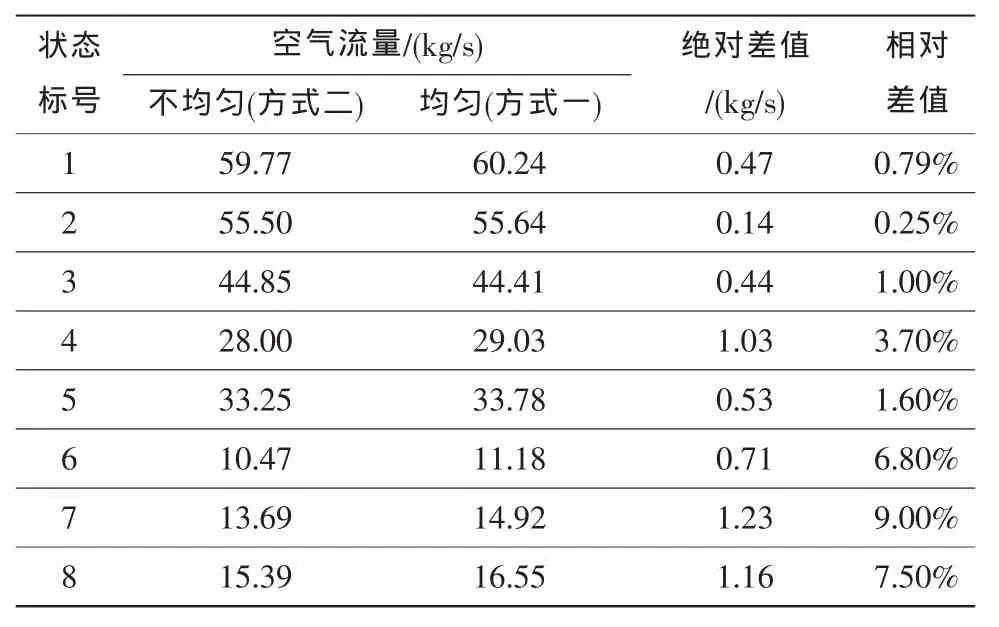
表3 总静压周向不均匀性对空气流量计算结果的影响Table 3 The effect of circumferential ununiformity of total pressures and static pressures on airflow calculation

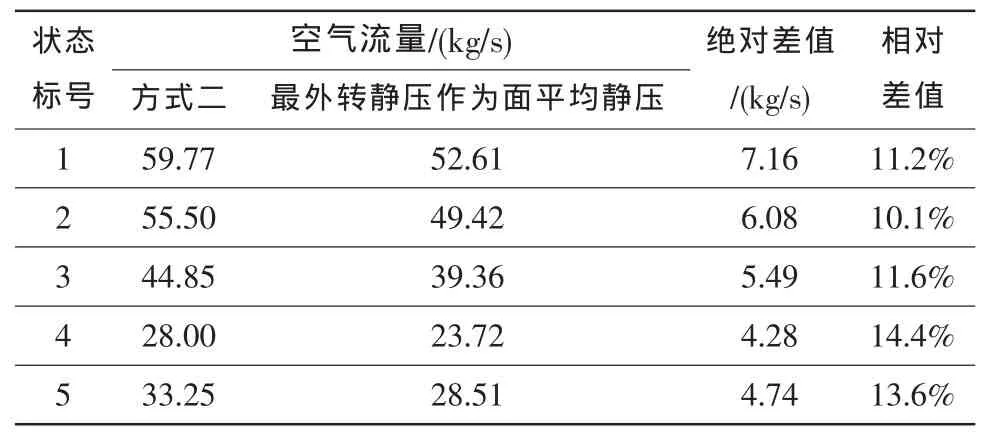
表4 最外转静压作为面平均静压时的空气流量计算结果Table 4 Airflow calculation results using outer static pressures as average static pressure at AIP

4.4 近壁面流动的影响

由于壁面的粘滞阻力，近壁面流体压力梯度很大，存在附面层。本文在方式二的基础上，利用附面层总压耙参数修正最外圈的空气流量，即将原只利用总静压测量耙第1转总静压参数计算最外圈空气流量的方式二，改变为同时结合附面层总压耙参数计算的方式三。

从表5可以看出，两种计算方式的绝对差值和相对差值虽没有明显的变化规律，但不考虑近壁面流动影响计算的空气流量比实际值大一些，最大可能会大3%～4%。特别是地面试验，相比于最内圈总静压不同方式取值带来1.2%以内差值以及总静压沿周向不均匀性带来0.8%以内差值，是否考虑近壁面流动带来的流量差值显得很大。

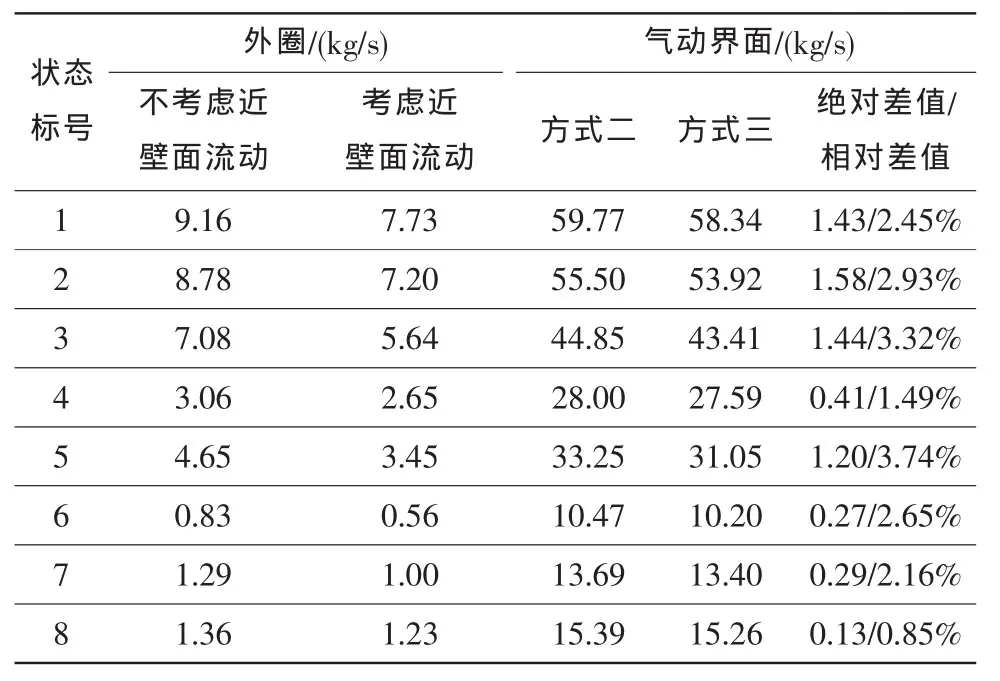
表5 是否考虑近壁面流动时的空气流量计算结果Table 5 Airflow calculation results based on boundary layer

5 结论

(1)发动机进口总静压图谱的对称面取决于其后转子的转向，转子逆时针旋转，对称面相对竖直断面逆时针旋转一定角度，反之亦然。对称面上半部所在区域的总压较之其它区域偏大，静压偏小，空气流量偏大，但总静压的周向不均匀性对整个界面的空气流量影响不大。

(2)如果缺乏第5转数据或第5转数据不可用，利用第4转数据代替第5转数据，地面试验计算结果相对差值在1.2%以内，而气压高度小于5 000 m时可认为相对差值不大于1.6%。

(3)采用“总压耙+壁面静压孔”获得的数据计算的空气流量与实际值相差10%以上。

(4)不考虑近壁面流动影响计算的空气流量比实际值大一些，最大可能会大3%～4%。

(5)结合结论(2)～(4)，在条件允许的情况下，应尽可能采用“总静压一体耙+附面层总压耙”或“总静压附面层一体耙”进行测量。

[1]杜鹤龄.航空发动机高空模拟[M].北京：国防工业出版社，2002.

[2]徐 国，郭 昕，陈建民.高空台标定中空气流量测量方法研究[J].燃气涡轮试验与研究，1995，8(2)：40—43.