基于PEM的辅助动力装置系统辨识与仿真

江 群，王道波，李 猛

(南京航空航天大学 自动化学院，江苏 南京210016)

1 引言

辅助动力装置(APU)是加装一套或几套独立于主发动机的动力系统，是一种能输出增压气源和轴功率的小型发动机[1]。其主要作用是用来起动主发动机，驱动发电机和液压泵为飞机提供备份电源及液压源，同时还可以向座舱空调系统提供气源。辅助动力装置与普通发动机有很大的不同，其启动过程异常复杂，难度很大，目前国内尚无起动过程的准确模型。另外，APU的工作特性决定了要求其快速到达额定状态，且在功率提取时保证转速在小范围变化，即要求其绝大多数工作状态在等速状态。为了研究APU的性能和控制规律，必须建立APU的模型。发动机模型主要分为部件级模型和“小偏差”模型[2]：其中部件级模型主要是通过部件特性建立其数学模型，虽然精确但要详细了解部件特性且不具备实时性；“小偏差”数学模型不需要了解其详细的部件特性，根据工程试验数据就可以建立实时简化的数学模型，该简化模型能模拟APU稳态、动态及起动过程。本文根据某型APU的试验数据，采用预测误差法(PEM)来建立其动态模型。这种方法的基本思想与最小二乘法的完全不同，它只需要确定一个预报误差准则函数，并利用预报误差信息来确定模型参数。相对于极大似然参数估计法，PEM具有的优点是不要求已知数据的概率分布式，所以其使用范围更加广泛[3]。本文在介绍涡轮动力装置的工作原理基础上，提出了电子仿真试验器的设计原理和实现方法，最后将该试验器用于某型涡轮动力装置的闭环控制并对其仿真结果进行分析。

2 系统辨识原理及预测误差法

所谓系统辨识，就是通过研究对象的输入信号作用下的输出响应，对输入、输出数据进行处理和计算，估计出对象的数学模型[4]。辨识由数据、模型和准则这三个要素组成，利用数据，通过准则优化在模型类中找出最佳模型。系统辨识的内容包括四个方面：①辨识目的；②模型结构辨识；③模型参数辨识；④验证模型。本文采用PEM对模型参数进行辨识。

描述动态系统的模型的一般形式为：

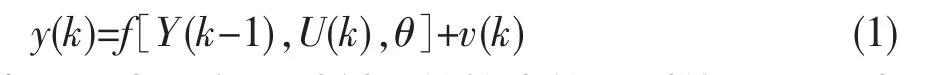
式中：y(k)表示在k时刻系统输出的观测值；Y(k-1)表示k-1时刻以及之前的输出观测数据的集合表示k时刻以及之前的控制变量的集合为系统的参数向量；v(k)是具有零均值和均方差阵Σ的信息序列。

采用PEM估计参数θ，可以根据给定的数据构造如式(2)的预测误差模型：

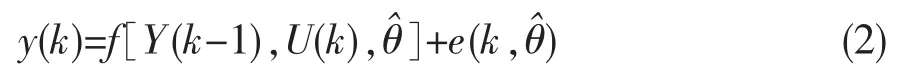
根据参数估计的PEM的原理，采用式(3)或式(4)作为极小预测误差准则来获得系统输出y(k)的最优预报。

采用以上方法对模型参数进行辨识，首先要选择合理的采集数据，并对数据进行跳点剔除、平滑处理；其次是选择合适的模型阶数，利用PEM进行模型参数辨识；最后对所辨识的模型进行仿真验证。

3 模型参数辨识及仿真结果分析

本文研究的对象某型辅助动力装置，虽然是一个复杂的非线性系统，但是其尾喷管不可调，是非加力、单轴小型发动机，而且如果发动机处在“小偏离”状态，即输入量在很小的范围内变化，则发动机的工作状态在某一稳态附近，在该稳态点对发动机的非线性方程进行Taylor公式展开，忽略高次项的影响，这时发动机模型可表示为线性时不变模型。研究该型APU的“小偏离”模型，主要是以APU的转速N(%)作为被控量，选择供燃油量wf作为控制量。在地面台架试车试验中，采集燃油流量作为输入量，转速百分比作为输出。试验过程中，采集时间间隔为0.25s。

3.1 数据预处理

由于发动机导叶角以及尾喷管面积不可调，理论上来说，稳态时各状态参数如涡轮转速、空气流量等都与燃油流量一一对应。但在实际试验过程中，受试验发动机、试验环境和设备等诸多因素的影响，试验所得稳态数据经换算后存在明显的偏离总体变化趋势的个别突变稳态点(即跳点)。如果对这些跳点不加以去除，势必会影响辨识的结果。本文采取简单的低阶多项式滑动拟合法来判断和剔除跳点[5]，某燃油流量跳点剔除前后的数据对比如图1所示。比较图1中的曲线可以发现，低阶多项式滑动拟合法能有效去除采集过程中的跳点，使数据可靠性变高。

通常情况下，在跳点剔除处理后，试验数据仍然存在着各种误差及较强的噪声干扰。为保持合理的信噪比，还需对采集的输入、输出数据进行平滑处理，以消除实测数据中各种噪声和系统误差，提高辨识精度。本文主要利用MATLAB系统辨识工具箱中idfilt函数的Butterworth滤波器对数据进行滤波，去除噪声分量，再利用idresamo函数对输入、输出数据进行重新采样来插值或删减数据[5，6]。经上述方法平滑处理前后的部分曲线如图2、图3所示。从图中可以看出，原来试验采样时间为0.25 s，误差较大，经处理后，数据明显平滑。本节只给出某种条件下的数据预处理效果图，对于其它环境条件下的数据，可采用相同方法进行处理。

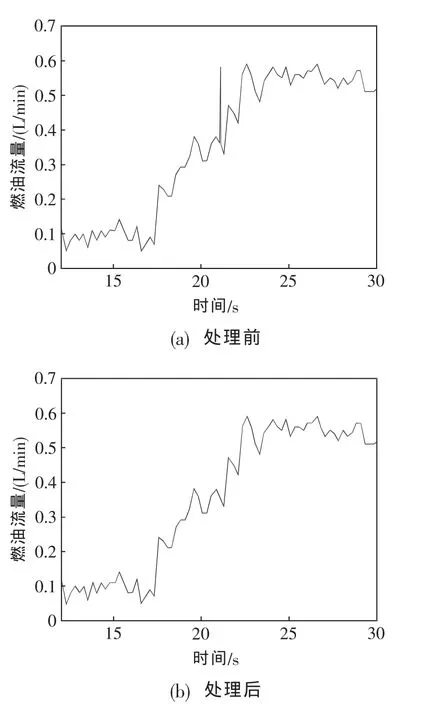
图1 燃油流量跳点处理前后比较曲线Fig.1 Before and after processing curves of sudden change points in the fuel flow

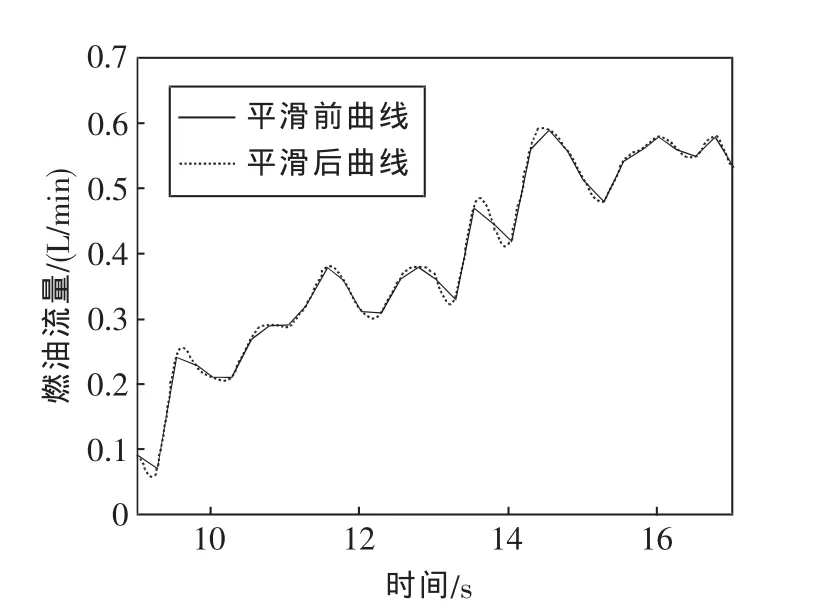
图2 燃油流量平滑处理曲线比较Fig.2 Comparison of fuel flow smoothing curves

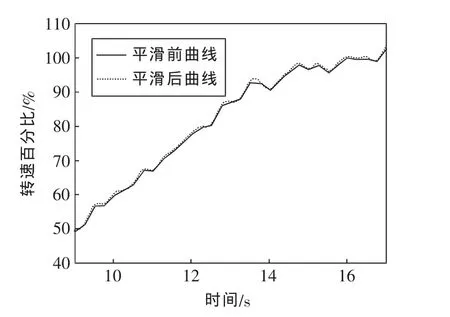
图3 转速百分比平滑处理曲线比较Fig.3 Comparison of speed percentage smoothing curves

3.2 模型结构和模型参数辨识

采集数据预处理后进行参数辨识，在辨识参数之前应确定模型的阶数。由于某型辅助动力装置为非加力且尾喷管不可调，因而在某一稳态点附近可简化为线性时不变系统。采用一阶系统满足不了精度的要求，而采用三阶系统会使整个系统变得复杂。仿真结果表明，二阶系统足以满足APU的精度要求，所以模型阶次选为二阶，设定待辨识参数为θ=本文选用该型APU以进入闭环控制阶段的85%～96%额定转速段所测数据进行数学模型辨识，运用上述方法辨识所得的参数估计值为：a1=-1.486，a2=0.506 2，b1=29.42，b2=-9.496。

系统的传递函数为：

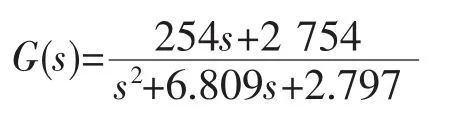
辨识所得曲线如图4所示，拟合度为96.06%。从上述辨识结果可见，采用该方法拟合的效果很好，能满足辅助源动力装置转速的动态特性。对于辅助动力装置其它不同阶段的数学模型，可采用相同方法对采集的数据进行辨识分析，得到各个数据段的模型参数。

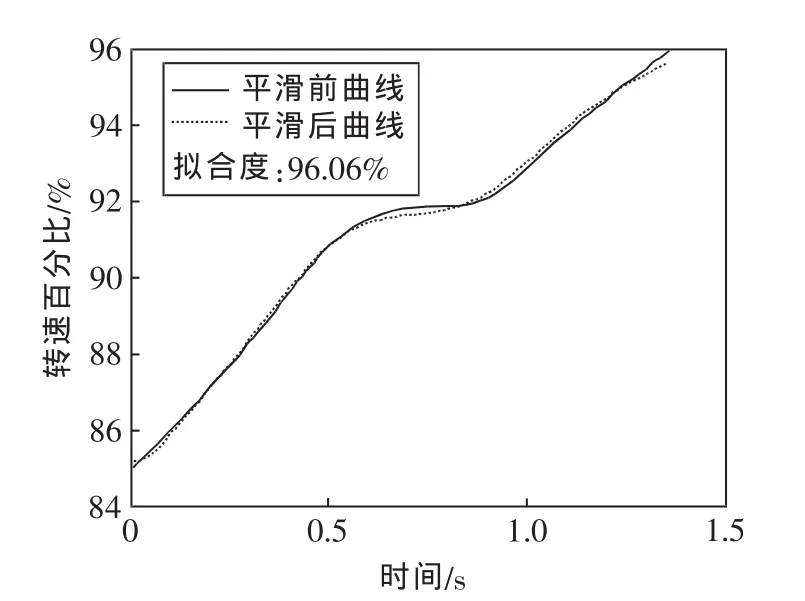
图4 二阶模型辨识结果Fig.4 Identification result curves of second-order model

3.3 验证模型

模型参数辨识后，还需要对所辨识模型的通用性和正确性进行验证。本文选用另一组燃油流量输入数据验证模型。将试验数据的输入量作为辨识模型的输入量，经模型计算，得到模型输出量；再将模型输出量与试验输出量进行比较。其模型验证曲线如图5所示，可以看出，模型输出数据与试验数据吻合度很高，达到了模型建立的精度要求，可以将该模型用于以后的仿真研究。

图5 模型验证曲线Fig.5 Model validation curves

4 结束语

本文通过预测误差法辨识某型辅助动力装置的简化模型，大大减少了计算量，简化了建模过程。仿真结果表明，所建模型的输入和输出与实际试验结果吻合度很高，本文所用辨识方法是可靠、有效的，因而可以以该模型为基础对某型辅助动力装置的控制系统进行设计。不过本文辨识的辅助动力装置的数学模型是根据地面台架试车数据辨识的，因此本文辨识的数学模型仅能描述地面工作状况，为了使模型能适应大偏差的工作范围，还需要在各种工作负载和飞行高度下进行辨识验证。

[1]钱小娟.某型APU控制系统的设计与台架试车[J].航空兵器，2008，(3)：42—44.

[2]赵 琳，樊 丁，陕薇薇.单轴航空涡扇发动机数学模型辨识[J].推进技术，2008，29(6)：733—736.

[3]方崇智，萧德云.过程辨识[M].北京：清华大学出版社，1988.

[4]刁启娜，王 曦.系统辨识在航空发动机中的应用[C]//.中国航空学会第十一届发动机自动控制学术讨论会议.2002.

[5]刘叔军，盖小华，樊 军，等.Matlab7.0控制系统应用与实例[M].北京：机械工业出版社，2006.

[6]Ljung L J.Matlab System Identification Toolbox User’s Guide[M].The MathWork,Inc.，2003.