水滴撞击特性的重力影响分析

闵现花，董 葳，朱剑鋆

(上海交通大学 机械与动力工程学院，上海200240)

1 引言

飞机在含有过冷水微滴的云层中飞行时，机身部件如风挡玻璃、机翼和垂尾等，可能会出现结冰现象。机翼前缘结冰后，会引起最大升力系数降低，失速攻角提前，并使飞机的阻力增加，升阻比下降[1]；尾翼结冰除影响飞机的空气动力性能外，还影响航向的保持，特别是水平尾翼积冰着陆时，会产生下俯力矩，导致机头下俯[2]。而发动机进气系统导向叶片结冰，可能会导致冰脱落时进入发动机内部，损坏发动机，造成事故。另外，航空发动机导向叶片由于几何尺寸和流通面积都比较小，即使少量的结冰都足以引起发动机性能急剧下降。

为了保证飞行安全，必须对飞机进行一系列的防冰实验和相关数值模拟研究。美国联邦航空条例FAR25部附录C中规定，影响飞行安全的水滴平均有效直径在10～40 μm之间，这一数据在过去几十年里一直应用于防冰实验和数值模拟[3]。而在实际飞行气象条件中，飞机会遇到直径远大于40 μm的过冷水滴。1994年ATR-27飞机的飞行事故，使人们认识到低空的过冷大水滴(SLD)会导致更为严重的结冰[4]。由于其直径较大，运动过程中受重力的影响非常明显，相对于FAR25中规定的平均有效直径为10～40 μm的水滴，其运动轨迹、水收集区域和水收集量都发生了很大的变化。目前，国外对SLD已经开展了很多研究[3，4]，而国内的研究则相对较少。本文以NACA0012翼型为研究对象，分析了重力对水滴撞击特性的影响，获得了SLD的撞击特性。

2 水滴运动方程的确定

目前，对于水滴运动轨迹与撞击特性的计算主要有欧拉法和拉格朗日法两种方法。欧拉法是将过冷水滴和空气看作均相的两相流，在欧拉坐标系下建立水滴运动方程，水滴撞击特性和流场一起耦合计算，同时获得水滴撞击特性和流场计算结果；拉格朗日法是在获得部件周围流场分布的前提下，根据牛顿第二定律建立单个水滴的运动方程，求解该运动方程即可得到水滴的运动轨迹。由于空气中过冷水滴含量较少，并且其体积很小，因此可以忽略水滴对流场分布的影响，将水滴运动方程求解和流场计算分开进行，从而使得求解过程大大简化，因此拉格朗日法被广泛应用于结冰研究[5]。

本文采用拉格朗日法建立过冷水滴的运动方程，并作如下假设：①过冷水滴在流场中均匀分布，且以球形存在，不分解，不变形；②水滴在运动过程中其温度、粘性、密度等介质参数保持不变；③由于水滴密度远大于空气密度，由压力梯度而引起的力和表观质量力都很小，可忽略不计，同时还可忽略气动升力，因此只考虑作用在水滴上的粘性阻力和重力。

由牛顿第二定律，水滴运动方程可写成[6，7]：

式中：mw为水滴质量，且为水滴半径为重力加速度；为水滴在空气中所受的粘性阻力。可由下式确定：

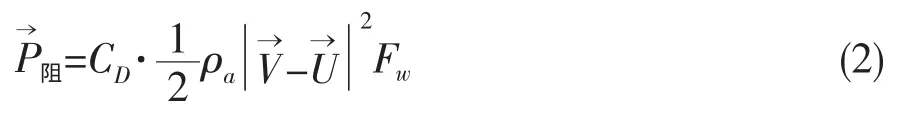
式中：CD为阻力系数；ρa为空气密度；V、U 分别为空气和水滴的运动速度；Fw为水滴迎风面积，且

将式(2)带入式(1)整理后得：

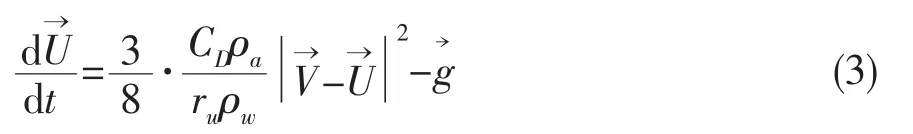
由于水滴沿水平方向运动，因此重力对水滴x方向的运动没有影响。将式(3)右端第一项分子分母同乘2rw/μa，经整理可得如下方程：

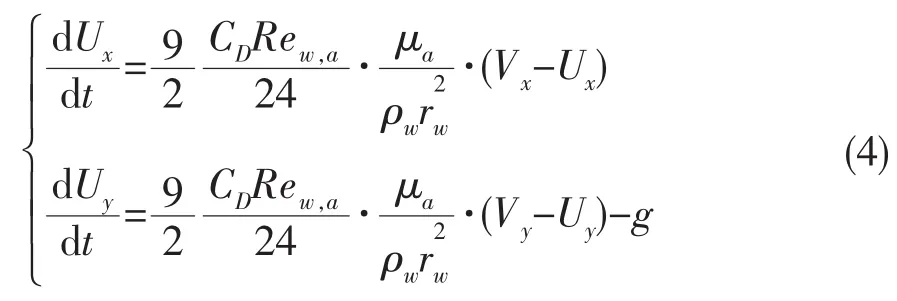
式中：μa为空气的动力粘度；下标x和y分别表示气流及水滴在x、y方向的分速度；Rew，a为水滴与空气的相对雷诺数，可由下式确定。

将水滴运动微分方程(4)转化成差分格式：

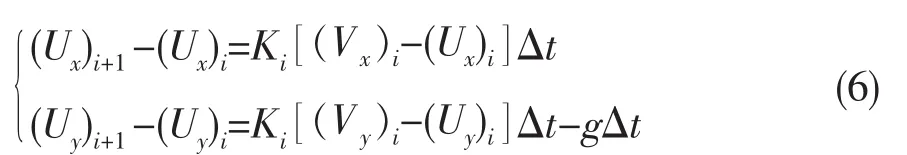
式中：下标i表示第i时刻，参数Ki可由下式确定。

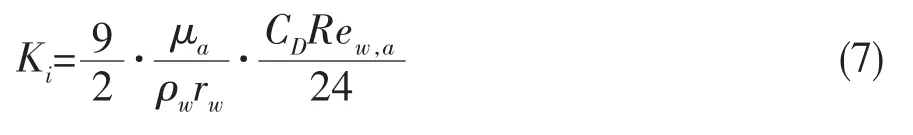
式(7)中的组合参数可由下式计算[6]：

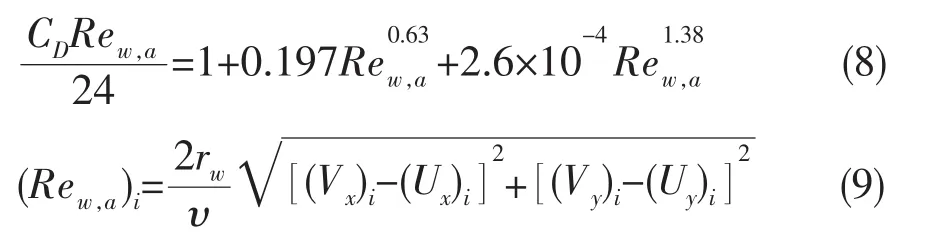
由式(6)得到水滴的轨迹方程为：

根据以上公式，通过Fortran编程，可求得水滴的运动轨迹、局部水收集系数和总收集系数等参数。

3 结果分析

本文中的算例共有6个，水滴直径分别为20 μm、40 μm、50 μm、70 μm、80 μm 和 800 μm。采用标准的NACA0012翼型进行计算，翼型厚度为0.12 m，弦长为1.00 m，攻角为0°，来流速度为 44.7 m/s，来流压力为94 500 Pa，来流温度为265.4 K。采用CFD软件FLUENT计算防冰表面的流场分布。图1为流场计算时采用的三角形网格。

以下各图中，C指翼型的弦长，S指落到翼型壁面的水滴点距离最前缘点的弧长，d指水滴直径，β指局部水收集系数，Em指总水收集系数。

3.1 重力对水滴轨迹的影响

图2给出了起始位置相同、水滴直径不同的轨迹图，并将考虑与不考虑重力的轨迹进行了对比。为了便于观察水滴落到壁面的终点位置，图中将翼型前缘壁面在y方向进行了放大。从图中可以看出，直径为20 μm时，考虑与不考虑重力时水滴轨迹基本重合；而当直径为50 μm时，水滴轨迹受重力的影响非常明显，终点位置偏差为2.3%(本文将偏差定义为两比较对象在y方向差值的绝对值与翼型厚度的比值)；当直径为80 μm时，终点位置偏差达4.9%；而直径为800 μm时，偏差已达8.2%。由此可见，随着水滴直径的增加，重力对水滴轨迹的影响越来越明显。

图1 翼型网格Fig.1 Grid distribution of the airlfoil

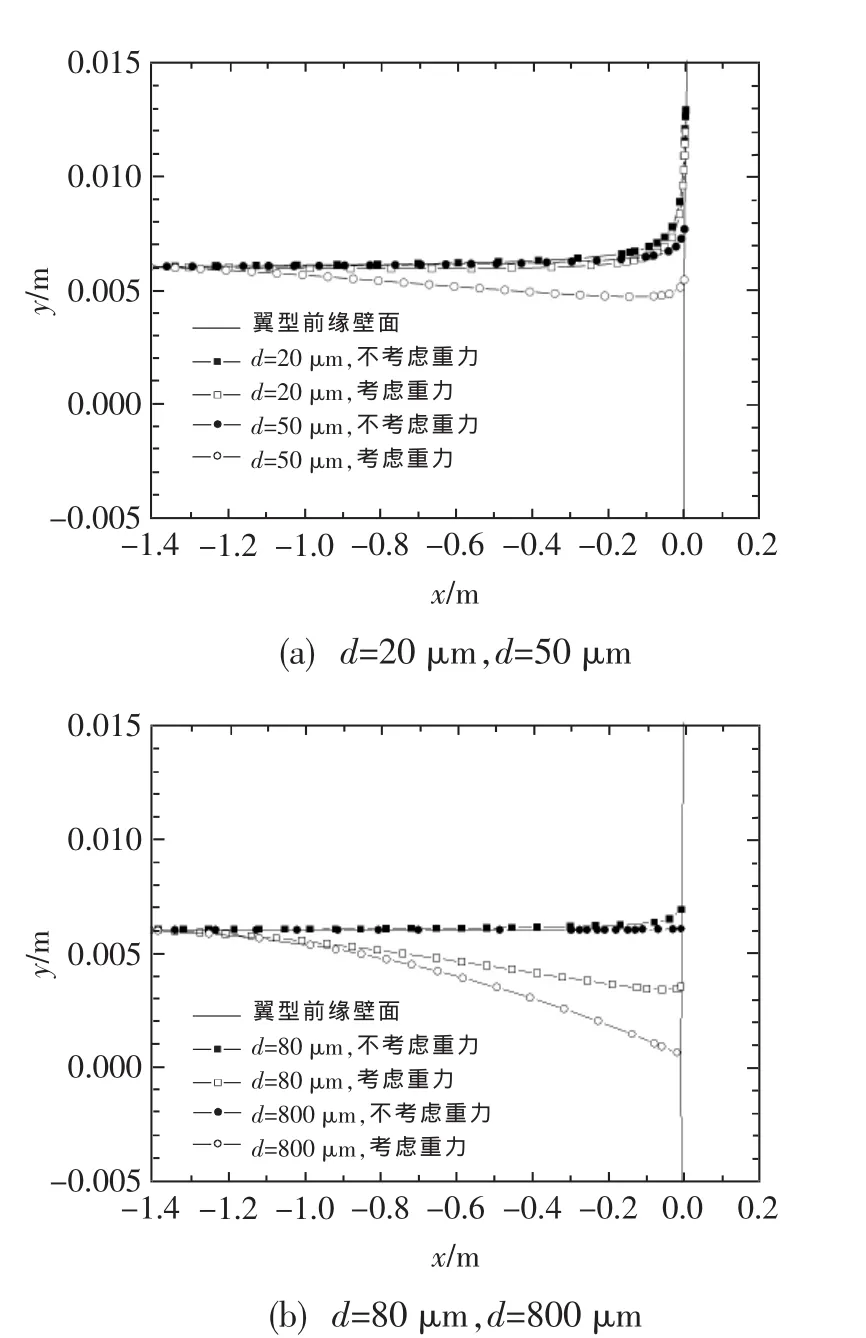
图2 水滴轨迹Fig.2 Droplet trajectory

3.2 重力对极限轨迹起始位置的影响

与机翼上、下表面相切的两条轨迹被称为极限轨迹，两条相切轨迹所包围的机翼表面即为水收集区域。图3给出了不同直径水滴在考虑与不考虑重力时的极限轨迹。由图中看出，当水滴直径为20 μm时，考虑与不考虑重力时上下两条极限轨迹的起始位置基本重合；而当直径为40 μm时，偏差开始比较明显；当水滴直径为50 μm和70 μm时，起始位置的偏差分别达到了3.3%和4.8%；当水滴直径为80 μm和800 μm时，由于受重力的影响，水滴极限轨迹的初始位置相对于不考虑重力的情况，分别向上偏移了5.0%和16.7%的距离。由此可知，随着水滴直径的增大，重力对两条极限轨迹起始位置的影响越来越明显，极限轨迹向上的偏移量越来越大。

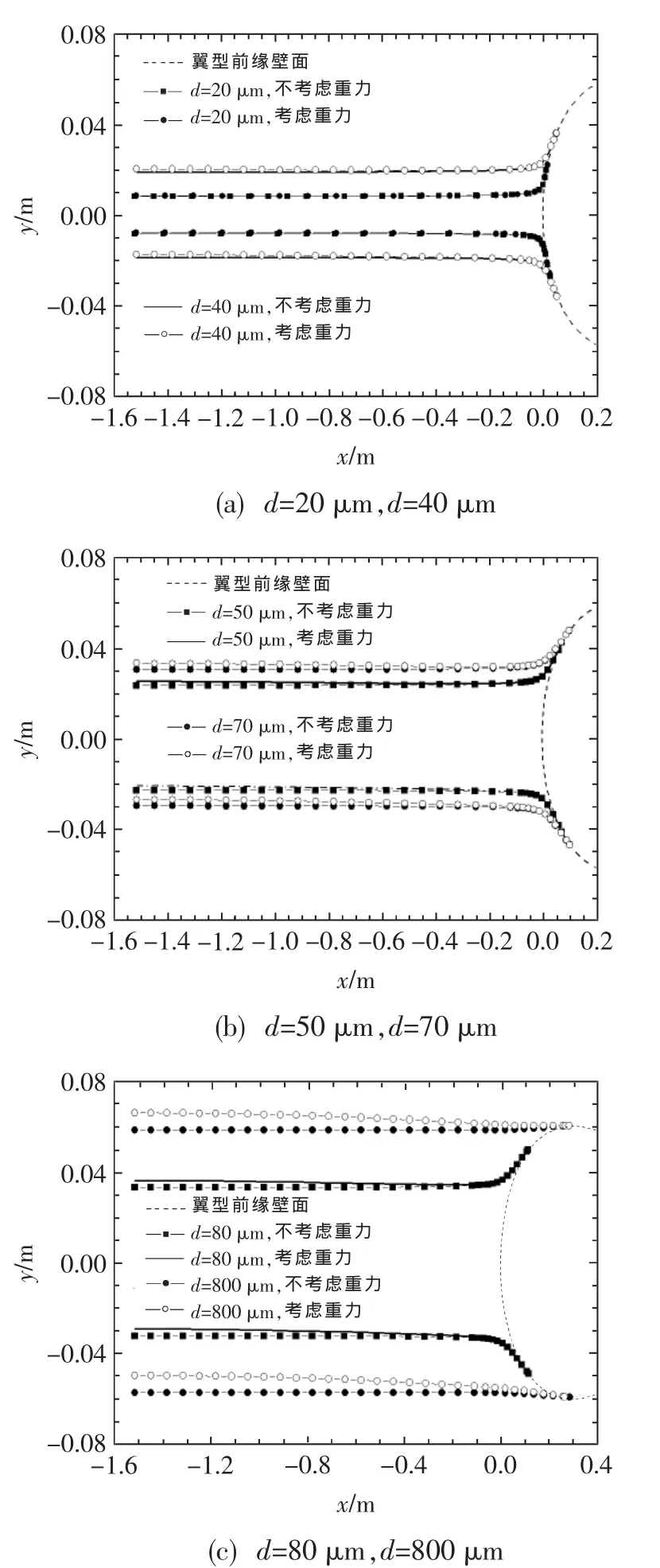
图3 水滴极限轨迹Fig.3 Droplet limiting trajectory

3.3 重力对水收集区域和局部水收集系数的影响

由图3中还可以看出，在相同直径条件下，考虑重力时水滴极限轨迹的终点位置与不考虑重力时的相同。因此重力对水滴收集区域的影响可以忽略。

图4给出了水滴直径为80 μm和800 μm时考虑与不考虑重力时的局部水收集系数。当水滴直径为80 μm时，考虑与不考虑重力时的局部水收集系数基本相同；当水滴直径为800 μm时，考虑重力时的局部水收集系数曲线向左略有偏移，表明水滴极限轨迹的终点位置往下略有偏移。因此可以认为，当水滴直径在800 μm以下时，重力对局部水收集系数的影响很小，可忽略；但当水滴直径大于800 μm或者水滴的起始位置距离机翼表面比较远时，重力对局部水收集系数的影响会变大，此时不能忽略。

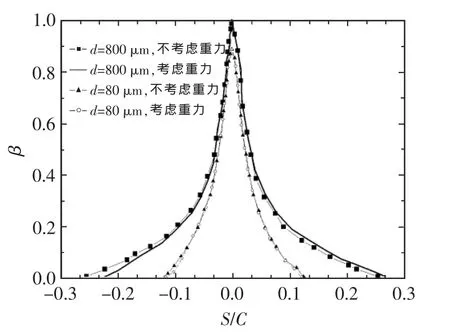
图4 局部水收集系数(d=80 μm，d=800 μm)Fig.4 Local collection efficiency(d=80 μm,d=800 μm)

4 实际应用

图5 给出了直径分别为 20 μm、40 μm、50 μm、70 μm、80 μm 和 800 μm 水滴的局部水收集系数。同时，计算得到以上各直径水滴的总水收集系数分别为：0.13、0.31、0.39、0.50、0.55 和 0.96。

由图5可以看出，随着水滴直径的增加，局部水收集系数不断增大。相对于直径为20 μm和40 μm的水滴，直径为50 μm的水滴不仅收集区域增大，而且在不同的收集位置其局部水收集系数都有较大的提高，由计算可知，其总水收集系数较直径为40 μm时增大了 25.8%，较直径为20 μm时增大了200%；当水滴直径为800 μm时，局部水收集系数接近于1.00，总收集系数达0.96，即机翼的迎风面几乎全部为结冰区。因此当水滴为SLD时，其水收集系数以及水收集区域都较FAR25中规定的10～40 μm的水滴有很大幅度的增加。

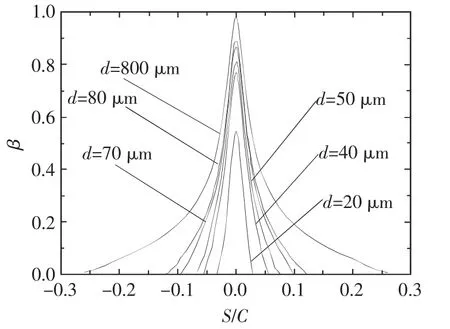
图5 不同直径水滴的局部水收集系数Fig.5 Local collection efficiency with different droplet diameters

由3.1和3.2的讨论可知，当水滴直径超过50 μm时，水滴轨迹和极限轨迹起始位置受重力的影响很大，此时不能忽略重力的作用。当水滴直径为800 μm时，由于受重力的影响，水滴极限轨迹的初始位置相对于不考虑重力的情况向上偏移了16.7%的距离(见图3)。因此，在冰风洞(如图6所示)试验中，当实验水滴为SLD时，靠近下方位置的水雾化喷嘴喷出的大水滴由于受到重力的影响，未到达实验部件就落到地面，而最上方喷嘴喷出的水滴则没有落到试验件上方的极限位置处。因此，可以适当减少下方喷嘴的数量，而相应增加上方喷嘴的数量。

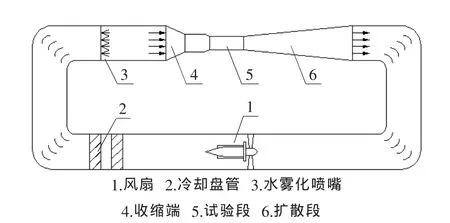
图6 冰风洞示意图Fig.6 Diagram of icing wind tunnel

5 结论

(1)水滴轨迹受重力的影响随直径的增大而增大。直径小于50 μm的水滴，其轨迹受重力的影响很小，可以忽略；当水滴直径超过50 μm时，重力的影响不能忽略。

(2)当水滴直径小于800 μm时，重力对局部水收集系数以及收集区域的影响很小，可以忽略。

(3)SLD极限轨迹的初始位置由于受重力的影响而出现不同程度的往上偏移，这为冰风洞设计中喷嘴安装位置的确定提供了指导；另外，SLD的撞击特性可为防冰系统的设计提供一定的参考。

[1]焦云涛.飞机积冰的危害与对策[J].民航经济与技术，1994，(7)：36—37.

[2]Addy Jr H E，Broeren A P，Zoeckler J G，et al.A Wind Tunnel Study of Icing Effects on a Business Jet Airfoil[R].AIAA 2003-727，2003.

[3]Tan S C，Papadakis M.General Effects of Large Droplet Dynamics on Ice Accretion Modeling[R].AIAA 2003-392，2003.

[4]Miller D，Ratvasky T，Bernstein B，et al.NASA/FAA/NCAR Supercooled Large Droplet Icing Flight Research:Summary of Winter 96-97 Flight Operations[R].AIAA 1998-577，1998.

[5]王梓旭.关于飞机结冰的水滴撞击特性计算与结冰相似准则[D].四川 绵阳：中国空气动力研究与发展中心，2008.

[6]裘燮纲，韩凤华.飞机防冰系统[M].第一版.北京：航空专业教材编审组，1985.

[7]王 波.涡轴发动机零级导叶热气防冰系统性的计算与实验研究[D].上海：上海交通大学，2007.