航空发动机高空模拟试验排气环境压力模糊控制技术研究
赵 涌,侯敏杰,张 松,彭 炬
(中国燃气涡轮研究院,四川 江油 621703)
1 引言
航空发动机高空模拟试车台是研制、测试航空发动机高空工作性能的大型地面设备,世界上仅有少数航空强国拥有此类设备并掌握其试验技术。我国拥有亚洲供抽气能力最大、种类齐全的航空发动机高空模拟试车台[1],其关键技术之一就是模拟排气环境压力的控制系统设计,该压力的模拟精度与发动机的试车安全和试验结果的有效性密切相关。目前,我国高空模拟试车台为避免高温、高速燃气对调节机构稳定工作的影响,将排气环境压力调节机构设置在距发动机出口较远位置。在发动机与调节机构间的这段腔体内,包含了众多的节流环节和换热设备,使得腔体内各特征截面气体总温、总压差别大,难以对该系统建立完备的数学模型。在高空模拟试车台进行航空发动机高空起动、高空推力瞬变等试验时,发动机状态的快速改变会引起燃气流量、总温、总压及排气扩压器效率产生快速变化,这些因素极大地干扰了发动机排气环境压力模拟精度。此时系统需要有足够快的反应速度在大范围内进行调整,才能满足压力过渡态控制要求,有效避免试车安全事故的发生。航空发动机高空稳态性能只有在排气环境压力“稳定不变”时才能“准确”测得,这要求系统降低对各种噪声的敏感度以提高其稳定性。对于不同航空发动机的不同环境压力和飞行马赫数,排气环境压力控制系统工况变化非常剧烈,其工作特性直接关系着发动机高空模拟试验的周期、成本和试验条件模拟的准确性。但由于发动机工作包线范围的宽广性和发动机功率状态变化的快速性,使得传统的PID控制算法很难实现在发动机工作包线范围内对其进行快速度和高精度的控制,且难以实现对各种情况的性能鲁棒性。因此,设计具有高精度、快速度、强抗干扰能力的排气环境压力控制系统是我国航空发动机高空模拟试验的迫切要求。
2 仿人工智能模糊控制分析
排气环境压力自适应模糊控制,是仿人工智能在线利用对偏差(e)和偏差变化率(Δe)的模糊规则及推理来调整PID算法中的控制参数[2]。系统采用模糊PID控制技术时,PID参数的整定不依赖于对象数学模型,且PID参数能够自动在线调整[3],以满足实时控制的要求。本文采用自适应模糊PID控制,自动调整控制算法控制参数,既能适应过程参数的变化,又具有常规PID控制的优点[4]。
模糊控制算法是将给定压力与反馈压力比较后的e及Δe进行模糊量化。模糊推理是把输入的模糊语言值作为推理条件,根据模糊规则进行推理,得出模糊输出值,再经反模糊化后得到精确的比例系数Kp、积分系数Ki和微分系数Kd。PID数字控制算法在接收到Kp、Ki和Kd后根据(1)式计算其准确的输出值:
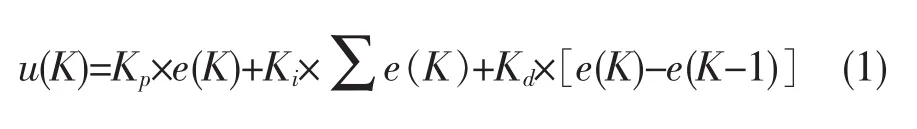
该输出值对应调节机构开度,改变调节机构所控制的气体流量,从而调节发动机环境压力使其逼近压力设定值。
模糊控制算法参数众多,必须通过多次修改模糊推理规则,并依据半物理仿真试验和真实试验的反复调试才能最后确定[5]。图1所示为排气环境压力调节过程,经仿人工智能分析[6],得出的模糊推理规则遵循以下原则:
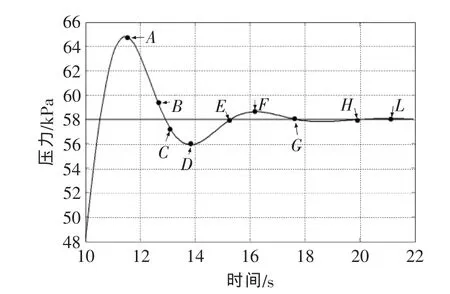
图1 排气环境压力阶跃响应Fig.1 The step response of exhaust pressure
(1)在偏差较大时(如图1中AB、CE段),为尽快消除偏差,提高响应速度,同时避免系统响应出现超调,Kp取大值,Ki取零。在偏差较小时(如图1中BC段),为继续减小偏差,并防止超调过大、产生振荡、稳定性变坏,Kp值要减小,Ki取小值。在偏差很小时(如图1中EL段),为消除静差,克服超调,使系统尽快稳定,Kp值继续减小,Ki值不变或稍取大。
(2)当偏差与偏差变化率同号时(如图1中CD、FG段),被控量朝偏离既定值方向变化,Kp取大值。在偏差较大且偏差变化率与偏差异号时(如图1中AB、DF、GH段),Kp取小值,以加快控制的动态过程。
(3)偏差变化率的大小表明偏差变化的速率,偏差变化率越大(如图1中BC段),Kp取值越小,Ki取值越大,反之亦然,同时结合偏差大小来考虑。
(4)微分作用可改善系统的动态特性,阻止偏差变化,有助于减小超调量,消除振荡,缩短调节时间。允许加大Kp值,使系统稳态误差减小,提高控制精度。所以,在偏差较大时(如图1中AB、CE段),Kd取零;偏差较小时,Kd取一正值,实行PID控制。
3 模糊控制系统设计
3.1 偏差及偏差变化率的模糊化
根据模糊理论及本系统特性,e、Δe的论域都为[-1 1]。 输出语言变量 K′p、K′i和 K′d的论域都为[0 1][7]。 对 e 变量定义 7 个模糊子集:NB(负大)、NM(负中)、NS(负小)、ZO(零)、PS(正小)、PM(正中)、PB(正大)。对 Δe变量定义 5 个模糊子集:NB(负大)、NS(负小)、ZO(零)、PS(正小)、PB(正大)。 隶属度函数均采用三角形全交迭函数,e的隶属关系如图2所示,Δe的隶属关系如图3所示。
3.2 控制参数的模糊规则
K′i根据e和Δe的隶属关系及相应模糊推理规则调整,其模糊规则见表1,三维查询图见图4。K′p和K′d的模糊规则及三维查询图相似于K′i。
本文通过航空发动机高空模拟试验环境压力半物理仿真试验及真实的高空模拟试验得到以上各参数取值。
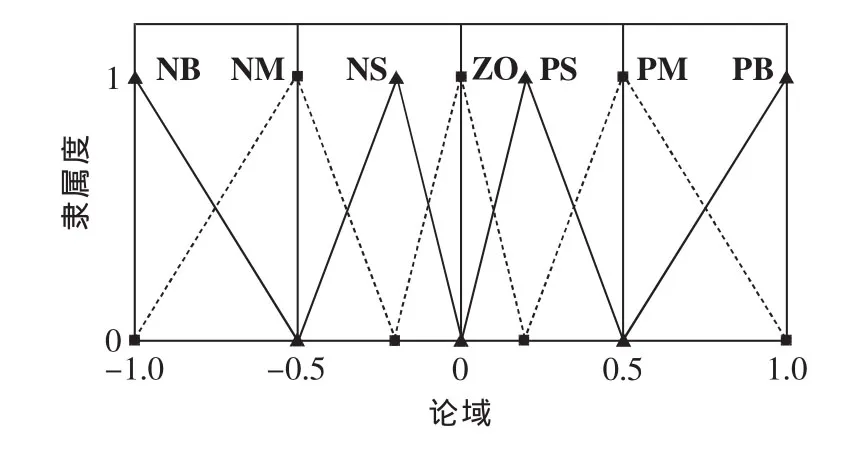
图2 e的隶属度函数Fig.2 The e membership function

图3 Δe的隶属度函数Fig.3 TheΔemembership function
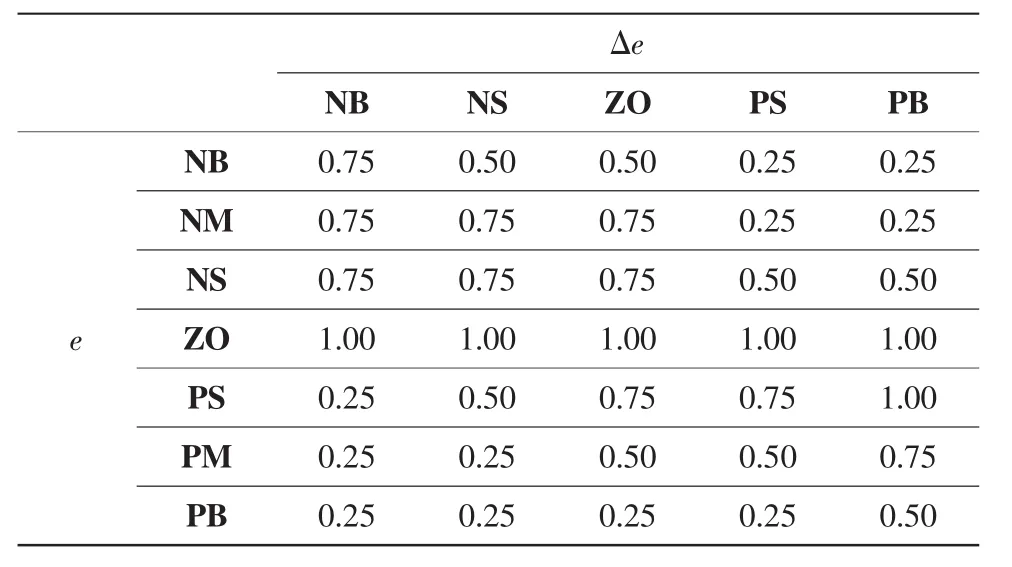
表1 K′i调整规则Table 1 The K′iadjusting regulation
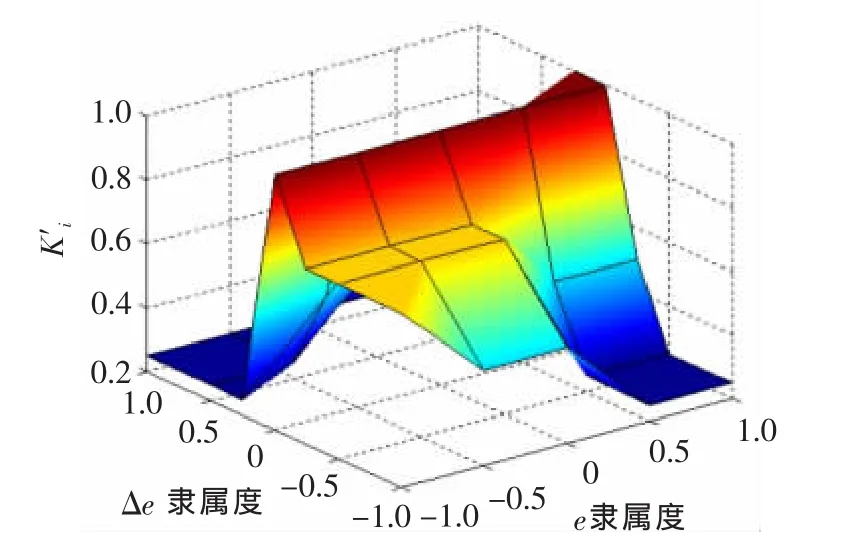
图4 K′i三维查询图Fig.4 The K′ithree-dimension query drawing
3.3 控制参数精确化
通过基本系数乘放大系数的方法和极大极小推理重心法[8]均可计算模糊输出Kp、Ki和Kd的精确值。本文采用极大极小推理重心法求Kp的精确值:
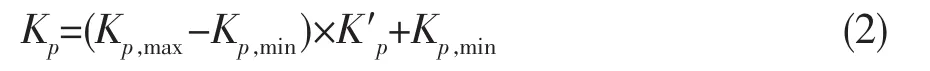
式中:Kp,max、Kp,min分别为 Kp的最大取值和最小取值。
模糊控制算法在PLC控制算法上具体实现时,可按表2编排系数偏移地址,用插值的方法在二维表格中找到四个位置相邻的K′p地址,分别为:

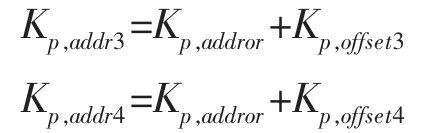
式中:Kp,addror为 K′p系数的起始地址;Kp,offset为 K′p系数的偏移地址。由表2可以看出,偏移地址值为e、Δe数字代号之和。
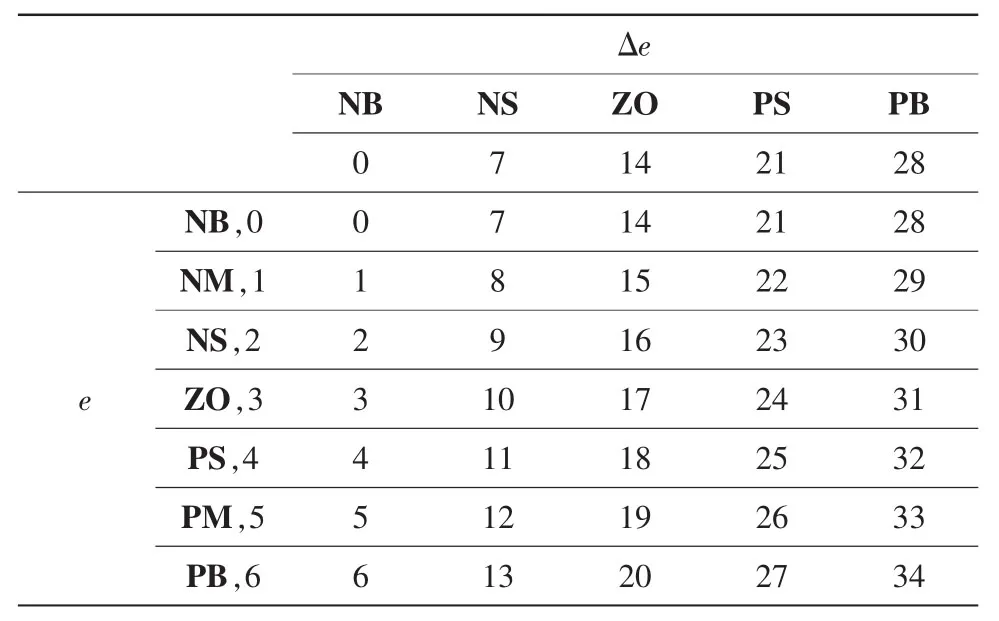
表2 Kp,offsetTable 2 Kp,offset
设所求点在 Kp,addr1与 Kp,addr2间,对 Kp,addr1的距离为 d1,对 Kp,addr2的距离为 1-d1;在 Kp,addr1与 Kp,addr3中,对 Kp,addr1的距离为 d2,对 Kp,addr3的距离为 1-d2,d1、d2均小于 1,大于 0。 K′p系数为[9]:
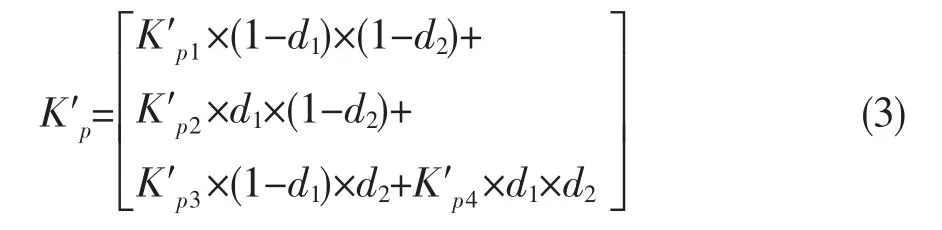
式中:K′p1、K′p2、K′p3、K′p4分别为地址 Kp,addr1、Kp,addr2、Kp,addr3、Kp,addr4所存数据。
其计算结果为K′p系数二维双线性插值结果,将K′p代入(2)式便可得 Kp的精确值。Kp的精确化过程计算量较小,有利于实现在线计算控制。Ki和Kd的精确化过程与Kp的相似。
4 试验结果分析
4.1 半物理仿真试验
高空模拟试验是高风险、高能耗的试验,因此在进行真实的联合调试前,应对高空模拟试车台模拟飞行包线上的边界点作大量的半物理仿真研究。在半物理仿真试验过程中,环境压力模糊控制系统与传统PID控制系统表现出了不同的调节品质。利用一组控制参数进行压力输入值突变与发动机状态变化扰动[10,11]的半物理仿真试验,试验结果如图5、图6所示,其中PLC控制系统(包括模糊控制算法)、调节机构及操作台等为真实物理部件,空气流量、排气环境压力为数学模型。
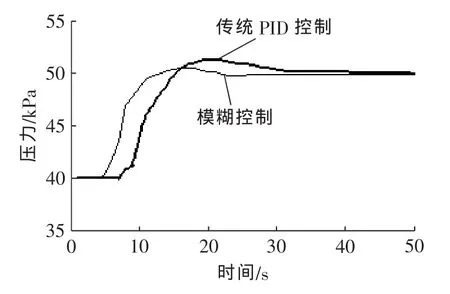
图5 传统PID与模糊控制阶跃响应对比Fig.5 The step response contrast of routine PID and fuzzy control
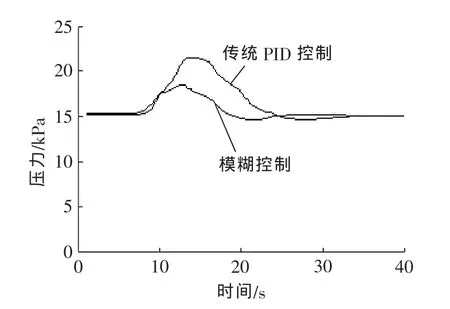
图6 传统PID与模糊控制抗扰动对比Fig.6 The anti-interference contrast of routine PID and fuzzy control
通过以上半物理仿真试验可以看出,在传统PID控制系统中引入模糊控制算法后,系统性能得到了改善。更重要的是,大量半物理仿真试验表明,系统在整个工作包线范围内都能可靠稳定工作,为真实的系统调试试验提供了依据。
4.2 高空模拟调试试验
以半物理仿真试验调试得到的最优参数作为初始值进行真实试验,并根据试验情况局部调整系统参数即可得到较理想的结果。原来需要多次试验、共计十几个小时才能完成的任务,在采用此种系统调试方法后仅两个小时就完成了试验。
图7显示了传统PID控制和模糊控制系统在受到相同强度扰动情况下排气环境压力调整、稳定的过程。如图中所示,模糊PID控制系统在受到扰动时,其Kp、Ki、Kd参数会自动根据压力偏差和偏差变化情况作在线调整。这种仿人工智能的控制参数在线调整,使得系统抗扰动能力得到增强,压力调节具有良好的跟踪性能,其调节时间缩短,超调量减小。
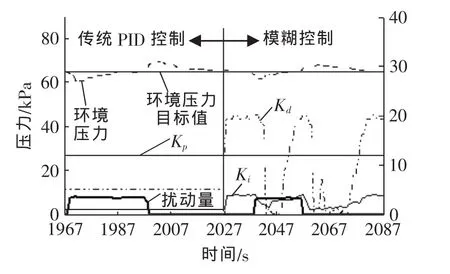
图7 模糊控制与传统PID控制抗扰动试验比较Fig.7 The anti-interference debugging test contrast of routine PID and fuzzy control
5 结论
从仿真试验和真实调试试验结果可以看出,模糊PID控制系统可以根据压力偏差及偏差变化率信号灵活地在线自整定控制参数。半物理仿真试验证明了系统在整个工作包线范围内均具有性能鲁棒特性,并初步找到了系统的最优参数;真实试验结果证明了环境压力模糊控制系统具有良好的动态性能和控制精度,符合系统设计要求。这种先进行半物理仿真试验再进行高空模拟调试试验的方法,有效地减少了系统改进风险和系统调试时间,节约了成本,是在目前技术能力与硬件资源条件下,实现我国航空发动机高空模拟试验排气环境压力高品质模拟的有效途径之一。
[1]侯敏杰,陈建民,徐 国,等.先进航空动力崛起的基石——高空台[C]//.中国航空学会2007年学术年会动力专题.四川 江油:中国燃气涡轮研究院,2007.
[2]赵付舟,杨海青,魏民祥.发动机台架试验的模糊PID控制算法的仿真与研究 [J].机电工程技术,2005,34(12):41—43.
[3]Wang D J.Further Results on the Synthesis of PID Controllers[J].IEEE Transactions on Automatic Control,2007,52(6):1127—1132.
[4]孟庆明.自动控制原理 [M].北京:高等教育出版社,2003.
[5]Karayan V,Sander S,Cageao R.Soft Real-time PID Control on a VME Computer[R].NASA Tech Briefs,2007.
[6]吴 胜.人工智能[M].北京:电子工业出版社,2007.
[7]Ho H F,Wong Y K,Rad A B.Direct Adaptive Fuzzy Control for a Nonlinear Helicopter System[J].Aircraft Engineering and Aerospace Technology,2008,80(2):124—128.
[8]黄向华,彭召勇.无人驾驶直升机发动机模糊自适应PID 控制[J].航空动力学报,2005,20(3):11—18.
[9]Sun C C,Wu S M,Chung H Y,et al.Design of Takagisugeno Fuzzy Region Controller Based on Rule Reduction,Robust Control, and Switching Concept[J].Journal of Dynamic Systems,Measurement&Control,2007,129(2):163—170
[10]谢光华,孟 丽,薛 恩,等.液体冲压发动机控制系统半实物仿真[J].推进技术,2001,22(6):10—13.
[11]Zhang H S,Su M,Weng S L.Hardware-in-the-loop Simulation Study on the Fuel Control Strategy of a Gas Turbine Engine[J].Journal of Engineering for Gas Turbine and Power,2005,127(3):693—695.

