高拱坝体型三维拓扑优化研究

苏 超,孙 蓓

(河海大学水利水电学院,江苏南京 210098)

国内以往拱坝优化设计研究主要以工程应用为主[1-2],针对给定的多种体型进行参数优化设计[3],尚处于形状优化阶段,对拱坝的结构布局并没有较先进的系统理论支持.结构拓扑优化属于布局优化[4],是结构优化中较难的一个层次.与传统的优化设计不同,拓扑优化不需要给出目标函数、状态变量和设计变量等参数优化变量,而只要给出结构的材料特性、模型、荷载等,其优化的潜力更巨大,更富挑战性.以连续体为初始结构的拓扑优化,由于较少依赖对分析对象的已有知识,方法更具一般性,受到愈来愈广泛的重视.运用拓扑优化进行结构优化设计,是结构优化领域的发展趋势.本文应用三维拓扑优化理论并结合高拱坝结构特点,尝试对高拱坝三维空间结构进行建模和优化设计.

1 基本理论和条件

1.1 拓扑优化均匀化方法

拓扑优化基于有限元法[5-6](FEM),均匀化方法[4,7-8]就是在传统FEM基础上,将整个设计空间假设成类似“气孔分布”的微结构单元(单胞),单胞在优化开始前分布均匀,而且大小全部相同.在拓扑优化过程中,单胞密度分布产生变化:密度在高负荷区域变大,在低负荷区域变小.优化过程类似于自然的细胞结构,在优化过程中形成一种承重结构,这种结构在高应力区域气孔“密集”,在低应力区域气孔密度较低.如果定义一个合理的密度最小值,然后剔除设计空间中低密度负荷区域,就将产生一个材料效应最高的重量优化承重结构.

以微结构单胞的几何尺寸及方位角为设计变量,通过某种优化算法,确定结构的某种性能指标达到最优设计时设计区域各处的材料密度分布,从而可以确定最优解.本文选用常用的准则法作为优化算法配合结构拓扑优化计算.

图1给出了使用均匀化方法进行结构拓扑优化的流程.

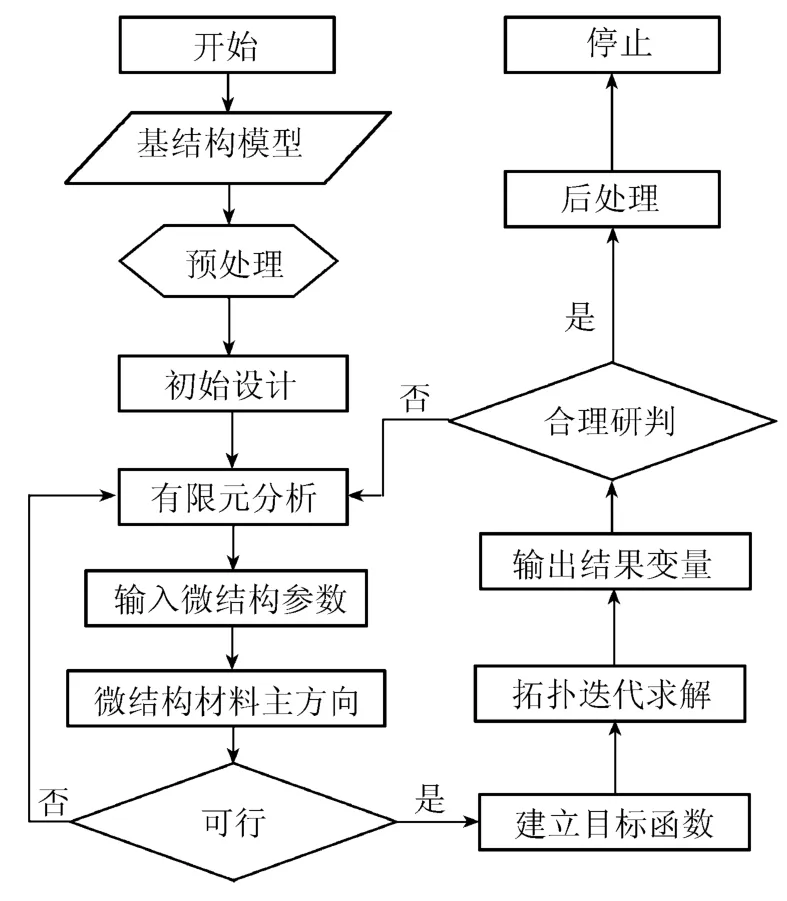
图1 结构拓扑优化流程Fig.1 Flow chart of structural topology optimization

拓扑优化均匀化方法的数学模型[9]为

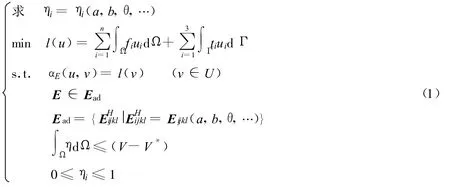
式中:a,b,θ——微结构尺寸参数;ηi——微结构单元单胞的密度;l(u),l(v)——结构柔顺度泛函;Ω——设计区域;fi——结构所受到的节点等效体积力;ti——结构所受到的节点等效边界荷载;ui——节点位移;u——结构位移;v——给定的位移场;U——结构整体位移;αE(u,v)——结构的应变能;E——结构材料弹性张量;Ead——允许的结构弹性张量集合;EHijkl——均匀化的复合材料弹性张量;V——结构初始体积;V*——指定去除的材料的体积.

1.2 数值不稳定现象的处理

拓扑优化常出现的数值不稳定现象[9-11]为棋盘格式、网格依赖性及局部极值现象.结构拓扑优化等价于一个偏微分方程的反问题,由于其解的不适定性,使得结构优化后容易出现一种数值不稳定现象——棋盘格式.而结构拓扑优化问题的解虽然是不适定的,但其解之间却存在一定的联系,当采用不同的方式对积分方程进行离散化时,所得的数值解是不会稳定的,而且常常是网格划分越细,所得到的线性代数方程组的矩阵条件数越大,解就越不稳定,因此又导致了网格依赖性现象的出现.除此之外,局部极值现象也常常使得拓扑计算很难得到全局最优解.

拱坝受力条件复杂,有多种受力状态.虽然棋盘格式等数值不稳定现象出现的直接原因和结构的受力没有很大的关联,但事实证明,结构的边界条件越复杂,受力种类和形式越多,就会使数值不稳定现象越明显,对结构的最终拓扑形式的影响也越大.为了避免出现优化结果没有实用价值的现象出现,必须解决数值不稳定现象问题.

本文采用滤波法同时处理棋盘格式和网格依赖性误差的高通部分,采用多重网格法处理网格依赖性误差的低通部分,即综合使用多重网格法和滤波法解决网格依赖性问题,利用滤波半径延拓方法一定程度上解决局部极值问题.

2 拱坝拓扑优化算例

2.1 基本条件

某双曲拱坝,坝高113m,上游承受109.2m的水头,下游承受水头为20m,上、下游水位落差为89.2m.坐标系采取笛卡儿坐标系,x轴从左岸指向右岸,y轴指向上游,z轴铅直向上.坝体混凝土密度2400kg/m3,弹性模量24GPa,泊松比0.167.

拱坝基岩尺寸为沿坝体左、右岸各延伸约300m,深度也为300m.计算工况只取基本载荷组成(正常蓄水位以及自重).由于坝体上游面直接承受水荷载,若直接参与拓扑优化,计算量过大且难以得到满意的结果,因此,基岩部分和坝体上游面不参与拓扑优化计算,坝体拱圈断面上游曲线采用一般二次曲线.基岩密度2850kg/m3,弹性模量30GPa,泊松比0.25.水密度1000kg/m3.

图2显示了包含基岩和坝体的整体拱坝基结构有限元网格.由于模型较大,坝体部分比较模糊,为更加直观,图3单独显示坝体部分的有限元基结构.

体积删除率选择为40%,迭代20次.

按照SL 282—2003《混凝土拱坝设计规范》要求,拱坝整体结构的强度条件设定为 σ1≤1.2MPa,σ3≥-9.0MPa.

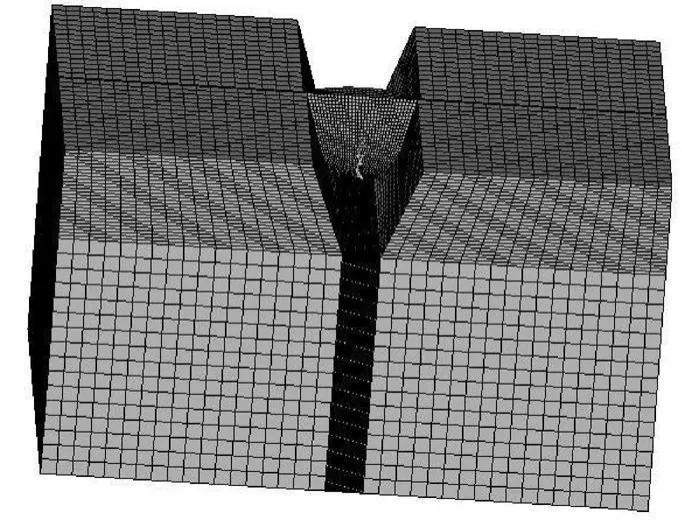
图2 拱坝基结构模型Fig.2 Basic structural model of arch dam

图3 局部坝体基结构模型Fig.3 Basic structural model of local part of arch dam

2.2 拓扑优化计算结果

图4为拓扑优化局部结果,结果显示为保留单胞密度为0.6～1.0的单元.由于基岩部分不在优化范围内,图4给出保留少部分基岩时,拱坝拓扑优化结果.从图4可以看出:拱坝从下游面开始,沿着坝体厚度方向,依照各结点单元荷载情况,逐步删除应力较小的单元,层层推进,趋势十分明显;整个拱坝由坝底向坝顶方向,逐渐变薄,拱坝坝体的下游为一曲面.

图4 拓扑优化局部结果Fig.4 Local results of topology optimization

3 拱坝拟合结果

拓扑优化计算的结果并不适合直接在工程上应用,必须对拱坝下游的曲面进行适当的光滑拟合,才能在工程上得以实现.

对图4所示的拱坝优化结果进行下游面光滑拟合,得到的拱坝坝体有限元模型如图5(a)所示.为清晰表示拟合结果,图5(b)和图5(c)分别给出坝高45m处水平拱圈及拱冠梁拟合结果.

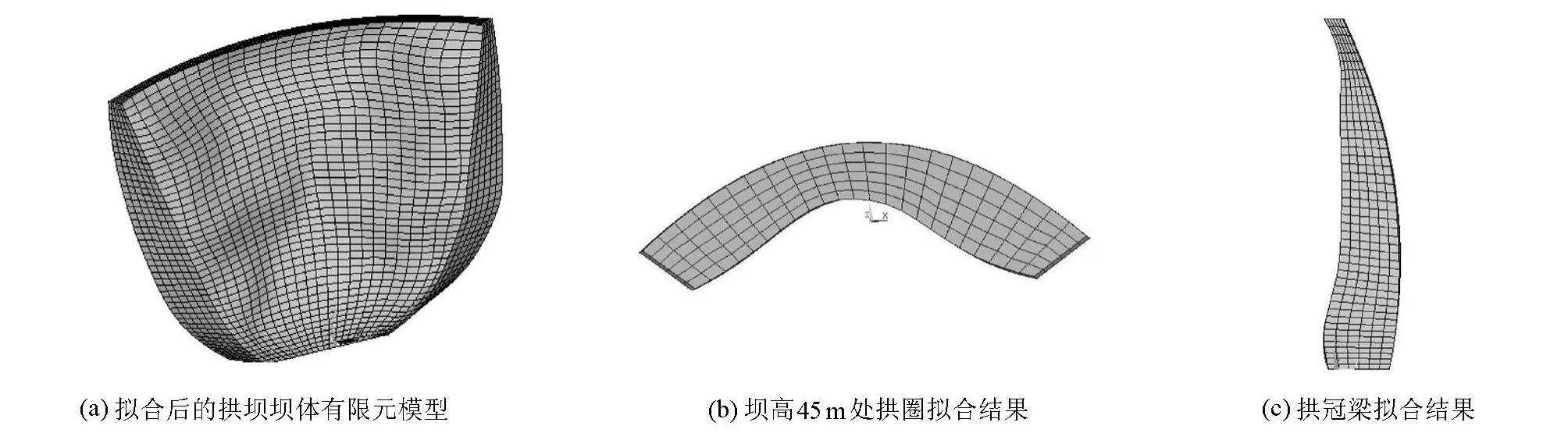
图5 经拟合得到的拱坝结果Fig.5 Fitting results of arch dam

4 拟合结果应力校核

对该拟合拱坝进行了应力校核.校核结果表明,最大值为1.11MPa＜1.20MPa,第3主应力最小值为-8.86MPa＞-9.00MPa,符合SL 282—2003《混凝土拱坝设计规范》要求.但是,在坝踵处存在应力集中问题,需要引起重视并采取适当方式进行处理.

5 结 语

结构拓扑优化能在工程结构设计的初始阶段为设计者提供一个概念性设计,使结构在布局上取得较优方案,与尺寸优化和形状优化相比更具有一般性.本文对拱坝的基岩和荷载进行适当简化,采用均匀化方法对其进行了结构拓扑优化计算,这一尝试取得了初步成功,所得的拱坝体型与常规认识基本一致,强度满足应力强度要求.但由于考虑的荷载作了相应的简化,没有考虑温度的影响,其实用性还需进一步研究.

[1]苏超,余天堂,姜弘道.基于有限单元法的高拱坝动力优化设计方法及其应用[J].河海大学学报:自然科学版,2002,30(1):1-5.(SU Chao,YU Tian-tang,JIANG Hong-dao.FEM-based dynamic optimum design methodfor high arch dams and its application[J].Journal of Hohai University:Natural Sciences,2002,30(1):1-5.(in Chinese))

[2]孙林松,王德信,裴开国.以应力为目标的拱坝体型优化设计[J].河海大学学报:自然科学版,2000,28(1):57-60.(SUN Lin-song,WANG De-xing,PEI Kai-guo.Stress-oriented shape optimization of arch dams[J].Journal of Hohai University:Natural Sciences,2000,28(1):57-60.(in Chinese))

[3]陈忠,谢能刚,王璐.基于模糊理论的高拱坝多目标优化设计[J].河海大学学报:自然科学版,2009,37(3):330-334.(CHEN Zhong,XIE Neng-gang,WANG Lu.Multi-objective shape optimization design of high arch dams based on fuzzy theory[J].Journal of Hohai University:Natural Sciences,2009,37(3):330-334.(in Chinese))

[4]BENDEOE M P,KIKUCHI N.Generating optimal topologies in structural design using a homogenization method[J].ComputerMethods in AppliedMechanics and Engineering,1988,71(2):179-224.

[5]BENDEOE M P,R ODRIGUES H C.Integrated topology and boundary shape optimization of 2-D solids[J].Computer Methods in Applied Mechanics and Engineering,1991,87(1):15-34.

[6]SUN K H,CHO S H,KIM Y Y.Topology design optimization of a magnetostrictive patch for maximizing elastic wave transduction in waveguides[J].IEEE Transactions onMagnetics,2008,44(10):2373-2380

[7]GUO X,CHENG G,YAMAZAKI K.A new approach for the solution of singular optima in truss topology optimization with stress and local buckling constraints[J].Structural andMultidisciplinary Optimization,2001,22(5):364-372.

[8]孙蓓.连续体结构拓扑优化理论研究及其在水利工程中的应用[D].南京:河海大学,2005.

[9]刘震宇.微型及小型柔性机械结构的拓扑优化设计方法[D].大连:大连理工大学,2000.

[10]SIGMUND O,PETERSSON J.Numerial instabilities in topology optimization:a survey on procedures dealing with checkerboards[J].Mesh-dependancies and LocalMinima,Structural Optimization,1998,16:68-75.

[11]DIAZ A R,SIGMUNDND O.Checkerboard pattems in layout optimization[J].Structural and Multidisciplinary Optimization,1995,10(1):40-45.