基于应变状态的岩石损伤演化模型

张 莱,陆桂华

(河海大学水文水资源学院,江苏南京 210098)

岩体损伤的宏观和细观研究均表明,由局部应力集中或局部变形不协调引起的损伤局部化是节理岩体损伤的一个重要特征[1-4].很多学者对损伤局部化进行了研究:周小平等[5]研究微裂纹方位角为Weibull分布和微裂纹长度的分布密度函数为Rayleigh函数时对损伤局部化影响;刘元高等[6]采用概率统计方法分析节理裂隙岩体的几何特征,定义了反映节理裂隙岩体几何特征的组构张量;赵吉东等[7]提出一种包含应变梯度项的损伤力学模型,并将其应用于材料的局部化损伤模拟预测中.基于几何特征统计的损伤张量难以描述节理岩体损伤局部化现象[8],因此亟须建立一种基于应力或应变等力学参量的损伤张量来描述这种损伤局部化现象.本文基于材料的应变状态建立损伤张量,并根据弹脆性本构关系和相应的屈服准则推导损伤演化方程,以研究岩石材料的损伤效应.

1 一维损伤变量及损伤演化方程

引入Lemaitre损伤变量

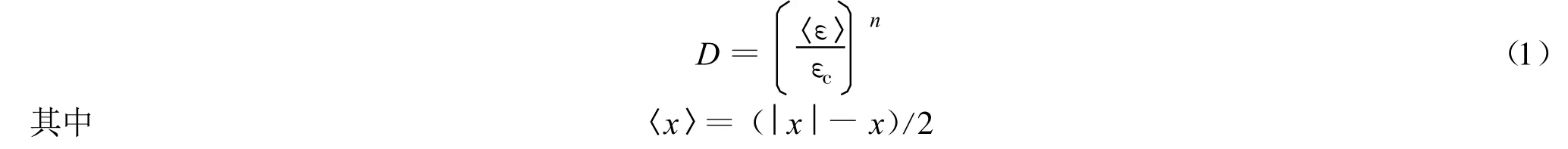
式中:D——一维损伤变量;ε——轴向应变;εc——包含残余应变的容许值;n——表征材料脆性的参数,n越大,材料脆性越强.

观察损伤张量的定义,损伤状态与应变状态相关,损伤的演化取决于应变状态的变化,应变状态的变化又与损伤状态有关.一维状态的损伤演化方程可以在主应力空间扩展到三维.如图1所示,εc为当n→∞时的弹性应变上界值,包括破坏前应变和破坏后的残余应变.

对于脆性岩石材料而言,在裂纹尖端的局部区域内,可能不会出现塑性屈服,而是脆性破坏后的微小碎末区域包含在未破坏的完整岩石之中.因此在描述损伤演化的时候不能认为岩石破坏后仍然具有承载的能力,残余应变也就无从谈起.式(1)的εc应当去除残余应变.去除残余应变后的残余应变容许值就等于峰值应力对应的应变.因此,采用最大拉应变准则来判定材料是否破坏是合适的.

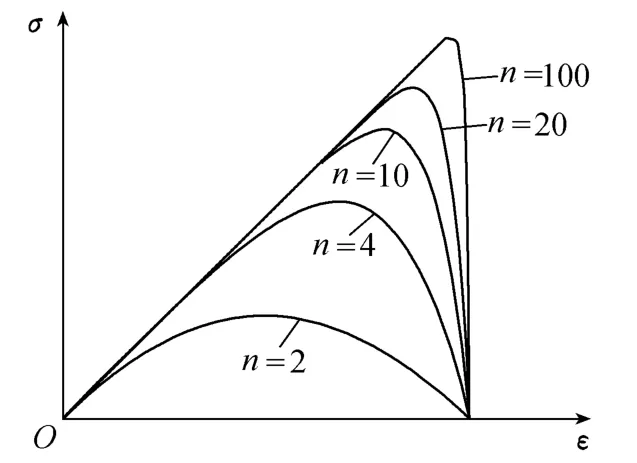
图1 损伤材料的应力应变关系[9]Fig.1 Relationship between stress and strain for damaged materials[9]

临界状态为

式中:ε——应变分量;εc——容许拉应变.当ε=εc时,材料破坏.εc取单轴拉伸试验的极限破坏应变.

2 三维损伤变量及演化方程

试验表明,混凝土材料在单轴压缩时的损伤是张应力引起的,损伤方向与载荷方向正交,这表明混凝土的损伤是各向异性或正交各向异性的[10].坚硬岩石材料与混凝土材料性质相似,可以认为岩石材料的损伤是正交各向异性的.在主应力空间,假定应力主轴、应变主轴和损伤主轴互相重合.材料初始状态是各向同性线弹性体,损伤后表现出正交各向异性性质.在此假定下,损伤张量D和应力张量σ均为二阶张量.设3个主损伤分量为D1,D2,D3,则根据热力学第二定律、一维损伤的定义式(1),(2)及损伤变量的物理意义,有

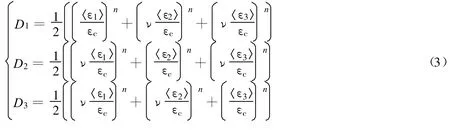
式中ν为泊松比.

在单轴压缩状态(σ1＞0,σ2=σ3=0),有 ε1＞0,ε2=ε3=ε′,ε′＜0,则式(3)变为

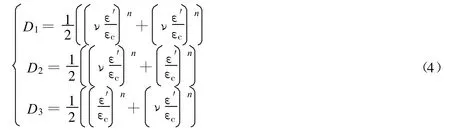
从岩石试件的单轴压缩试验观察到,试件破坏的方向大体与压应力方向一致.这与式(4)D1＜D2=D3相符.另外,按式(4)σ3方向也有损伤.这是因为当微裂纹出现后,微裂纹的方向并不完全是破坏时的宏观裂纹方向,初始微裂纹的方向存在一定的随机性,这也正是D1的含义.在数量上,D1远远小于D2和D3.这从图2D1和D2的敏感性曲线可明显看到.

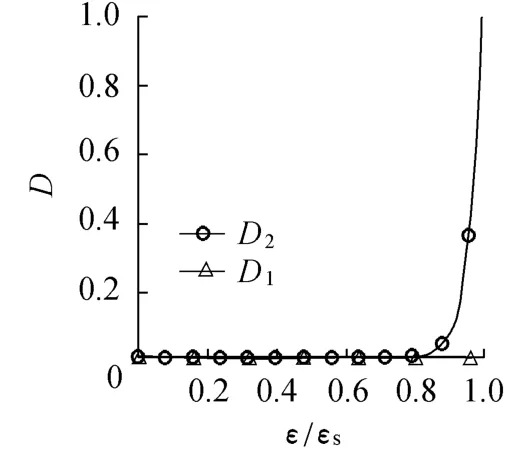
图2 D1与D2的敏感性曲线Fig.2 Sensitivity curves for D1and D2

3 弹脆性材料损伤本构方程

无损状态下柔度矩阵为

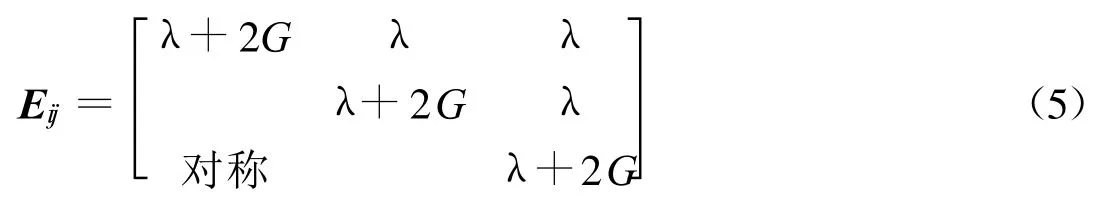
式中λ,G为拉梅常数和剪切模量:

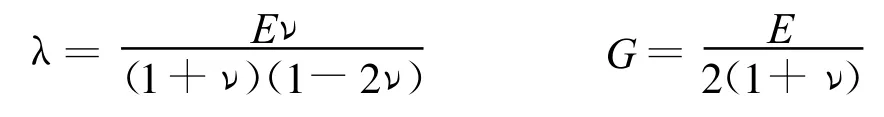
因此在主应力方向上有

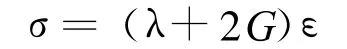
根据Sidoroff提出的能量等价原理[11],对损伤材料,柔度张量˜Eij为

式中Eij为无损弹性张量.考虑式(5)及式(6),得

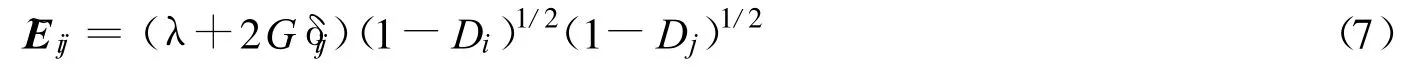
则由广义虎克定律及式(7)推出弹脆性损伤材料的本构关系为

式中:σ1,σ2,σ3——3 个主应力分量;ε1,ε2,ε3——主应变分量;D1,D2,D3— —相应于 3 个主应力方向的损伤分量;E——弹性模量.因为D1≠D2≠D3,因此共5个独立变量.

4 计算实例

在PowerStationV4.0平台上编制了水力劈裂有限元程序的力学模块FEM3_Damage.f 90.选用的计算实例模型尺寸为S×W×B=40cm×10cm×5cm的混凝土三点弯曲梁[12],在上侧中点处作用一集中力P,计算简图与网格剖分见图3.有关的力学参数如下:D0=0.048,E0=32.7GPa,ν=0.167,n=25.

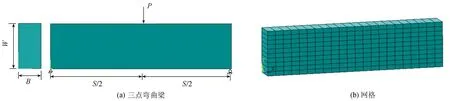
图3 三点弯曲梁及网格Fig.3 Three-point bending beams and grids

模型共划分220个单元,506个节点.在两端下角点铰接约束.施加载荷P=6.25kN,分25个载荷步,逐渐加载.荷载步选为0.25kN,即 ΔP=0.25kN.P=2.75kN(第 11步),P=4.0kN(第16步)和P=6.0kN(第24步)时水平方向的应力场见图4.图5为在ANSYSR5.5平台计算得到的不考虑损伤时的弹性水平应力场(加载P=6.25kN).

为验证损伤模型,取文献[9]的损伤模型(演化方程),编入同一计算程序,同时计算,并考察计算结果,以作比较.

图4(b)与(e)相比可见,在P=4.0kN时在梁的底部,图4(e)的水平应力已出现不连续,说明本文模型在计算中出现损伤要迟于文献[9]的模型.而一旦损伤出现,便很快破坏.水平应力的不连续性,是受损伤产生的裂缝的影响.从图4两个模型的比较可见,在载荷较小时,本文模型的极限水平应力与文献[9]模型相当(图4(a)与(d)),并随着载荷的增加,极限应力水平从略小于文献[9]模型(图4(b)与(e))到差别有增大的趋势(图4(c)与(f)).这意味着本文模型有更快的损伤演化速度,这正是脆性岩石的性质.

图6表示损伤出现在梁下部受拉区域,说明遵循最大拉应变破坏准则的损伤变量能够比较准确地描述3点弯曲梁损伤发展的状态.梁端的损伤是因为考虑3个方向应变的损伤演化方程,应变分量对损伤变量具有交叉贡献.

图7为文献[9]模型和本文模型计算得到的梁纵向位移的曲线,可见本文模型纵向位移略大.这与图4(c)与(f)最大水平应力的比较是一致的.本文模型计算得到的损伤要大于文献[9]的损伤,导致梁的刚度较小,因此挠度较大.但是差别值很小,2个模型计算结果是接近的.

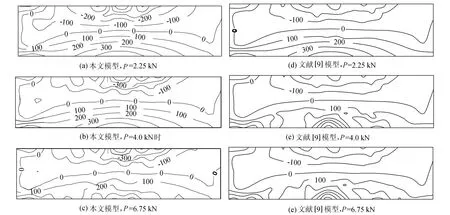
图4 各载荷步水平向应力等值线(单位:kPa)Fig.4 Contours of horizontal stress for various loading steps

图5 不考虑损伤的水平向应力(用ANSYSR5.5计算,单位:kPa)Fig.5 Horizontal stress without consideration of damage(calculated by ANSYSR 5.5)

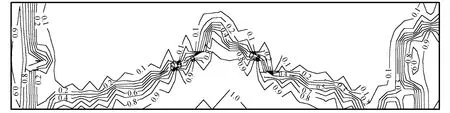
图6 第22步(P=5.5kN)时的损伤变量Fig.6 Damage variables at 22ndstep(P=5.5kN)

5 结 论

岩石的破坏,单就力学效应来讲,是岩石受力超过其所能承受的最大值,岩石破裂.岩石破裂的直接原因是应变超过极限值,岩石内部从局部开始产生微裂纹.微裂纹的扩展和相互连通使得损伤增强,并且进一步增强损伤的局部化,直至形成宏观裂纹,最终导致岩石破坏.

但是,当岩石被作为均匀介质时,基于统计方法的损伤力学很难真实描述岩石损伤的局部化现象.本文基于应变的损伤变量与有关模型的相关损伤模型比较,损伤的发展越快,也就越适合于描述岩石的脆性性质.

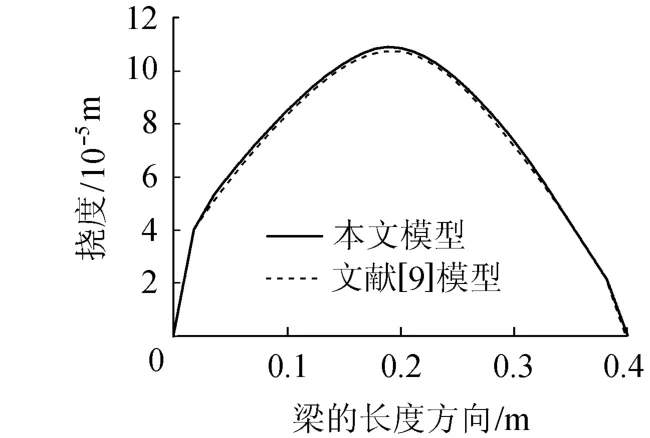
图7 三点弯曲梁挠度的比较Fig.7 Comparison among of deflections of three-points bending beams

岩石损伤的最后结果是岩石断裂破坏,基于连续介质力学体系的损伤力学还不能准确描述岩石的断裂过程以及断裂状态.将损伤和断裂理论相结合来研究岩石的破坏过程还有待于深入研究,损伤因子和断裂指标的结合以及由损伤到断裂的物理机制是断裂损伤联合研究的重点,也是难点.

[1]HORRI H,NEMAT-NASSER S,Brittle failure in compression:splitting,failure and brittle ductile transition[J].Phil Trans Royal Soc London:A,1986,319:337-374.

[2]宋飞,赵法锁,李亚兰.一种岩石损伤流变模型及数值分析[J].水利水电科技进展,2008,28(1):12-15.(SONG Fei,ZHAO Fasuo,LI Ya-lan.Damage rheological constitutive model for numerical simulation to gypsum breccias[J].Advances in Science and Technology of Water Resources,2008,28(1):12-15.(in Chinese))

[3]杨圣奇,徐卫亚,韦立德,等.单轴压缩下岩石损伤统计本构模型与试验研究[J].河海大学学报:自然科学版,2004,32(2):200-203.(YANG Sheng-qi,XU Wei-ya,WEI Li-de,et al.Damage rheological constitutive model for numerical simulation to gypsum breccias[J].Journal of Hohai University:Natural Sciences,2004,32(2):200-203.(in Chinese))

[4]浦奎英,范华林.流变损伤模型及其应用[J].河海大学学报:自然科学版,2001,29(增刊1):17-20.(PU Kui-ying,FAN Hualin.Rheological damage model and its application[J].Journal of Hohai University:Natural Sciences,2001,29(S1):17-20.

[5]周小平,王建华,张永兴,等.单轴拉伸条件下细观非均匀性岩石损伤局部化和应力应变关系分析[J].应用数学和力学,2004,25(9):943-950.(ZHOU Xiao-ping,WANG Jian-hua,ZHANG Yong-xing,et al.Analysis of the localization of damage and the complete stress-strain relation for mesoscopic heterogeneous rock under uniaxial tensile loading[J].AppliedMathematics and Mechanics,2004,25(9):943-950.(in Chinese))

[6]刘元高,周维垣,赵吉东,等.裂隙岩体损伤局部化破坏分岔模型及其应用[J].力学学报,2003,35(4):411-417.(LIU Yuangao,ZHOU Wei-yuan,ZHAO Ji-dong,et al.Discontinuous bifurcation model of damage localization for jointed rocks and its application[J].Acta Mechanica Sinica,2003,35(4):411-417.(in Chinese))

[7]赵吉东,周维垣,刘元高.基于应变梯度的损伤局部化研究及应用[J].力学学报,2002,34(3):445-452.(ZHAO Ji-dong,ZHOU Wei-yuan,LIU Yuan-gao.On the strain-gradient-enhanced damage modeland its application to the localization analysis[J].Acta Mechanica Sinica,2002,34(3):445-452.(in Chinese))

[8]谢和平.石混凝土损伤力学[M].北京:中国矿业大学出版社,1990.

[9]周维垣,剡公瑞,杨若琼.岩体弹脆性损伤本构模型及工程应用[J].岩土工程学报,1998,20(5):54-57.(ZHOU Wei-yuan,YAN Gong-rui,YANG Ruo-qiong.Elasto brittle damage model for rockmass based on field tests in Laxiwa arch dam site[J].Chinese Journal of Geotechnical Engineering,1998,20(5):54-57.(in Chinese))

[10]余天庆,钱济成.损伤理论及其应用[M].北京:国防工业出版社,1994.

[11]安民,俞茂宏,吴熹,等.广义双剪屈服准则在岩石力学中的应用[J].岩土力学,1991,12(1):17-26.(AN Min,YU Mao-hong,WU Xi,et al.Generalized twin shear stress yield criterion in rock mechanics[J].Rock and Soil Mechanics,1991,12(1):17-26.(in Chinese))

[12]邓爱民,符晓陵,徐道远.混凝土拉、压损伤的等价关系研究[C]//崔京浩.第十届全国结构工程学术会议论文集:第Ⅰ卷.北京:中国力学学会,2001.