五能级Ξ型原子系统相位消相干的Bang Bang控制
王艳辉,许迈昌
(1.湖南科技大学 物理学院,湘潭 411201;2.湖南工程学院 理学院,湘潭 411104)
量子系统和环境的相互作用是导致量子噪声的一个重要原因,量子噪声使得量子系统用以进行量子计算和量子信息处理的量子态的纠缠性和相干性被破坏,因而量子噪声抑制是量子信息与量子计算的发展以及量子计算机实现急需解决的一个问题[1].动力学解耦的方法,也称BangBang(BB)控制的方法,就是一种有效的对量子噪声抑制的方法.动力学解耦方法最初的工作起源于量子平均场效应思想,即1968年Haeberlen和Waugh用脉冲序列控制系统的有效哈密顿量[2].随后它被发展成核磁共振技术中的解耦和重聚焦技术[2,3].在这种思想启发下,Viola和Lloyd引入了动力学解耦方案,用动力学的方法压制单量子比特的消相干,从而保持量子系统态的相干性[4].我们前期的工作已经研究了二、三、四能级原子在一般噪声环境下的BB解耦问题以及任意能级型原子振幅消相干的BB解耦问题[5-8],这里我们研究五能级型原子相位消相干的BB解耦问题.
1 量子系统和环境相互作用的哈密顿量
整个系统Sab由原子Sa和原子所处的环境即热库Sb组成.令五能级 型原子的能级由低到高能级分别为|0〉、|1〉、|2〉、|3〉、|4〉.上能级|i〉(i=1,2,3,4)通过频率为对应的共振频率ωi i-1的激光场分别和它们相邻的低能级|i-1〉相互耦合.
我们把能级的本征值标为 Ei(i=0、1、2、3、4),有,为能级间的可能跃迁.在Hilbert空间 ,态矢|i〉(i=0、1、2 、3 、4)可表示为一个五列的的行矢,其中非零位为1,且前面共有i位,全为零,后面位也为零,即|i〉=(0 … 0 1 …).定义


2 动力学解耦机制[7]
动力学解耦方法使用共轭BB脉冲来过滤系统和环境整个哈密顿量中我们不想要相互作用部分,从而实现对量子系统的动力学行为进行控制,对系统量子噪声进行消相干抑制.BB脉冲是受控的幺正脉冲,相当于具有任意大的强度的脉冲操作,我们可以在忽略的时间t内开启或关闭它.
由于受环境的相互作用,原子系统在噪声作用下的自由演化哈密顿量为 H′=H+H I.在整个系统Sab上重复地循环地进行一系列BB控制操作V={Vk},(k=0,…,│V│-1),操作间都间以系统的自由演化.通过恰当的选择操作集V={vk},我们可以达到消除系统的自由演化哈密顿量H′中我们不想要的部分H 1,即实现了使系统和环境解耦的目的,成功地抑制了系统噪声.
考虑一个完整的循环.令U(△t)=exp(-i△t H′)为在循环中系统的自由演化,持续时间为△t=t(N│V│)-1.恰当选择解耦操作,使得它满足解耦条件

在解耦脉冲序列的作用下,单个循环时间Tc中复合系统的演化可以由算符
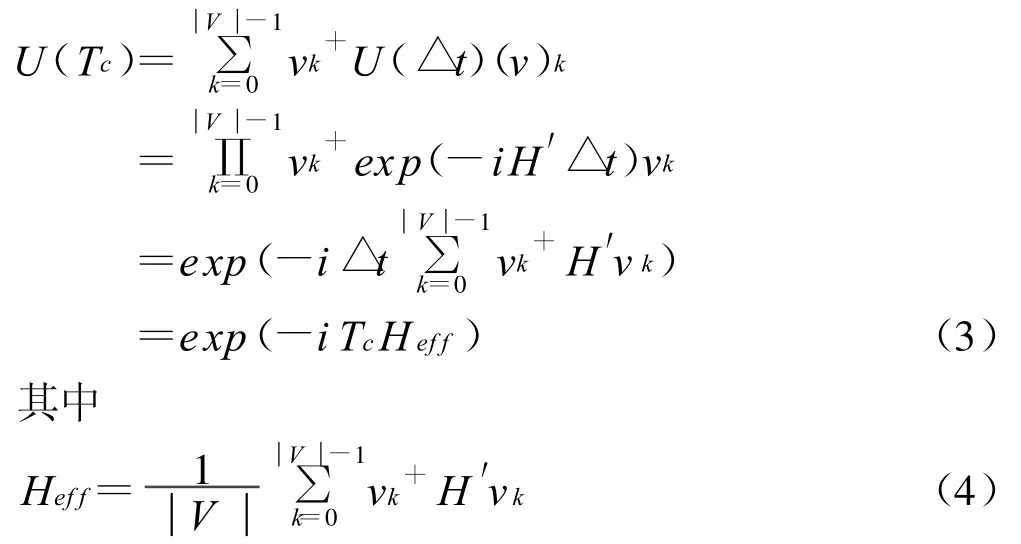
是系统Sab在运用解耦操作后的有效哈密顿量.在理想的极限情况Tc→0、重复的循环操作次数 N→∞下,系统运用了解耦操作脉冲序列之后的演化为U意味着我们已经从系统的整个哈密顿量H′中成功地消除了我们不想要的哈密顿量 ,从而成功地解除了系统和环境的相互作用.
3 五能级型原子相位消相干的BB解耦方案
从上节分析可知,要给出解耦方案,最主要的是要找出解耦操作集合.对于处于相位噪声环境的五能级型原子,我们发现解耦操作集为 ,其中 为五阶单位算符,其中为五阶单位算符,

4 解耦操作的脉冲实现
我们知道作用于原子上频率为共振频率 ωii-1(i=1,2,3,4)、作用时间为π/2的脉冲操作有如下的形式


因而解耦操作{V0、V1、V2、V3、V4}可以分解为如下的脉冲操作

为先作用一个与3、4能级共振的脉冲,其作用时间为π/2,然后作用一个与2、3能级共振的脉冲,其作用时间为π/2,继之以与2、1能级共振的脉冲和与1、0能级共振的脉冲,其作用时间均为π/2.而v2=v1◦v1,v3==,故五能级原子相位消相干抑制的解耦操作均可用π/2脉冲实现.
5 总结
我们给出了五能级型原子系统相位消相干抑制的BangBang解耦方案,包括了具体的解耦操作集合以及脉冲的物理实现形式.分析表明,在理想的脉冲情况下,所给的解耦脉冲能很好的压制五能级 型原子的相位噪声.
作者感谢低维量子结构与调控教育部重点实验室(湖南师范大学)开放课题基金(QSQC0908)和湖南科技大学科学研究基金(E50818)的资助.
[1]G.L.Long,Y.S.Li,W.L.Zhang and C.C.Tu,Dominant Gate Imperfection in Grover's Quantum Search Algorithm[J]Phys.Rev.2000.
[2]Haeberlen U,Wangh JS.Coherent Averaging Effeets in Magnctic Resonance[J].Phys.Rer.,1968,175:453-467.
[3]Zanardi P.Symmetrizing evolutions[J].Phy.Lett.A,1999,258(1):77-82.
[4]Viola L,Lloyd S,Knill E.Universal Control of Decoupled Quantum Systems[J].Phy.Rev.Lett.,1999.83:4888.
[5]Y.H.Wang and X.S.Liu and G.L.Long,General Decoherence Suppression in Three-Level Atom in V-and ΞConfiguration[J].Commu.Theor.Phys.2008,49(4):881-886.
[6]Y.H.Wang and X.S.Liu and G.L.Long,Suppression of Phase and Amplitude Damping in a Three-Level Atom inλ-Configuration Using Bang-Bang Controls[J].Commu.Theor.Phys.2008,48(1):71-74.
[7]Y.H.Wang and X.S.Liu and G.L.Long,Suppression of Amplitude Decoherencein Arbitrary n-Level Atom in Configuration with BangBang Controls[J].Commu.Theor.Phys.,2008,49(6):1432-1434.
[8]Y.H.Wang,Liang Hao,Xiang Zhou and G.L.Long,Behavior of Quantum Coherence of-type four level atom zvnder BangBang Control[J].Opt.Commu.2008,281:4793-4799.

