基于端元提取的超光谱图像目标检测算法
张文希, 郑 茂, 李 纲
(1.长沙学院电子与通信工程系,长沙 410003;2.国防科学技术大学电子科学与工程学院,长沙 410073)
0 引言
超光谱遥感是从20世纪80年代发展起来的一项新型遥感技术,已经成为遥感技术的前沿科技。超光谱遥感是指利用很多很窄的电磁波波段从感兴趣的物体中获取有关数据,将确定物质或地物性质的光谱与把握其空间与几何关系的图像结合在一起[1],所获取的地表图像涵盖了丰富的空间、辐射以及光谱信息,较高的光谱分辨率使得超光谱数据能够探测到具有诊断性光谱吸收特征的物质,在国民经济的各个方面得到了广泛的应用。
超光谱图像的目标探测已经成为超光谱遥感最为重要的应用方向之一。在超光谱图像目标检测领域,目标检测可以通过空间的、光谱的或者两者相结合的方式来进行。在已知目标光谱的条件下,正交子空间投影(Orthogonal Subspace Projection,OSP)技术可以获得超光谱图像中的目标分布情况[2]。RX(Reed-Xiaoli)检测算子能够有效检测出图像中的异常信息,是超光谱图像中的经典检测算子,但该算子的检测结果更倾向于图像中的异常信号[3]。李庆波等提出了基于光谱奇异值检测的高光谱图像小目标检测算法,获得了较好的小目标探测准确度[4]。J.C.Harsanyi博士提出了约束能量最小化(Constrained Energy Minimum,CEM)算子,它不需要图像的背景信息,仅仅知道目标光谱即可[5]。寻丽娜提出了一种基于CEM的超光谱图像小目标检测算法,该算法首先对原始图像进行背景信息抑制从而抑制背景地物、突出低概率的小目标,用迭代误差分析的自动端元提取算法找出目标的端元光谱,然后把目标端元光谱代入CEM滤波器得到该目标的检测结果[6]。本文提出了一种超光谱图像目标检测算法。首先利用基于噪声调节的主成分分析(NAPCA)对原始数据进行变换,然后利用无监督的端元提取方案获得端元矢量,将其代入改进的CEM检测算子,实现了超光谱图像目标的有效检测,实验结果验证了算法的有效性。
1CEM及其改进算子
CEM算子利用特定的约束条件来设计一个有限脉冲响应滤波器,该滤波器能够让感兴趣的目标通过,同时,抑制了由其他信号带来的滤波器输出能量。假定{r1,r2,…,rN}为超光谱图像的像元矢量,N为总的矢量数,d为感兴趣的目标端元矢量,CEM算子的表达式为[5]

其中:R为原始数据的自相关阵,其表达式为
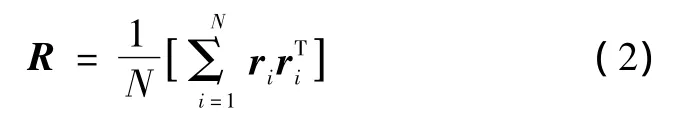
将w*作用于图像中的每一个像元矢量,得到感兴趣目标d在图像中的分布情况,实现对目标d的检测,即:
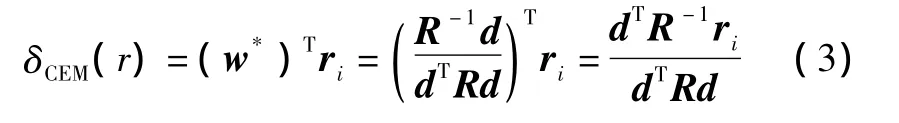
CEM算子对小目标探测具有很好的效果,但对于大目标,CEM算子的探测效果不佳,这主要是由于目标d既作为目标参与运算,同时也作为背景的一部分进行运算,当感兴趣目标在图像中分布较多时,目标d会对背景信号的能量产生较大的影响。耿修瑞博士提出了基于加权样本自相关阵的目标检测方法[7],通过利用加权样本自相关阵代替原始的自相关阵,极大改善了CEM对大目标的探测效果,其中加权自相关阵R*的表达式为

其中:f(0)=0;f(x)为单调递增函数(x≥0);c为常数;g(x,y)用于度量矢量x和y的相似度,它的取值随x和y相似度的增加而减小。将加权自相关阵用于计算CEM算子,可以得到基于加权样本自相关阵的探测算子,其表达式为

作者给出了3种加权方式,本文采用基于光谱角加权的自相关矩阵。
2 基于改进的CEM算子的目标探测算法
在改进的CEM算子基础上,本文提出了一种超光谱图像小目标探测算法,如图1所示。该算法首先对超光谱图像进行几何端元提取,获取图像中的目标端元矢量,然后再对原始数据进行NAPCA变换,保留部分信噪比较大的主成分;结合所提取的端元矢量,利用改进的CEM算子从保留的主成分中实施目标探测,从而得到最终的目标探测结果。

图1 本文提出的超光谱图像目标探测算法Fig.1 The proposed algorithm of target detection for hyperspectral image
2.1 几何端元提取
超光谱图像具有相对固定光谱的特征地物类型称为端元。在满足线性混合的条件下,图像中的每个像元都可以由其中的所有端元线性混合而成,因此超光谱图像的端元提取是理解超光谱图像,继而对数据进一步处理的前提条件[8]。在未知任何先验信息条件下,首先需要通过端元提取算法得到感兴趣或者疑似感兴趣的目标端元矢量,再对小目标进行检测和提取。文献[9]中提出了一种无监督的正交子空间投影(Unsupervised Orthogonal Subspace Projection,UOSP)技术,用来自动获取图像中的端元光谱,并进行混合像元的分解。本文引入该方法获取超光谱图像中的端元矢量,其端元提取步骤如下:
1)首先从超光谱图像中找到最大谱向矢量,记为e1,将其作为第1个端元矢量;
2)以U=e1作为子空间,作投影阵=I-UU#(其中 U#=(UTU)-1UT,I为单位阵),并将其作用到超光谱数据上,搜索最大谱向矢量对应的空间位置,将其作为第2个端元矢量e2;
3)令 U=[e1e2],作投影阵=I- UU#,将其作用到原始超光谱数据,与步骤2)类似,可以得到第3个端元矢量,记为 e3,令 U= [e1e2e3];
4)重复步骤3),直至获得所需的端元矢量为止。
2.2NAPCA 变换
主成分分析根据各个主成分的方差由大到小进行排序,其不足是方差较小的主成分可能具有较高的信噪比(Signal-Noise Ratio,SNR),而方差较大的主成分可能都是噪声,因此,方差并不能有效表示主成分中信号能量的大小,而将SNR作为准则对主成分进行排序更为合理。NAPCA能够根据SNR对主成分进行排序[10],利用NAPCA对超光谱图像进行变换后,不但可以更好地保持数据中信号的能量,降低图像中的噪声,而且可以极大地提高算法的运算效率。其基本步骤为首先估计图像中的噪声协方差矩阵Kn,然后求得白化矩阵F,即:

将F作用于原始数据的协方差矩阵K,得到噪声白化后的协方差矩阵:

对Σ进行特征值分解,即:

其中:G=(u1,u2,…,uL)为正交的特征向量矩阵,Λ =diag(λ1,λ2,…,λL)为特征值矩阵,且 λ1≥λ2≥…≥λL≥0,L为波段数。经过NAPCA变换后的谱向矢量为

其中:μ为均值向量。
3 实验结果
为验证算法的有效性,对印第安遥感实验区数据进行仿真实验,该数据包含220个波段,覆盖波长范围为0.4 ~2.5 μm,光谱分辨率为 10 nm,空间分辨率为17 m。其中每个波段大小为145×145,图2给出了该数据第20波段图像。

图2 印第安实验数据Fig.2 Indiana pines dataset
文献[11]指出,该数据中主要包括16种地物,因此,本文利用基于UOSP的端元提取算法提取出16个目标端元矢量,图3给出了端元3、9、13、14、15的端元光谱曲线。将获取的端元光谱看作感兴趣的目标矢量,对超光谱数据进行NAPCA变换,然后将端元光谱代入改进的CEM算子进行目标探测,图4给出了与图3所示端元对应的目标探测结果。可以看出,CEM的探测结果并不理想,探测结果中存在较多噪声,改进的CEM算子在探测效果上要优于CEM,但仍然受到噪声的影响;本文算法通过对原始数据进行NAPCA变换,有效地降低了图像中的噪声影响,其探测结果明显优于CEM及其改进算子的探测结果,从而验证了算法的有效性。

图3 端元光谱曲线Fig.3 Endmember spectral profile
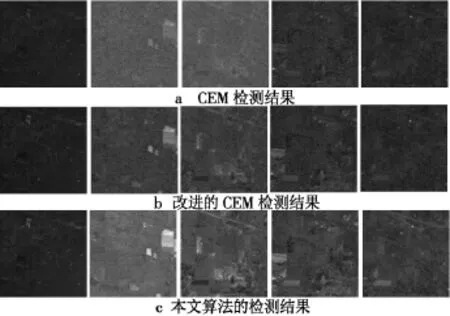
图4 目标检测结果比较Fig.4 Comparison of target detecting result
为验证算法在运算效率上的优势,对CEM算子、改进的CEM算子以及本文方法的运算时间进行了对比,如表1所示。CEM算子运算效率最高,但其探测效果不尽如人意;改进的CEM算子的运算复杂度较高,而本文方法在改进的CEM算子基础上,运算时间大大降低,并且探测效果也稍有提高。

表1 3种检测算法的运算复杂度比较Table 1 Complexity comparison of three algorithms
4 结论
超光谱图像小目标探测已经成为一个重要的应用方面。本文提出了一种超光谱图像小目标探测算法,首先引入NAPCA变换对原始数据进行处理,在获取图像中端元矢量的基础上,通过将端元矢量代入改进的CEM探测算子中,从而获得较好的目标检测结果,算法在运算效率上也具有一定的优势,在超光谱图像目标探测领域具有较好的应用前景。
[1]浦瑞良,宫鹏.高光谱遥感及其应用[M].北京:高等教育出版社,2000.
[2]HARSANYI J C,CHANG C I.Hyperspectral image classification and dimensionality reduction:an orthogonal subspace projection[J].IEEE Trans Geosci and Remote Sens,1994,32(4):779-785.
[3]STEIN D W J,BEAVEN S G,HOFF L E,et al.Anomaly detection from hyperspectral imagery[J].IEEE Signal Process Mag,2002,19(1):58-69.
[4]李庆波,李响,张广军.一种基于光谱奇异值检测的高光谱遥感小目标探测方法[J].光谱学与光谱分析,2008,28(8):1832-1836.
[5]HARSANYI J C.Detection and classification of subpixel spectral signatures in hyperspectral image sequences[D].University of Maryland,Baltimore County,1993.
[6]寻丽娜,方永华,李新.基于CEM的高光谱图像小目标检测算法[J].光电工程,2007,34(7):18-21.
[7]耿修瑞,赵永超.高光谱遥感图像小目标探测的基本原理[J].中国科学,2007,37(8):1081-1087.
[8]耿修瑞.高光谱图像异常探测与分类技术研究[D].北京:中国科学院遥感应用研究所,2005.
[9]吴波,张良培,李平湘.非监督正交子空间投影的高光谱混合像元自动分解[J].中国图像图形学报,2004,9(11):1392-1396.
[10]GREEN A A,BERMAN M,SWITZER P,et al.A transformation for ordering multispectral data in terms of image quality with implications for noise removal[J].IEEE Transactions on Geoscience and Remote Sensing,1988,26(1):65-74.
[11]LANDGREBE D.Multispectral data analysis:a signal theory perspective[D].Purdue University,1998.

