基于粒子滤波的扩展目标检测前跟踪算法

于洪波， 王国宏， 王 娜

(1.海军航空工程学院信息融合技术研究所，山东 烟台 264001;2.中国人民解放军92925部队，山西 长治 046011)

0 引言

传统的低分辨雷达中，目标被当作点目标进行处理，这是因为目标尺寸相对于雷达分辨单元来说太小，只能占据一个分辨单元［1］。对于高分辨雷达，目标将占据多个分辨单元，从而提供了目标更多的特征信息，这种目标被称为扩展目标［2］。这种情况下，在不同时刻雷达得到的目标回波是目标上不同扩展散射点发出的，如果把目标继续当作点目标来处理，就会漏掉许多特征信息，甚至会导致检测漏报和跟踪发散。

对于扩展目标，国外已进行了许多相关研究。文献［3］把一群点目标当作扩展目标进行处理，重点讨论了目标散射点服从泊松分布时目标跟踪情况;文献［4］提出了基于最大似然比的扩展目标跟踪算法，研究了目标发生旋转时的跟踪问题;文献［5］讨论了扩展目标散射点的空间分布情况，采用多假设卡尔曼滤波的方法实现扩展目标跟踪;文献［6］比较了点目标和扩展目标的异同点，并采用检测前跟踪的思想对扩展目标进行了跟踪检测。

以上文献研究了不同情况下扩展目标跟踪检测的问题，但是都没有对扩展目标空间长度作出有效的估计。针对这个问题，本文基于粒子滤波，对扩展目标进行检测前跟踪，并把目标强度和空间长度引入状态向量，以目标状态似然函数比［7－8］作为粒子权重从而估计目标状态，实现对扩展目标的有效跟踪检测。

1 算法描述

1.1 扩展目标运动模型

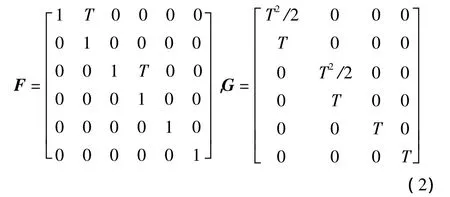
考虑一杆状目标在x-y平面内运动，定义目标的状态向量Xk=［xk，˙xk，yk，˙yk，Ik，Lk］T，Ik，Lk分别表示扩展目标的强度和空间长度，(xk，yk)，(˙xk，˙yk)分别是目标中心的位置、速度。系统状态方程描述为

其中:F为状态转移矩阵;G为过程噪声分布矩阵。

vk为零均值高斯白噪声，其协方差矩阵Q为

用Ek表示k时刻目标的存在状态，Ek={0，1}，0表示目标不存在，1表示目标存在。定义目标初始存在概率 μ0=P(E0=1)，目标出现概率Pb=P(Ek+1=1|Ek=0)，目标消失概率 Pd=P(Ek+1=0|Ek=1)，则Ek的状态转移矩阵表示为。

1.2 量测模型

为简明表述本算法，假设目标沿x轴运动，每一时刻目标上仅有一个散射点发出回波，散射点在目标上均匀分布，则散射点状态为

在时刻k传感器产生一组二维量测，这组量测是警戒区域内Nx×Ny个分辨单元的强度数据:Zk={z(i，j)k，i=1，2，…，Nx，j=1，2，…，Ny}，传感器分辨单元大小为Δx× Δy，k时刻分辨单元(i，j)的观测强度表示为

其中:h(i，j)k(χk)表示散射点 χk对分辨单元(i，j)的强度产生的影响，称作传感器点扩散函数，一般情况下h可近似为二维高斯概率密度形式［9］，则散射点χk在传感器分辨单元(i，j)的强度影响为

1.3 似然函数

k时刻，对于目标状态Xk，根据散射点状态模型，可得目标量测似然函数:

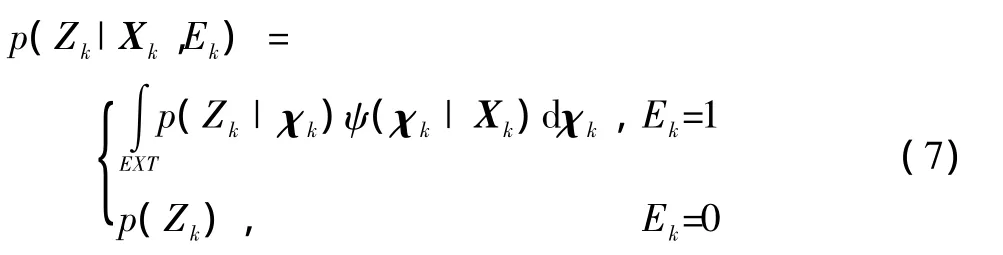
其中:p(Zk|χk)是k时刻散射点χk生成量测Zk的概率;ψ(χk|Xk)是目标状态为Xk时散射点χk的概率密度函数。基于随机采样的蒙特卡罗方法的核心思想是将积分运算转化为有限采样点的求和运算［10］，当Ek=1时，采用蒙特卡罗仿真方法，选取 M个采样点～ψ(χk|Xk)，则式(7)中第一部分可近似为

根据1.2节中传感器量测模型，结合式(7)、式(8)，传感器量测的似然函数可表示为

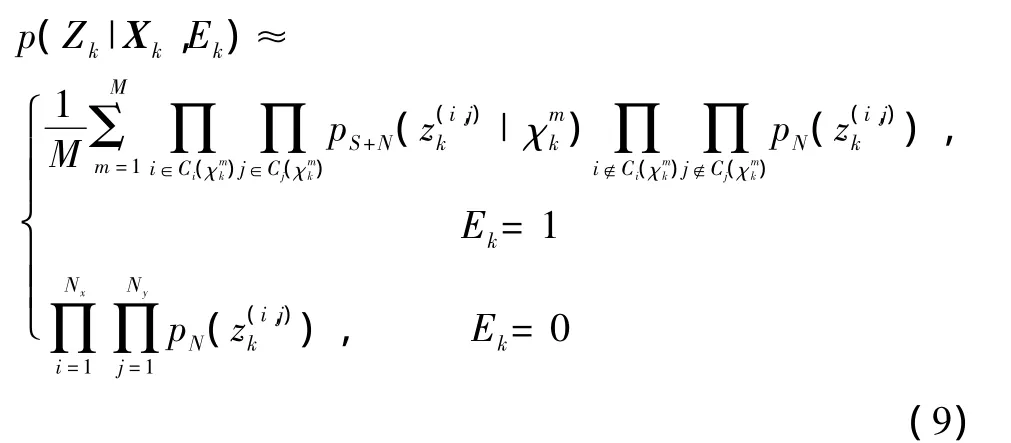
其中:pS+N()是目标状态为Xk时散射点加噪声在分辨单元(i，j)处的似然函数;pN()是背景噪声在分辨单元(i，j)处的概率密度函数;ci()，是受到散射点回波强度影响的分辨单元下标的集合。为简化说明，定义似然比:

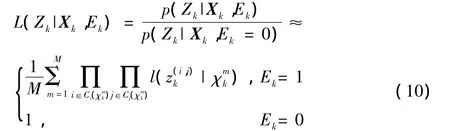
其中:

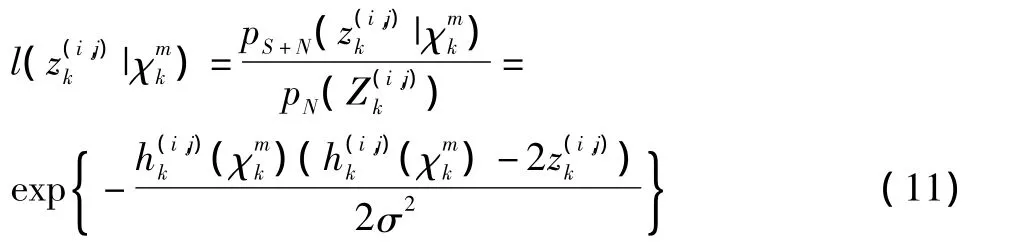
1.4 粒子滤波算法

粒子滤波(Particle Filter)是一种基于蒙特卡罗仿真的最优递推Bayes算法，其基本思想是根据一组带有相应权值的随机样本来近似表示目标的后验概率密度函数，并由此对目标的状态进行估计［11－12］。粒子滤波算法后验密度函数可表述为

粒子滤波算法的一个主要问题是退化问题。减少退化现象影响的方法一般有两种，一是选择比较好的重要密度函数，另一种是使用重采样技术。重采样方法基本思想是消减权值较小的粒子，集中权值较大的粒子［11］。本文中采用强制重采样的方法实现粒子滤波过程。设粒子数为N，算法实现具体过程如下:

1)k时刻，根据目标初始存在概率μ0和存在状态转移矩阵φ，预测粒子的存在状态{;

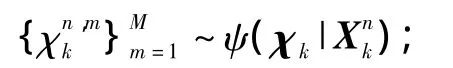
4)按照式(10)、式(11)，计算粒子权重并归一化:

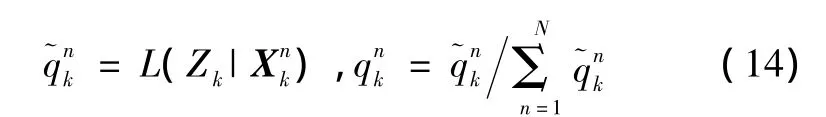
5)对粒子进行强制重采样，得到粒子更新:

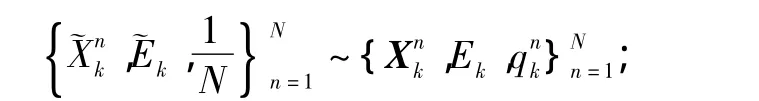
6)估计目标状态:

7)得到目标强度和空间长度的估计，实现目标检测。由目标状态形式Xk=［xk，，yk，Ik，Lk］T，结合6)得到目标强度和空间长度的估计:;目标存在状态的后验概率为，设定一个门限λ=0.6，当≥λ时，则认为检测到目标。

2 算法实验

2.1 仿真条件

为验证本文算法的有效性，进行了100次蒙特卡罗仿真。仿真环境为二维平面，传感器参数设置为Δx× Δy=0.7 ×0.7，Nx=20，Ny=10，Σ =0.7，目标归一化强度为I=20 Pu(Pu表示归一化强度单位)，目标空间长度为 L=0.3。

传感器观测噪声方差σz由背景噪声信噪比决定，本文采样文献［12］中信噪比定义方法:

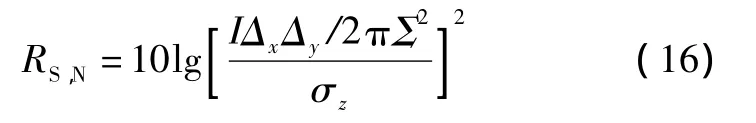
则信噪比为10 dB，6 dB 时，分别为1.006 6，1.595 3。

目标参数设置为:目标为匀速直线运动，雷达扫描周期为T=1 s，共仿真33个扫描周期。目标在第6个扫描周期出现，沿平行于x轴的方向匀速直线运动，一直持续到第31个扫描周期消失，目标初始状态为x0=(2.2，0.5，4.5，0，20，0.4)T，=0.001，=0.000 1，=0.01，=0.000 1。

粒子滤波参数设置为:粒子初始位置(x，y)在空间［0，14］× ［0，7］内均匀分布;粒子初始速度(x˙，y˙)在空间［－1，1］×［－0.1，0.1］内均匀分布;粒子初始强度服从均匀分布I～U［10，30］;粒子初始长度服从均匀分布 L ～ U［0.2，0.4］;粒子数为 N=2 000;粒子初始存在概率μ0=0.05;粒子存在状态的转移矩阵为φ=。

图1给出了信噪比为6 dB时第7个时刻的观测数据，观测以能量灰度图的形式给出，并把目标真实位置和能量散射点的位置做出了相应标示。图2给出了初始粒子的随机分布样本，为便于比较同时给出了时刻7时目标的真实状态，实心矩形表示真实目标，空心矩形表示粒子样本，矩形在X轴的宽度分别表示真实目标和粒子样本的扩展长度。

图1 观测数据图Fig.1 Simulated measurement data

图2 初始粒子随机分布样本Fig.2 Random distribution of initial particles

2.2 仿真结果与分析

采用以上实例来验证算法的有效性，图3和图4分别是信噪比为10 dB，6 dB时对目标进行仿真得到的目标跟踪和检测效果图。可以看出在10 dB时，目标检测性能很好，目标一出现就能立刻被检测到，同时跟踪精度很高;在信噪比为6 dB时，目标在第7个扫描周期出现，但直到第9个扫描周期才被检测到，需要积累3个扫描周期，同时只要检测到目标，就能有效跟踪目标，跟踪精度也很高。

图3 信噪比为10 dB时跟踪和检测效果图Fig.3 Tracking and detection performance with SNR of 10 dB

图4 信噪比为6 dB时跟踪和检测效果图Fig.4 Tracking and detection performance with SNR of 6 dB

图5和图6分别是信噪比为10 dB，6 dB时对目标强度和扩展长度特征进行估计得到的仿真效果图。

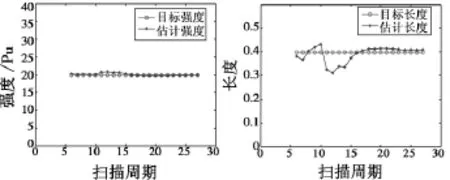
图5 信噪比为10 dB时目标的特征估计Fig.5 Estimation of target features with SNR of 10 dB

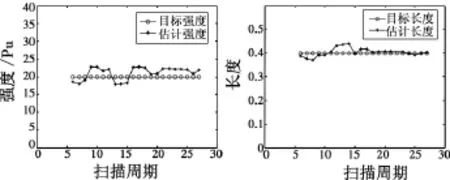
图6 信噪比为6 dB时目标的特征估计Fig.6 Estimation of target features with SNR of 6 dB

从结果中可以看出，该方法可以较好地估计目标的强度特征。在高信噪比时目标强度的估计精度较高，在低信噪比时目标强度的估计有一定起伏，但最终趋于平稳;对于目标长度的估计，两种信噪比下都能较好地得到目标长度估计值，信噪比提高时对估计精度影响不太明显，这是因为目标长度的估计精度主要取决于算法中对目标散射点分布情况的拟合程度，而与信噪比的关系不大。

3 结束语

本文提出了一种基于粒子滤波的扩展目标检测跟踪算法，通过把目标强度和扩展长度引入状态向量的方法实现扩展目标的跟踪检测，并有效地估计目标强度和扩展长度。仿真表明，该方法具有较好的跟踪检测性能，对目标强度和扩展长度估计精度较高。为提高目标扩展长度的估计精度，下一步工作将针对多散射点扩展目标进行研究。

［1］丁鹭飞，耿富录.雷达原理［M］.西安:西安电子科技大学出版社，2002.

［2］TORSTENSSON J，TRIEB M.Praticle filtering for track before detect application［D］.Linkoping:Linkoping University，Sweden，2005.

［3］GILHOLM K，GOOSILL S，MASKELL S，et al.Poisson models for extended target and group tracking［C］//SPIE，Signal and Data Processing of Small Targets，San Diego，CA，USA，2005，5913:59130R.

［4］TSOU Haiping，YAN T Y.The extended-image tracking technique based on the maximum likelihood estimation［R］.Jet Propulsion Laboratory California Institute of Technology，1999.

［5］GILHOLM K，SALMOND D.Spatial distribution model for tracking extended objects［J］.Radar Sonar and Navigation，2005，152(5):364-371.

［6］BOERS Y，DRIESSEN H，TORSTENSSON J，et al.A track before detect algorithm for tracking extended targets［J］.Radar Sonar and Navigation，2006，153(4):345-351.

［7］李晓波，王晟达，梁娟.ESM与雷达航迹关联的最大似然估计算法［J］.电光与控制，2007，14(1):46-47.

［8］TONISSEN S M，BAR-SHALOM Y.Maximum likelihood track-before-detect with fluctuating target amplitude［J］.IEEE Trans Aerospace and Electronic System，1998，34:796-809.

［9］WEN C Y，LEE C H.Point spread functions and their applications to forensic image restoration［J］.Forensic Science Journal，2002(1):15-26.

［10］梁晓龙，冯金富，杨啸天，等.基于集群智能粒子滤波的弹道导弹跟踪［J］.电光与控制，2009，16(7):31-32.

［11］何友，修建娟.雷达数据处理及应用［M］.北京:电子工业出版社，2005:48-49.

［12］龚亚信，杨宏文，胡卫东，等.基于粒子滤波的弱目标检测前跟踪算法［J］.系统工程与电子技术，2007(12):2143-2148.