基于FPGA的光谱探测实时数据处理系统研究

刘辉志， 张记龙，2， 李 晓， 王志斌

(1.中北大学仪器科学与动态测试教育部重点实验室，太原 030051;2.山西省光电信息与仪器工程技术研究中心，太原 030051)

0 引言

随着光谱技术的快速发展，光谱探测在战场侦察、大气污染物检测、毒气探测等研究领域中有着越来越重要的应用，其中普遍采用傅里叶变换光谱技术获取待测光谱信息［1－2］。傅里叶变换光谱技术是通过把干涉条纹的图像信息转换成离散的数字量，然后再进行傅里叶变换从而得到相应的光谱信息。因此，光电转换是傅里叶变换光谱技术的重要环节，数字信号处理方法是得到光谱信息的必需手段。光谱信号的数字化和后期数字信号处理在整个光谱探测系统中占有重要地位。光谱信号采集的好坏直接影响到最终的光谱分辨率，光谱的探测时间主要由数字信号处理系统决定［3］。目前实现傅里叶变换主要有软件和硬件两种方法，由于用软件进行傅里叶变换受到指令周期本身的限制，延时长、速度慢，不能满足战场侦察、大气污染物检测、毒气探测等光谱获取的实时性需要，因此为提高光谱信息获取速度，研究FPGA硬件实时数据处理方法具有重要意义［4－5］。

1 系统设计

1.1 光谱探测系统结构

实时光谱探测系统主要分光路和电路两部分组成，在实时探测中，为获取待测光谱信息，建立了M-Z光学干涉装置，原理框图如图1所示。图中利用M-Z干涉具对入射光源信号进行分束后干涉，由聚焦透镜将干涉具出射的平行光束聚焦在线阵CCD探测器感光单元上，形成明暗相间的干涉条纹［6］。每个感光单元上的亮度被采样和量化，变换为随时间变化的周期性电压信号，经电平转换后，将这些时间序列电信号输入FPGA进行FFT处理，输出的实部虚部数据进行平方根求模运算，得到光谱信息。系统把最后的光谱信息通过串口传输到PC机，从而实时显示探测结果。

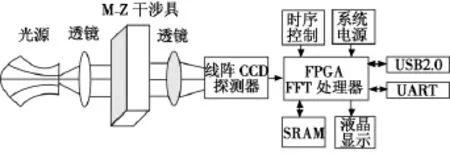
图1 实时光谱探测系统原理框图Fig.1 Principle of a real-time spectrum detection system

1.2 系统设计原理

入射光源经M-Z干涉具分束镜分束后，形成两束光，假设两束光的空间传递系数相同，设光强都为I0。这两束光频率相同、相位差一定、振动方向相同，因此满足干涉条件，在线阵CCD相机上可以得到光源的干涉条纹。两束光的振幅表示如下:

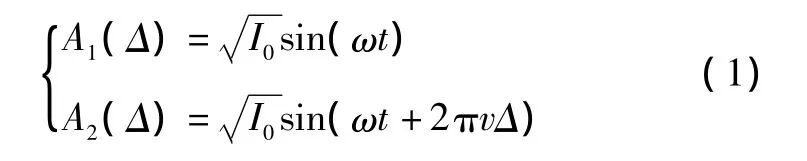
其中:Δ为光程差;2πvΔ为相位差;v为入射光源频率;ω为入射角与横切轴的夹角。干涉光的振幅可表示为

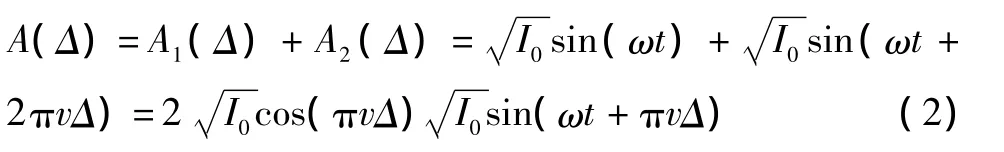
则干涉后的光强为

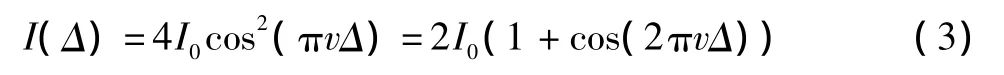
由于只有交流部分含有有效的光谱信息，干涉图背景成分，即直流部分不包含任何信息，可忽略不计。由于存在非理想因素故加入校正因子，若每条光束的光谱分布为I0(v)，则光束经过M-Z干涉具后输出的干涉强度为

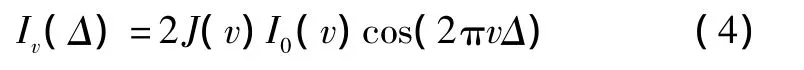
令E(v)=2J(v)I0(v)，则上式变为

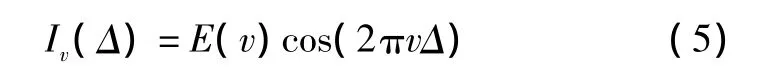
由于干涉信号为各频率成分干涉信号的叠加，因此在连续光入射时，干涉结果呈现积分效应:

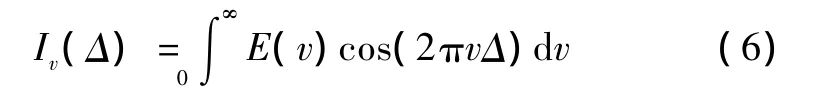
式中:Iv(Δ)为干涉强度随光程差变化的函数;E(v)为光谱强度随波数变换的分布函数。

从上式可见干涉图与光谱图之间有着傅里叶变换的关系，因此通过计算Iv(Δ)的傅里叶变换可从干涉图中得到目标的光谱分布E(v):

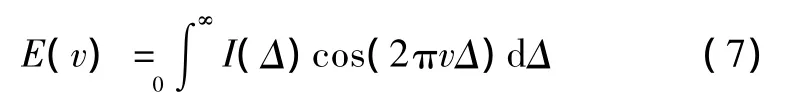
这就是傅里叶变换光谱原理。采集得到的干涉条纹数据经过整理，将线阵探测器像元序号的横坐标看成时间，进行快速傅里叶变换处理就可得到入射光的频谱分布［7］。

1.3 干涉条纹数据整理和切趾

根据傅里叶变换光谱理论，在进行傅里叶变换之前，由于直流部分为干涉图背景成分，不包含任何信息，应首先去除干涉图直流成分。对于等间隔离散干涉图可以采用下式，求出直流分量I:

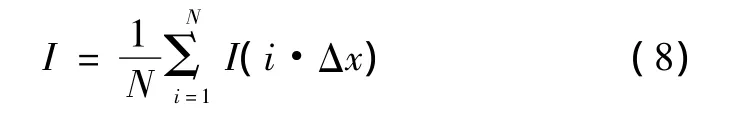
式中:N为数据采样点数;Δx为采样间隔。

然后利用下式去除干涉条纹的直流分量，获得相对于横坐标轴变化的干涉图:

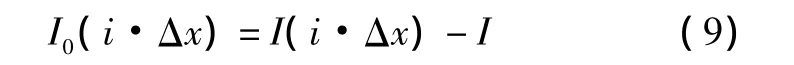
通常情况下，快速傅里叶变换对计算的数据要求为2n个，当采集获得的干涉条纹数据不能满足这一条件，可以对干涉条纹进行截取或添加零至2n个。数据添加零不影响光谱探测精度［8］。

经过以上数据处理后，获得了有限光程差范围区间上的干涉条纹，意味着强制干涉条纹函数在此范围之外骤降为零，导致干涉条纹在区间边缘出现尖锐的不连续性。计算还原后的谱线有“旁瓣”产生。旁瓣的产生会严重影响临近谱线，尤其是较弱谱线的准确测量，需要利用切趾法来缓和边缘不连续性，即一渐变权重函数(切趾函数)与干涉条纹函数相乘，起到一种空间频率滤波的作用，保证了强线附近的较弱光谱线测量［9］。

2 FFT硬件电路设计与仿真

2.1 FPGA 芯片

根据CCD探测器的像元数个数和精度，本文确定FPGA进行FFT数据处理的点数为1 024点，从实时处理和节省FPGA芯片逻辑资源压缩成本考虑，系统采用流水线基2-FFT算法处理。综上特点，系统选用的FPGA板卡为Xilinx公司Virtex2-Pro。该板卡主芯片XC2VP30，支持CameraLink接口标准，可以与CCD探测器接口直接对接，其资源情况如下:有30 816逻辑单元，136个18位的乘法器，2 448 kb的Block RAM和两个PowerPC。

2.2 1 024点基2-FFT模块设计

系统采用Xilinx公司软件开发平台ISE10.1，利用IP核设计了1024点流水线基2-FFT算法模块，比利用硬件描述语言编写的处理模块更加方便，逻辑综合生成模块如图2所示。

图2 FPGA设计生成的FFT模块Fig.2 FFT module designed by FPGA

2.3 1 024点基2-FFT功能仿真

利用VerilogHDL语言编写Testbench测试程序，在Modelsim6.3f仿真软件对模块进行功能仿真。芯片时钟频率为100 MHz时，系统复位后，当rfd为高电平时数据开始进入存储系统;在约5.2 μs时，busy为高电平，开始从存储系统中读取数据送入蝶形单元，进行运算;在约21.6 μs时，dv变为高电平，蝶形运算完毕，同时输出第一点FFT数据，直到done变为高电平时，1 024点FFT数据全部输完，系统共耗时约32 μs，波形仿真结果如图3所示。

图3 Modelsim6.3f仿真1 024点基2-FFT时序波形Fig.3 Time sequence simulation wave of 1 024-point radix 2-FFT by Mdoelsim6.3f

系统消耗FPGA芯片XC2VP30硬件资源如表1所示。

表1 实现1 024点基2-FFT消耗XC2VP30硬件资源Table 1 XC2VP30 resource consumption in implementation of 1 024-point radix 2-FFT

3 实验结果与谱线标定

3.1 实验结果

为验证数据处理系统1 024点基2-FFT模块实际计算结果是否正确，在实验室里进行了验证实验。实验中采用波长635 nm激光器照射干涉具，在CCD探测器上形成干涉条纹，把经过处理后的干涉条纹数据经过Matlab7.4进行二维图形分析如图4所示。理论计算该干涉条纹的1 024点基2-FFT频谱分布信息如图5所示。从图中可以看出，理论峰值点坐标分别为(117，50.75)，(909，50.75)，其横坐标代表干涉条纹个数，纵坐标代表能量，两峰值点是对称关系。

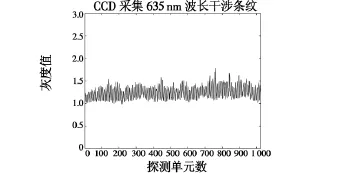
图4 CCD采集635 nm波长干涉条纹Fig.4 The interference fringe of 635 nm wavelength collected by CCD

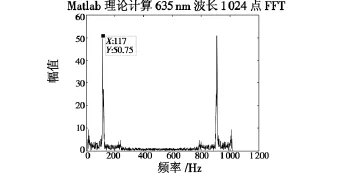
图5 Matlab理论计算635 nm的频谱分布图Figu.5 Spectrum distribution of 635 nm wave calculated by Matlab theoretically

根据1.3节中干涉条纹数切趾理论，FPGA实际计算干涉条纹的频谱结果，将前面几点和最后几点数据以零处理，通过Modelsim6.3f仿真后的数据导入Matlab7.4进行图形分析，得到其频谱分布信息如图6所示。

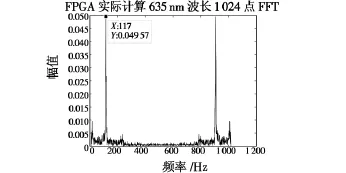
图6 FPGA实际计算635 nm的频谱分布图Fig.6 Spectrum distribution of 635 nm wave calculated by FPGA

从图6中可以看出FPGA实际计算干涉条纹的FFT 峰 值 点 坐 标 分 别 为 (117，0.049 57)，(909，0.049 57)，与Matlab理论计算的横坐标完全一致。理论幅值即能量是FPGA实际计算的1 024倍，这是由1 024点FFT算法系数造成的结果，具体计算时乘上系数即可。

3.2 谱线标定

图6中得到的是干涉条纹快速傅里叶变换后的空间频谱分布信息，它反映了产生干涉条纹光源的频率分布，如果光谱探测中要实时获取光源的波长分布信息，则还需要对干涉条纹的空间频谱分布信息进行转换，即谱线标定［10］。理论上，需要对干涉具所有波段的光都进行标定，但实际中，只能在某一光谱范围内，用尽可能多的不同波长的单色光进行有限个波长的标定，得到实际谱线与理论谱线的偏差，然后进行修正并重新标定。由于光路系统的干涉具固定不变，因此，在某一段范围内不同波长激光单位长度内的波数λ－1与该激光通过干涉具后单位长度内产生的干涉条纹的个数x的比值是常数c，即c=。如果在选取某一波长λ1作为基准后，根据干涉条纹数目就可以确定任意光源的波长由3.1节内容可知，635 nm激光形成的干涉条纹经过FPGA计算FFT后得出干涉条纹个数是117，易求得c值为134.59。

3.3 标定验证

为验证谱线标定的准确性，重新选用了波长850 nm激光器做实验，分别求得结果如下:CCD原始采集850 nm波长的干涉图如图7所示。

采用同样的处理方法，Matlab理论计算波长850 nm，干涉条纹1 024点FFT后频谱信息分布图见图8，其峰值点的坐标分别为(86，76.27)，(940，76.27)。FPGA实际计算波长850 nm干涉条纹1 024点FFT后的频谱分布信息如图9所示，其峰值点的坐标分别为(86，0.073 37)，(940，0.073 37)。

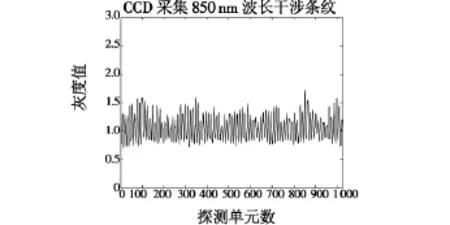
图7 CCD采集850 nm波长干涉条纹Fig.7 The interference fringe of 850 nm wave collected by CCD

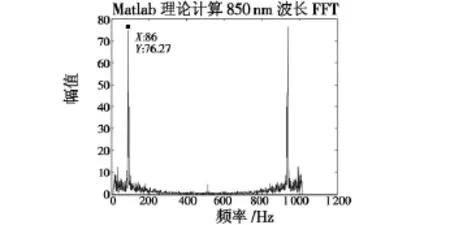
图8 Matlab理论计算850 nm的频谱分布图Fig.8 Spectrum distribution of 850 nm wave calculated by Matlab

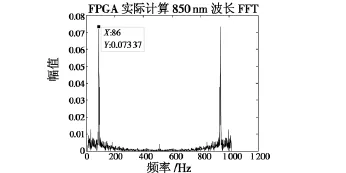
图9 FPGA实际计算850 nm的频谱分布图Fig.9 Spectrum distribution of 850 nm wave calculated by FPGA

由于系统干涉具不变，根据3.2节谱线标定原理，理论上两个不同波长分别与对应的干涉条纹个数的比值应该是相等的。经验证，当波长635 nm时，FPGA实际计算FFT后频谱分布信息图中干涉条纹数为117，计算得出c值为134.59;根据两组c值相等理论，可以求得当波长850 nm时，FPGA实现FFT后频谱分布信息图中干涉条纹数应该是87.41。但是，从上面验证实验中可以知道FPGA实际计算FFT后频谱分布中干涉条纹个数为86，与理论值87.41偏差1.41，相对误差1.6%。其中造成误差原因有干涉具加工精度、CCD探测器误差、以及人为测量误差等，后续可通过重复性测量和多次实验的方法减少误差。

4 结论

本文运用干涉条纹与光谱图存在傅里叶变换关系，利用高速FPGA芯片设计实时光谱探测系统数据处理模块，从实现结果看是行之有效的。当芯片工作频率在100 MHz时，完成线阵CCD探测器采集的1 024点基2-FFT数据处理约需32 μs，满足实时光谱探测的要求。并且系统具有体积小、运算速度快、稳定可靠等优点。实时光谱探测中数据处理系统的成功研制，将为战场侦察、大气污染物检测、毒气探测等实时应用领域提供良好的设计思路，对军民两用都有重要的现实意义。

［1］黄中华，王俊德.傅里叶变换红外光谱在大气遥感监测中的应用［J］.光谱学与光谱分析，2002，22(2):235-238.

［2］张记龙，聂宏斌，王志斌，等.化学战剂红外光谱遥测技术现状及发展趋势［J］.中北大学学报:自然科学版，2008，29(3):265-271.

［3］张敬波.基于DSP的傅里叶光谱仪测量控制系统［D］.长春:吉林大学，2004.

［4］王一程，汪海兵，赵长德，等.基于FPGA的光电跟踪控制系统设计［J］.电光与控制，2009，16(3):54-57.

［5］王远模，赵宏钟，张军，等.用FPGA实现浮点FFT处理器的研究［J］.国防科技大学学报，2004，26(6):61-64.

［6］张记龙，王志斌，李晓，等.光谱识别与相干识别激光告警接收机评述［J］.测试技术学报，2006，20(2):95-99.

［7］袁浩浩，张记龙，张联盟.激光光谱探测的FPGA实现［J］.微计算机信息，2009，25(1):214-215.

［8］李志刚.紫外真空紫外傅里叶变换光谱技术的研究［D］.长春:中科院长春光学精密机械与物理研究所，2000.

［9］殷世民，相里斌，周锦松.基于FPGA的干涉式成像光谱仪实时数据处理系统研究［J］.红外与毫米波，2007，26(4):274-278.

［10］薛尚峰.基于静态傅里叶变换干涉具的被动激光光谱探测技术研究［D］.太原:中北大学，2008.