大学化学中若干平衡问题的理解和思考

吴振玉 裘灵光 宋继梅 李村 朱维菊

(安徽大学化学化工学院 安徽合肥230039)

大学化学中若干平衡问题的理解和思考

吴振玉 裘灵光 宋继梅 李村 朱维菊

(安徽大学化学化工学院 安徽合肥230039)

在教学中，通过引导学生对一些平衡问题的基本概念进行深入思考和讨论，指导学生对有关数学问题进行严密推导和论证，既提高了学生解决实际问题的能力，又培养了学生严密的科学思维和严谨的科学态度。

在大学化学教学中，有关平衡问题的概念和理论涉及热力学平衡、酸碱平衡、沉淀溶解平衡、氧化还原平衡、配位平衡等问题。在教学中，引导学生对一些基本概念进行较为深入的思考和讨论，对其中涉及的一些数学问题，利用其实际物理和化学意义，根据需要对数学公式进行变通和化简，或对涉及的数学问题进行严格的推导和论证，以激发学生的学习兴趣。下面以缓冲溶液pH计算与质子平衡和化学平衡与自发变化为例进行简单介绍。

1 缓冲溶液pH计算与质子平衡

PBE(质子平衡式，proton balance equation)法是计算溶液氢离子浓度的基本依据，通过此法可以得到计算溶液中氢离子浓度的精确计算式，还可以根据一定的条件分别得到近似式和最简式。相关文献［1-6］虽然对PBE的变通写法和化简方法做了一些讨论，但是很少有直接利用PBE计算缓冲溶液pH的方法介绍。因此，我们在教学中引导学生在这方面进行了讨论和思考。以下以一元弱酸HA及其盐NaA(设其初始浓度分别为ca和cb，并设HA电离部分及A－水解部分的浓度分别为x和y)组成的缓冲体系为例，演示PBE的变通写法和直接利用PBE推导缓冲溶液pH计算的精确式、近似式和最简式的变通及化简方法。

首先，写出PBE，利用平衡常数关系找出PBE中各物种的表达式(为简便起见，公式推导中省略c⊖)。

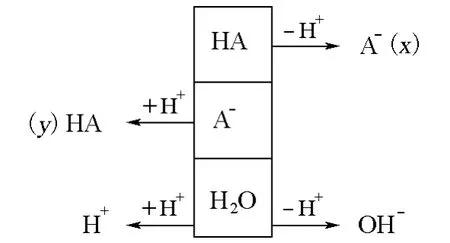
根据PBE的意义可知，该体系的质子平衡式如下:

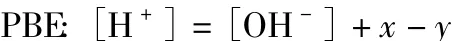
由HA的电离平衡和A－的水解平衡可知ca、cb与x和y的关系如下:

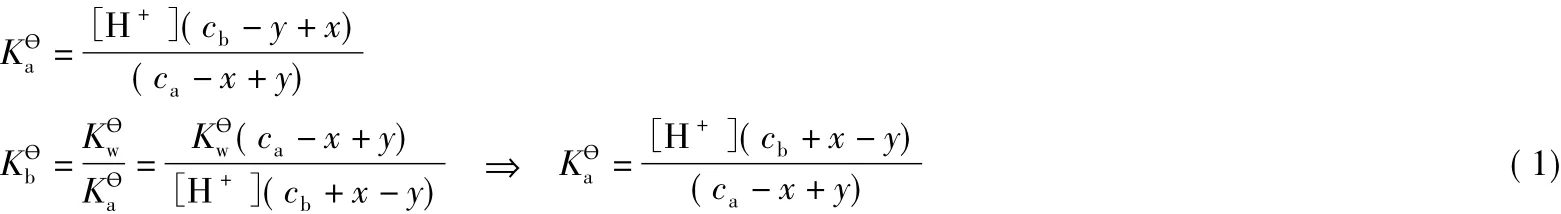
解(1)得:

把式(2)带入PBE中，得到缓冲溶液pH的精确式计算如下:

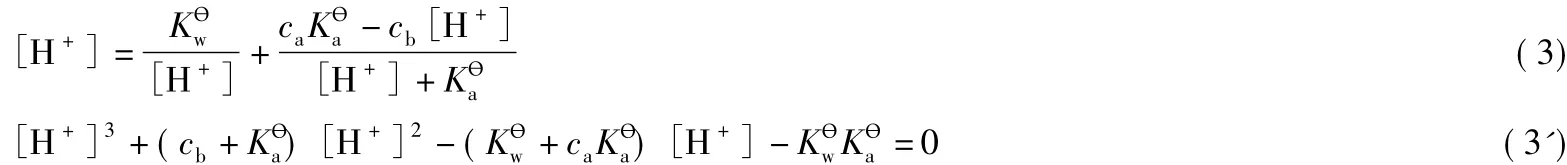
式(3)和式(3')即是缓冲溶液pH计算的精确式。

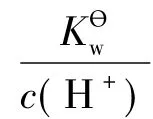
式(4)经整理后为:

当pH＞8时，忽略x(电离生成的H+很少，即对应的x也很小)，即式(1)和式(2)中去掉x，把去掉x后的式(2)带入PBE的表达式，结果仍然如式(3)。式(3)可整理为如下形式:

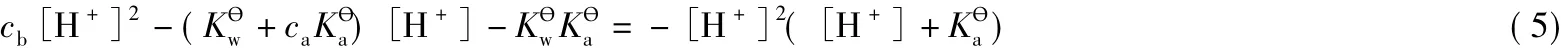
当pH＞8时，［H+］2(［H+］+)≈0，所以式(5)可变为:

式(6)即缓冲溶液pH的另一种近似计算式。把精确式(3')整理为如下形式:

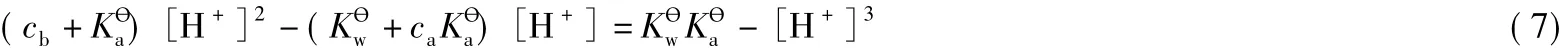
通常情况下，缓冲溶液pH不会太小，而且其ca或cb均较大，远远大于或，也比大得多，即把以上条件带入式(7)，得到缓冲溶液pH计算的最简式如下:

以上直接利用PBE推导所得缓冲溶液pH计算的精确式、近似式和最简式与文献［1］一致。通过以上推导引导学生理解和思考缓冲溶液pH计算的问题，不仅可以使学生更好地理解PBE的概念，明白缓冲溶液pH计算中精确式、近似式和最简式的关系，而且可以学会如何对具有实际物理和化学意义的数学公式进行变换，达到解决问题的目的。

2 化学平衡与自发变化

在大学化学教材中［6-10］，化学平衡与自发方向这一内容涉及许多基本概念。引导学生对相关概念进行归纳总结，区分其异同，可以准确地理解和掌握这些基本概念。

2.1 自发变化与系统(体系)

一般的大学化学教材［1，7］中，都是用类似“不需外力，任其自然，即可自动进行”的语言描述自发变化，并列举温度传递、浓度扩散、水往低处流、铁生锈等自发变化的实例。但是学生对如反应CaCO3(s)CaO(s)+CO2(g)高温自发的描述不容易理解，既然是高温，必定借助了外力进行加热，怎么又说是自发呢?针对上述问题引导学生从“体系(系统)与环境”这个热力学的基本概念出发，就能够更好地加深理解。上例中高温自发的前提是指我们选择的体系本身已处于高温，符合“不需外力，任其自然，即可自动进行”的自发变化条件，而不需要借助外力再进行加热或降温。可引导学生从本例讨论“体系(系统)”与“环境”的划分。

2.2 各种平衡常数

在确定化学势中各物质的标准态后，把反应系统中各物质的化学势代入系统的Gibbs自由能表达式中，并引入条件fB≈pB，ax，B≈xB，ac，B≈cB，am，B≈mB，可以推导出各种标准平衡常数(热力学平衡常数)。即:①纯气相反应中的标准平衡常数;② 溶液中反应的标准平衡常数、和;③固体溶液中的反应，其标准平衡常数与溶液中反应的热力学平衡常数类似。

应用注意:多相反应的标准平衡常数中，气体用相对分压p/p⊖表示，溶液中的溶质用相对浓度c/c⊖表示，因为对于纯态凝聚相aB=1，所以纯态凝聚相不出现在平衡常数表示式中。另外，还要注意标准平衡常数与Δr对应，经验(或实用)平衡常数Kp，Kc，Kx并不与Δr产生直接的联系，在应用计算中要考虑逸度系数及活度系数时，需要用以逸度或活度表示的平衡常数。

从以上思路引导学生对各种平衡常数进行归纳总结，有助于学生理解和记忆这些繁杂的概念。

2.3 Δr、ΔrGm与K⊖、Q(反应熵)

在学习化学反应等温方程式时，学生很容易混淆概念，把处于Δr时的反应系统与已经达到化学平衡时的反应系统等同起来。事实上，反应系统处于Δr时，Q=1;处于平衡时，Q =K⊖，ΔrGm=0。反应系统处于Δr时，其反应的自发方向取决于该反应的K⊖是大于1还是小于1;大于1则正向自发，小于1则逆向自发。例如酸碱平衡中的和，沉淀溶解平衡中的，配位平衡中的等远远小于1，因此处于Δr时的反应系统，朝着生成弱酸、弱碱、沉淀或配合物的方向自发进行。

2.4 K⊖与和

一般教材中都会讲到几种平衡常数的换算关系，特别是对于气相反应中的与，但是化学反应等温方程式中的K⊖通常并没有给出下标，以限定是标准压力平衡常数还是标准浓度平衡常数。因而学生经常会问:对气相反应而言化学反应等温方程式中的K⊖用或是否都可以?显然，对于同一个反应体系，除个别情况(反应前后气体分子数不变)下，和并不相等，而同一个反应体系的Δr是确定的，因此和不能随便使用。在教学中可以引导学生从标准平衡常数的导出来讨论这个问题，通过文献阅读和分析可知:由于推导不同标准平衡常数时，所用的各物质化学势中的标准态不同［6-10］，因而与不同标准平衡常数对应的ΔrG也不同。通常对气相反应取压力标准平衡常数及对应的(T)而得到Δr;溶液中的反应用浓度标准平衡常数;对复相(或多相)反应，气体和溶质则分别取相对分压力、相对浓度以及对应的(T)，而得到Δr，所以对复相(或多相)反应，K⊖不指明是标准压力平衡常数还是标准浓度平衡常数。总之，对气相反应而言，一般用，如果用带入等温方程式，则需要乘一个相应的换算系数。

2.5 为什么化学反应通常不能进行到底

在等温等压下，当反应物化学势的总和大于产物化学势的总和时，为什么化学反应通常不能进行到底?为了解答这一问题，教材［7］中以理想气体混合物的反应D(g，T，p)+E(g，T，p)2F(g，T，p)为例，做了简单推导。教学中为了培养学生严密的科学思维和严谨的科学态度，引导学生利用学习过的微积分知识对该例进行严格的数学证明，以严格的数学语言回答化学反应通常不能进行到底的原因，具体证明如下:

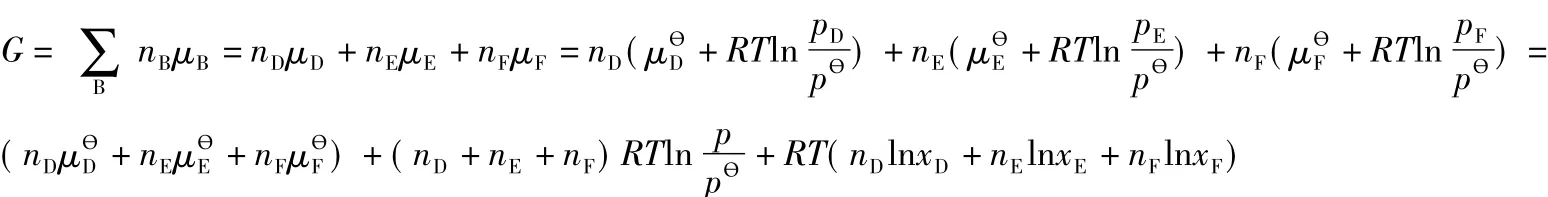
设反应从D，E开始，且其物质的量各为1mol，则在任何时刻，有:

从上式消去nE，nF，得:

令:

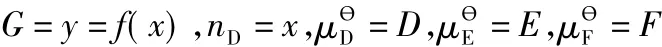
得:

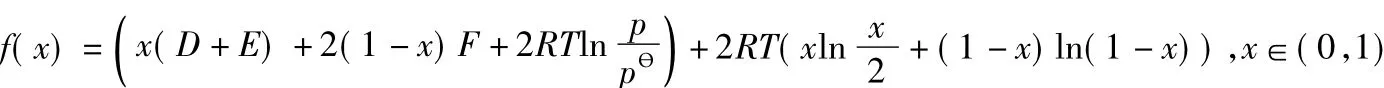
则:

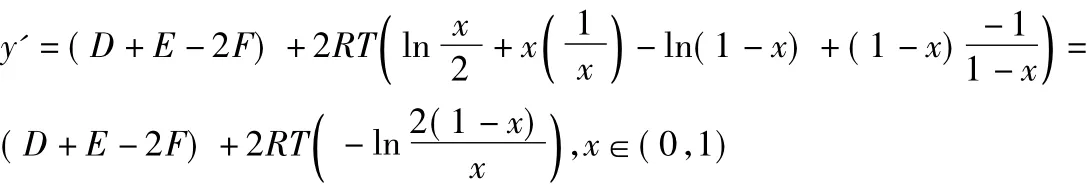
令:

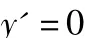
则:

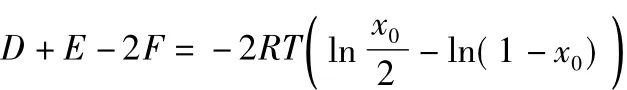
得:

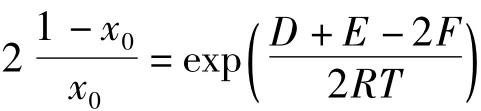
令:

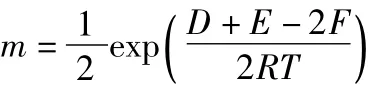
则:

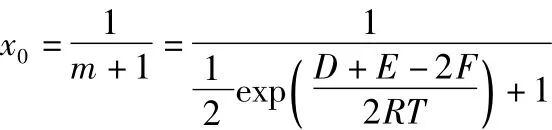
从反应的实际意义可知:D＞0，E＞0，F＞0，R＞0，T＞0;且均为有界的正数。所以:

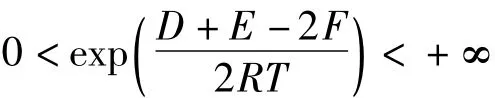
可得:x0∈(0，1)。

因为:

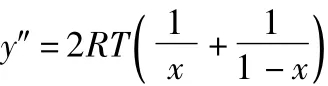
所以:

根据数学定理可知:x=x0为G=y=f(x)在x∈(0，1)上唯一的极小值点，即:G=y=f(x)在x∈(0，1)上有最小值。

由实际化学反应的意义可知:G=y=f(x)在x=0和x=1处的定义为:

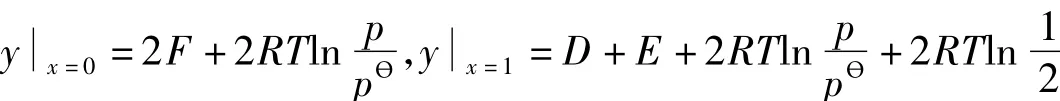
且:yx=1＞yx=0。

综上所述，可以得到G=y=f(x)的图像(图1)。

在本例中，反应进程ξ等于1－x，所以图1就是文献［7］中图6.1及图6.2 PTS曲线的严格数学证明。

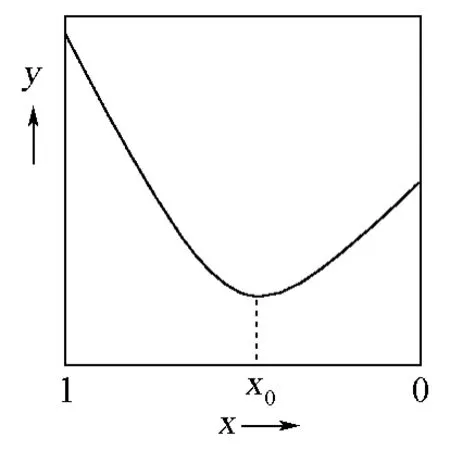
图1 G=y=f(x)的函数图像

［1］ 武汉大学.分析化学.第3版.北京:高等教育出版社，1995

［2］ 寇兴明.四川师范大学学报(自然科学版)，1998，21(2):238

［3］ 雷良萍.大学化学，1988，3(1):55

［4］ 章旭坤.化学通报，1988，51(2):43

［5］ 陈玲然，张懋森.丽水师范专科学校学报，1987，9(S2):62

［6］ 浙江大学.无机及分析化学.第2版.北京:高等教育出版社，2008

［7］ 傅献彩，沈文霞，姚天扬，等.物理化学(上).第5版.北京:高等教育出版社，2005

［8］ 黄子卿.物理化学.北京:高等教育出版社，1955

［9］ Atkins P，de Paula J.Atkins物理化学.第7版.影印版.北京:高等教育出版社，2006

［10］ 北京师范大学无机化学教研室.无机化学.第4版.北京:高等教育出版社，2002