利用循环法导出克拉贝龙方程*

陈良坦蒋新征

(1厦门大学化学化工学院 福建厦门361005;2福建省南安第一中学 福建南安362300)

利用循环法导出克拉贝龙方程*

陈良坦1蒋新征2

(1厦门大学化学化工学院 福建厦门361005;2福建省南安第一中学 福建南安362300)

提出一种基于可逆循环的克拉贝龙方程导出法。这种方法无须具备有关化学势的知识;并可使学生从另一方面熟悉循环法的应用，便于进一步加深对熵函数物理意义的理解。

作为描述单组分两相平衡的解析方法，克拉贝龙方程在处理诸如蒸气压随温度变化，凝固点随压力变化以及绘制单组分两相平衡边界线等方面有着实际应用。目前，有关克拉贝龙方程的导出方法主要有两种:一是物理化学教科书中普遍采用的以相平衡时两相化学势相等作为出发点并结合微元法进行方程推导的方法［1］，该方法简单、易懂，但必须掌握化学势知识;二是物理教科书(热学)中采用的由克拉贝龙在1834年利用一个可逆卡诺循环导出的方法［2］，该方法虽然简单，无须借助化学势的知识，但也有推导过程不够严谨，必须借助热机效率的结果等不足之处。本着启发学生思考问题、发现问题、提出问题之目的，笔者在此提出另一种利用含有相变的可逆循环而导出克拉贝龙方程的方法。

1 基本原理

设有一可逆循环，它由两步可逆相变过程和两步等容可逆过程组成(图1)。下面利用该可逆循环分别从焓变和熵变入手导出克拉贝龙方程。

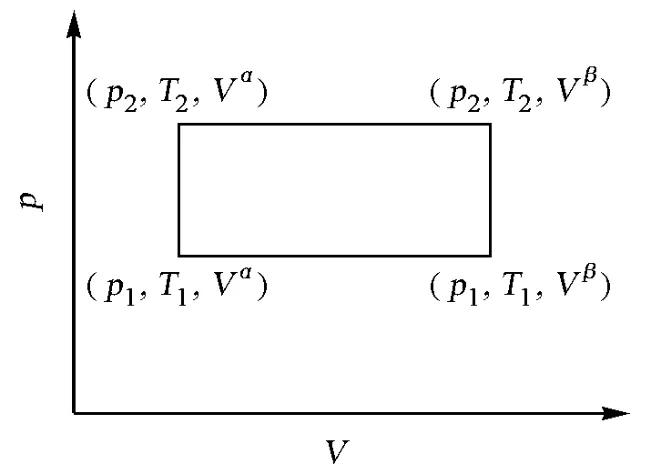
图1 含有相变的可逆循环

1.1 公式推导一

对此可逆循环，ΔU=0。故有:

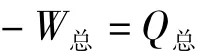
因循环中两步等容过程没有体积功，W2=W4=0。因此有:

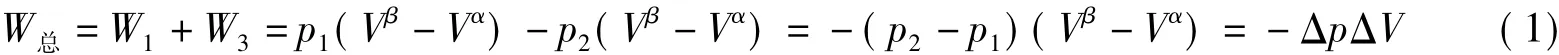
在整个循环中，两步可逆相变过程的热效应等于过程的相变焓，即:

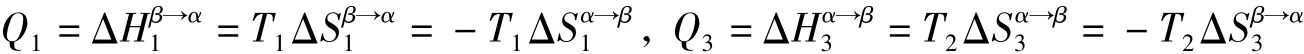
而循环中两步等容过程的热为:

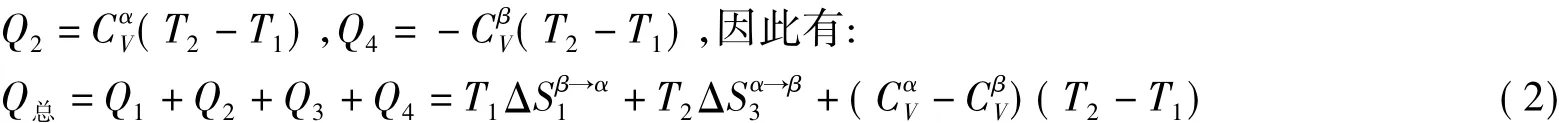
对此循环有:

当(T2－T1)→0，则有:

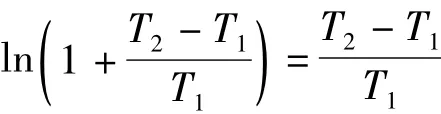
将其代入式(3)，得:

现设有物质的量为n的物质从α相转变到β相，则相变过程中其体积改变量及其与热源的热交换分别为:

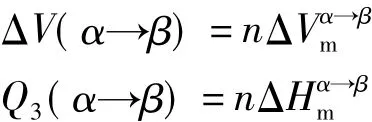
因此有:

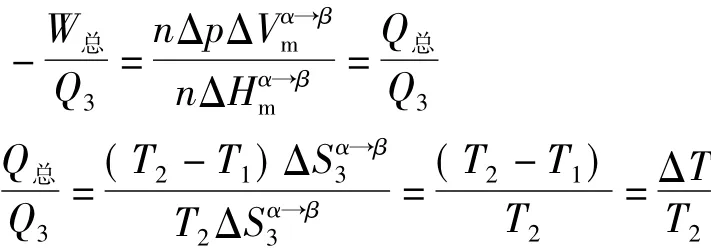
令Δp=d p，ΔT=d T，T2=T，整理得:

1.2 公式推导二

数学上可证明，对任意可逆循环，其热温熵之和必为0。因此，对上述循环，有:

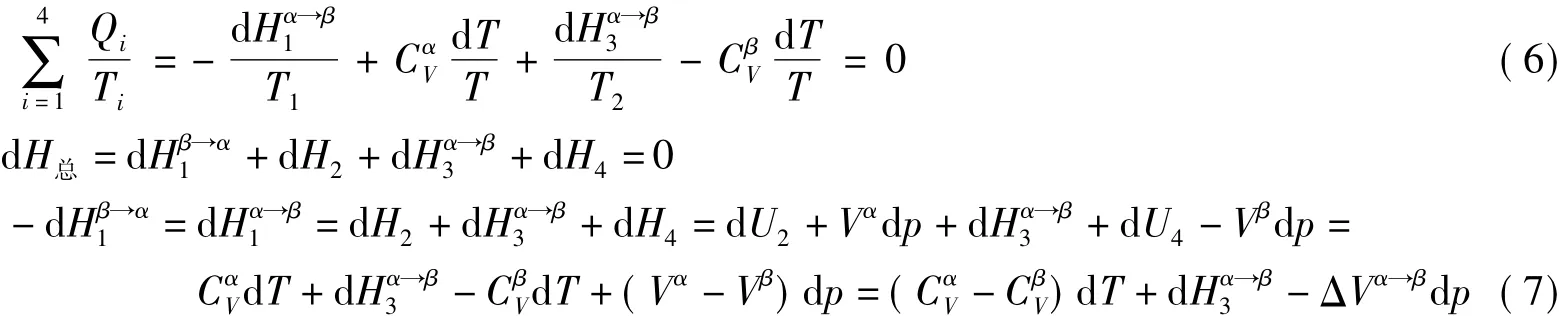
将式(7)代入式(6)可得:

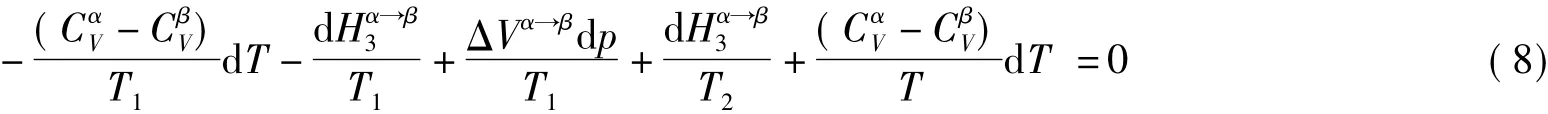
式(8)中

2 讨论

1)以基于可逆相变的循环为基础，导出了克拉贝龙方程，推导过程中并未作任何假设，是一个适用于任何单组分两相平衡的方程。由于推导过程无须掌握化学势知识，因此，这一方法也适合在讲授热力学第一定律(公式推导二)和热力学第二定律(公式推导一)时介绍。

2)与克拉贝龙1834年的推导方法相比，上述推导过程更为严格，无须借助热机效率的结果，这对于培养学生严谨的科学态度是有益的。

3)本方法所设计的可逆循环模型与一般教科书中介绍的卡诺可逆循环模型并不相同，鉴于学生对可逆相变过程更易接受，因此，对于启发学生从多个角度考虑问题也很有帮助。

4)通过公式的推导过程，可进一步帮助学生加深对过程熵变定义的理解。同时，公式的推导也可作为可逆循环热温熵之和为0的一种反证法［3］。

［1］ 韩德刚，高执棣，高盘良.物理化学.北京:高等教育出版社，2001

［2］ 赵凯华.新概念物理教程.热学.北京:高等教育出版社，2002

［3］ 陈良坦.大学化学，2008，23(1):63

厦门大学化学基地基金资助项目(J0630429)