股权违约互换定价
欧阳异能,王继红
(石河子大学 师院兵团教院,新疆 石河子, 832003)
股权违约互换定价
欧阳异能,王继红
(石河子大学 师院兵团教院,新疆 石河子, 832003)
讨论股权违约互换的定价问题. 假定标的股票价格服从几何布朗运动,当股票价格低于某一特定值时违约发生,在风险中性条件下利用无套利原理得到定价模型,采用拉普拉斯逆变换求得违约时间概率密度以及概率分布,最终给出股权违约互换价格.
股权违约互换;拉普拉斯逆变换;Girsanov定理;违约概率密度
股权违约互换(equity default swap,EDS)是一种新型信用衍生产品,自从2004年在欧美市场首发以来受到广泛关注,其交易规模也得到迅速发展. EDS是指买卖双方以第三方发行的股票为标的资产所达成的一种合约,买方有义务定期向卖方按比例(股权违约互换价格)支付费用,直到标的资产发生违约或合约到期(若无违约发生);而在合约期限内如果标的资产发生了指定的违约事件(通常是指价格下降为合约开始时的30%以下),此时卖方必须向买方支付违约损失. EDS期限一般为5年,每半年支付一次.
对于EDS的定价,目前主要是采用结构化方法,Albanese[1]认为信用质量下降直接导致违约事件发生,从而建立定价EDS的信用障碍模型. Medova[2]假设导致违约的唯一因素是公司资产价值的变化,给出了一个EDS定价结构化模型. 本文假定标的股票价格服从几何布朗运动,当股价低于某一特定值时违约发生,在风险中性条件下利用无套利原理得到定价模型,采用拉普拉斯逆变换求得违约时间概率密度以及概率分布,最终给出股权违约互换价格.
1 模型建立
假设金融市场概率空间为(Ω, F, P),P为市场概率测度,无风险利率为r. 标的股票价格服从(Ω, F, P)上的几何布朗运动dSt/St=μd t+σd Bt,μ, σ为常数,Bt为(Ω, F, P)上标准布朗运动. 假设合约签订时刻为零时刻,则初始股票价格为S0. 约定标的股票价格St首次低于阈值K时违约发生,即违约时间τ=inf{t≥0,St=K<S0}.

2 违约时间概率分布函数的计算



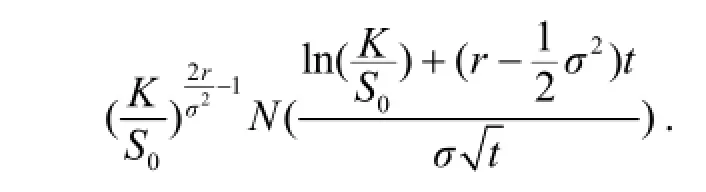
3 实例与小结

本文讨论了股权违约互换定价问题. 先根据无套利原理得出股权违约互换的定价计算方法,然后在风险中性条件下利用拉普拉斯逆变换求出了违约概率密度函数,并对模型进行了实例求解. 但本文只是在固定利率情形进行了建模,对于随机利率期限结构下的定价还需要进一步研究.
[1] Albanese C, Chen O. Pricing equity default swaps[J]. Risk, 2005, 18(6): 83-87.
[2] Medova E, Smith R. A structure approach to EDS pricing[J]. Risk, 2006, 19(4): 84-88.
[3] Manuel Ammann, 杨玉明. 信用风险评估——方法、模型、应用[M]. 北京: 清华大学出版社, 2004: 269-270.
[4] 钱敏平, 龚光鲁. 随机过程论[M]. 2版. 北京: 北京大学出版社, 1997: 317.
[5] 金忆丹. 复变函数与拉普拉斯变换[M]. 2版. 杭州: 浙江大学出版社, 1987.
The pricing of equity default swap
OUYANG Yi-neng , WANG Ji-hong
(Teacher College Bingtuan Education Institute of Shihezi University, Shihezi 832003, China)
The problem of pricing of equity default swap is discussed. Assume that the stock is modeled by a geometric Brownian motion, and define the default occurs when the stock price below a certain value, the pricing model is obtained by arbitrage-free principle under risk neutral measure, the probability density function of default time is obtained by Laplace adverse transform, then we obtain the pricing formula of equity default swap by the above results.
equity default swap; Laplace adverse transform; Girsanov theorem; default probability density
O 211.9;F 830.9
:A
1672-6146(2010)04-0014-03
10.3969/j.issn.1672-6146.2010.04.005
2010-09-26
欧阳异能(1979-), 男, 讲师, 硕士, 从事数理金融研究.

