三维陷落腔脉动压力分布特性实验研究
戴绍仕,姚熊亮,李 卓
(哈尔滨工程大学船舶工程学院,哈尔滨 150001)
三维陷落腔脉动压力分布特性实验研究
戴绍仕,姚熊亮,李 卓
(哈尔滨工程大学船舶工程学院,哈尔滨 150001)
文章针对均匀流场中三维深型陷落腔因流分离而产生的流激振荡问题开展了一系列的实验研究。在来流流速为0攻角时实验时的雷诺数变化范围:Re=1.55×105~8.74×105。实验中分别测量了三维深型陷落腔侧壁周向及垂向流体压力,分析了腔体内脉动压力周向、垂向的分布规律及腔口处剪切层自持振荡特性。实验结果表明:均匀流场中三维深型陷落腔内脉动压力分布较为复杂。在剪切层随边处的脉动压力最大,随边角点处脉动压力随相对高度的增加而陡降为0,但腔口导边及侧面处的脉动压力随相对高度增加而略有增大。剪切层自持振荡频率的无量纲数St数随Re变化为一常数值,但其值比气流场中二维陷落腔的St数略大。
深型陷落腔;均匀流;流激振荡;脉动压力;实验研究
1 引 言
陷落腔结构被广泛地应用在航天航空领域、航海领域、水利工程等领域中,如飞机起落架轮蓄井、船用海底阀箱及相关储液系统、槽形壁面的风洞和水洞等都属陷落腔结构。人们通常认为在三维陷落腔内的水是“死水”,即“死水”暗示着腔内流体的流速为0。但实际上当水流流过陷落腔时在腔口的导边处会发生流分离,然后因逆压的存在而产生涡体运动和剪切层自持振荡的现象。在剪切层振荡过程中将陷落腔内部水体与外部水体分开,使得腔内形成一循环水系,在此循环水系内有一大涡做低周运动,此时在腔体内部存在一种复杂的、垂向的、不稳定的三维流体运动。腔内较强脉动压力的变化可能诱发结构产生疲劳损伤或破坏。
到目前为止,有关二维陷落腔流激振荡问题的研究已取得了较为丰硕的成果[1-7],但多数研究主要集中在气流场作用下二维陷落腔剪切层自持振荡频率特性的验证与对比上,不仅忽略了腔内流体运动的三维效应而且不涉及腔体内部流体脉动压力的分布特性,而剪切层自持振荡作用会使陷落腔内部产生一种复杂的、垂向的三维流体运动。在这种情况下陷落腔内部的水动力问题还鲜有论文发表。
有鉴于此,本文在均匀流场中不同来流流速的情况下开展了三维深型陷落腔流激振荡问题的系列实验研究,给出了三维深型陷落腔内部脉动压力周向和垂向分布规律,以及剪切层的振荡特性,揭示了深型陷落腔内部流体运动机理,为三维深型陷落腔的疲劳计算提供参考依据。
2 实验模型与测量设备
实验在哈尔滨工程大学拖曳水池开展,拖曳水池长108m、宽7m和深3.5m,水池拖车最大速度可达6m/s,实验时水温为20°。实验载体—船模全长3.8m,宽1.0m和高0.8m,吃水0.4m、干弦0.3m,深型陷落腔的长×宽×高为 0.225×0.3×0.3,高跨比 H/L=1.333,见图 1,实验流速范围 0.6~3.39m/s,Δv=0.31m/s。在实验模型安装时为避免实验载体在实验中发生横摇、纵摇及不必要的振动而影响实验测试结果,本文在实验时将实验载体用80#槽钢与拖车前梁钢性连接,并在前梁与槽钢的连接处、槽钢与实验载体的连接处分别垫上厚为10mm的橡胶垫,见图2。为防止实验过程中腔体内存有空气,在三维陷落腔顶面中心设置φ30的排气管。

实验采用法国产的EPX-N12-0.7B/LTM/Z*微型压力传感器,采用LDS Nicollet多通道数据采集系统同时配有DH3842可编程应变放大器1台和电荷放大器1台,采样频率为0.5kHz,实验所测的稳定段时间不小于15s。
实验测量设备(压力传感器)分别布置在深型陷落腔腔口、垂向中截面及顶截面侧壁处,因深型陷落腔流体运动的对称性沿腔体周向仅布置一半压力传感器,为详细地观测腔口处剪切层振荡特性在腔口处布置了较多的压力传感器,传感器布置图如图3所示。

3 数据分析参数
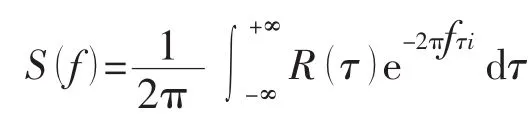

式中:ν为运动粘滞性系数,m2/s;V∞为流向速度,m/s;L为特征长度,本文取腔口在流向上的长度,m;fm为流体剪切层处自持振荡的各阶频率,Hz;ρ为实验状态下流体密度,kg/m3;p′(θ,t)为流体脉动压力均方根值,Pa。
4 实验结果分析
本文实验流速范围在0.6~3.39m/s,间隔为0.31m/s,共计10种流速。由腔体内三层侧壁脉动压力分布结果可以明显地看出在深型陷落腔体内存在复杂的流体运动,为详细地揭示腔内流激振荡特性,本文分别从脉动压力分布规律和腔口剪切层振荡特性进行分析,文中相对高度yi/H及各边名称的定义如图 3(a)~(c)所示。
4.1 脉动压力系数分布特性
4.1.1 脉动压力系数周向分布特性
深型陷落腔流体脉动压力系数的周向分布规律见图4,图5给出了高雷诺数时脉动压力系数的周向分布规律。
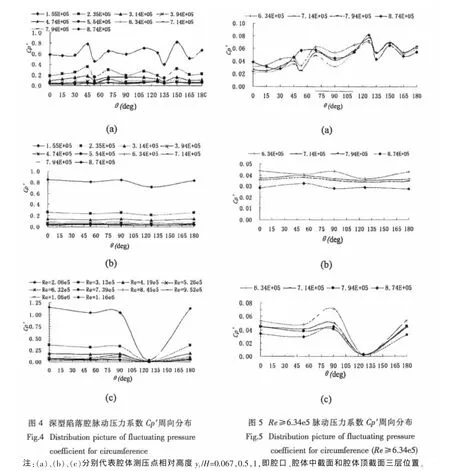
由图4(a)~(c)从整体上看Cp′在深型陷落腔内周向分布规律并不一致,但Cp′都随Re数的增加而减小。腔口处的脉动压力系数分布规律见图4(a)和图5(a),当来流流速很小时Cp′波动较大,随来流流速的增加Cp′的周向分布达到稳定(如(a)),当腔口处Cp′达到稳定时Cp′随θ的增加而略有增大,在腔口随边处(θ=127°~180°)的 Cp′比导边(θ=0°~53°)处的 Cp′大,且在随边角点(θ=127°)处 Cp′最大。呈现出随边的脉动力>侧面的脉动力>导边处的脉动力,这正证明了在陷落腔腔口处存在剪切层振荡现象,且越向下游随边处剪切层振荡越为强烈,所以腔口随边处存在着最大的Cp′。
由图4(b)和图5(b)与腔口处的脉动压力相比,深型陷落腔中截面处脉动压力的周向分布较为均匀,Cp′曲线趋于平坦(见图(b-2)及(a-2))。在相同雷诺数时腔中截面侧壁的Cp′远小于腔口随边处Cp′,但其值要略大于腔口导边处的Cp′。
由图4(c)和图5(c)可见无论是低雷诺数还是高雷诺数,深型陷落腔顶截面处的Cp′在θ=127°(即顶截面下游方向角点处)时陡降为0,而在其它侧点处Cp′值较接近。在实验数据分析中发现在θ=127°时稳态压力系数Cp=0,由此也可说明Cp′陡降为0的原因是在深型陷落腔腔顶截面下游角点处水流没有流动,所以脉动压力系数陡降为0。
4.1.2 脉动压力系数垂向分布特性
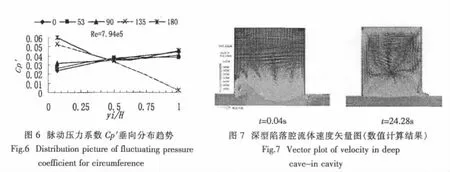
学者们更为关心的是脉动压力系数Cp′沿腔体深度方向的变化情况。由上述分析可知高雷诺数时深型陷落腔内Cp′分布趋于稳定,且不同雷诺数时脉动压力系数的垂向变化规律一致,因此图6以Re=7.94×105为例给出Cp′的垂向分布趋势。
由图6清晰可见在yi/H=0.067时θ=135°和180°(即腔口随边位置)处的Cp′脉动力最大。随边角点(θ=135°)处Cp′随相对高度的增加而减小,在顶截面处为0,而其它侧点处的脉动压力随相对高度的增加而略有增大,呈现出腔体顶截面处Cp′>中截面处Cp′>腔口导边及侧边处的Cp′。即深腔内部也存在着较大的脉动力。腔口随边处脉动力最大是因为随边正对于来流方向,其一是在腔口处剪切层振荡十分明显,其二是随边壁面会给予来流流体一反向阻力,所以腔口处随边脉动力较大;而顶截面处的流体受腔内循环水流运动的影响,逆时针运动的水流同样会因壁面给予的反向阻力而产生较大的脉动力(除下游面角点外)。为清晰地理解腔内的流动运动状态图7给出了深型陷落腔内流体运动初始时及稳定时的矢量图,以增加腔内流体运动的感性认识,鉴于数值计算的文章已发表[8],本文不再对数值计算方法及结果进行详细讨论。
4.2 深型陷落腔剪切层自持振荡特性
实验中存在各种干扰信号所以本文采用Matlab先滤掉各种干扰信号后,再对腔口处剪切层自持振荡的频率进行分析。图8给出了不同速度时深型陷落腔剪切层处脉动压力的自功率图。
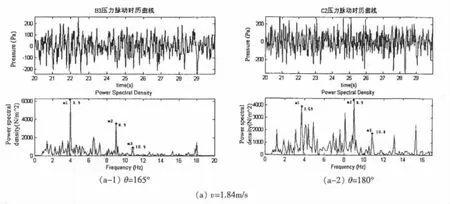
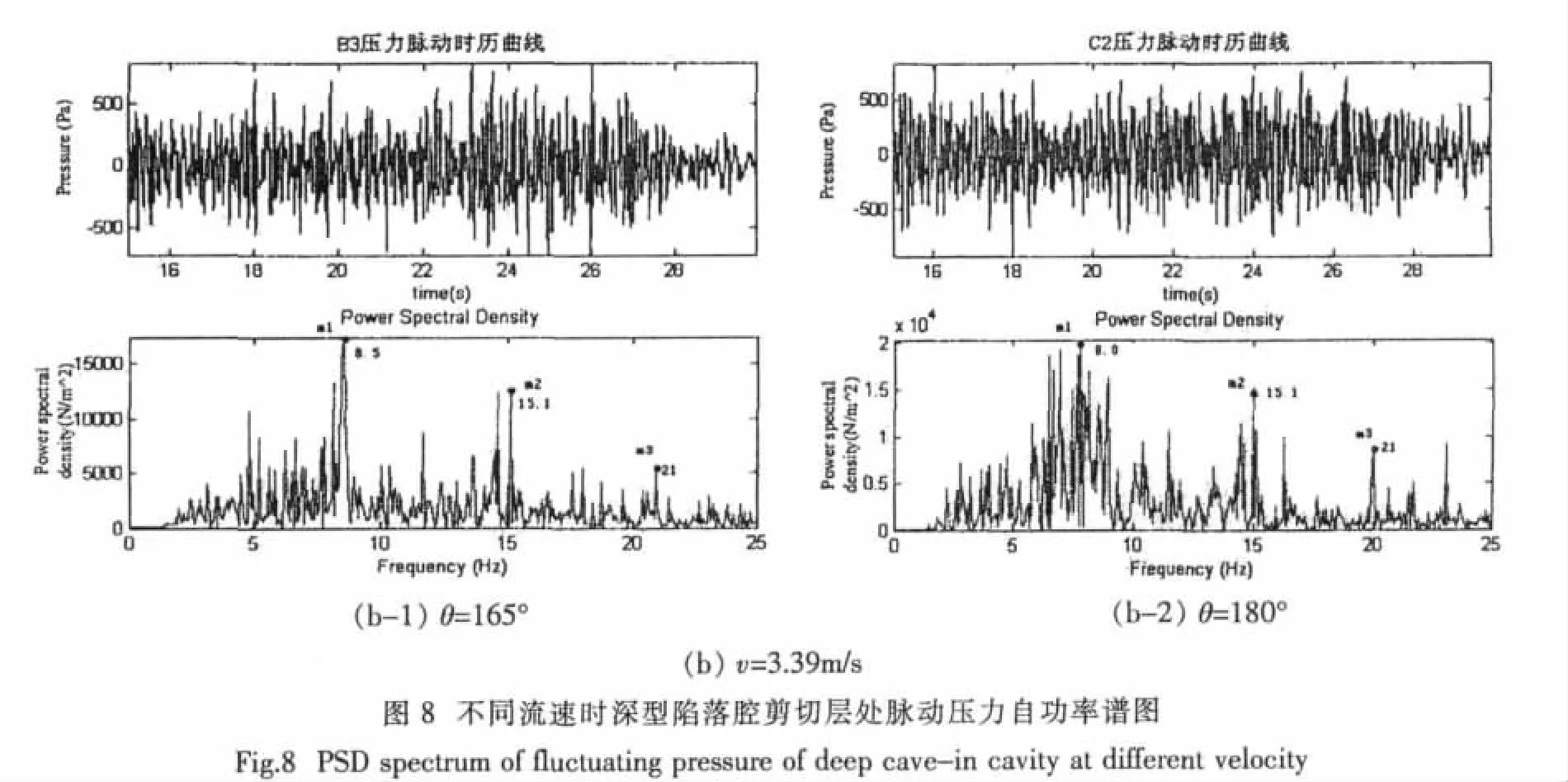

由图8(a)和(b)可见在相同来流流速时腔口剪切层随边处的振荡频率是基本一致的,随来流流速的增加剪切层随边处的振荡频率增大,脉动力明显地增强,这证实了脉动压力随Re数的增加而增强,Cp′随Re数的增加而减小。由公式(2)折算出各阶频率对应的St数随Re的变化为同一常数值。本文并根据实验数据采用最小二乘法对St~Re的曲线进行拟合,拟合公式见公式(4)。图9中给出了St数随Re的变化规律。
由图9可见相同阶的St数随Re数变化为同一常数,即
m1≈0.5,m2≈1.1,m3≈1.7。本文折算的St数比Rossiter[6]在低Ma数时研究的二维陷落腔剪切层振荡的 St数略大(m1≈0.42,m2≈1,m2≈1.57),与何祚镛[2]测得结果较为接近(m1≈0.55)。 但深型陷落腔的St数随Re数的变化规律与二维陷落腔的变化规律一致[2-6]。同时本文根据实验数据给出了深型陷落腔在均匀流场作用下St数的估算公式:

5 结 论
本文采用一系列的物理实验研究了深型陷落腔在均匀流场作用下脉动压力分布特性及剪切层振荡特性,主要得出以下结论:
(1)三维深型陷落腔内Cp′的周向分布都随Re数的增加而减小,但脉动压力随Re数的增加而增加。
(2)三维深型陷落腔腔口随边处的Cp′最大,且Cp′随相对高度的增加而减小,随边角点处的Cp′在yi/H=1时陡降为0;腔口导边及侧面的Cp′随相对高度的增加而略有增大,即深型陷落腔在顶截面处也存在着较大的脉动力。
(3)均匀流作用下三维深型陷落腔剪切层自持振荡各阶频率对应的St数随Re数的变化为一常数,此常数比气流场作用下的二维陷落腔的值略大。文中给出均匀流中三维深型陷落腔St数的估算公式。
[1]D’yachenko A Yu,Terekhov V I,Yarygina N I.Vortex formation and heat transfer in turbulent flow past a transverse cavity with inclined frontal and tear walls[J].International Journal of Heat and Mass Transfer,2008,51:3275-3286.
[2]何祚镛.结构振动与声辐射[M].哈尔滨:哈尔滨工程大学出版社,2001:147-182.
[3]康 庄.月池流噪声及水动力特性的实验研究[D].哈尔滨:哈尔滨工程大学,2006:4-100.
[4]朱习剑,衣云峰,何祚镛.突出腔的流激振荡激励源[J].哈尔滨船舶工程学院学报,1994,15(1):26-36.
[5]Jacquin,Geffroy.Large-eddy simulation of a subsonic cavity flow including asymmetric three-dimensional effects[J].Journal of Fluid Mechanics,2007,577:105-126.
[6]Rossiter J E.Wind tunnel experiments on the flow over rectangular cavities at subsonic and transonic speed[R].R.A.E.Tech.Report 64037,1964:210-235.
[7]Rowley C W,Wlliams D R.Dynamics and control of high-Reynolds number flow over open cavity[J].Annu.Rev.Fluid Mech,2006(8):251-276.
[8]姚熊亮,杨国晶,戴绍仕等.陷落腔剪切层自持振荡的数值计算分析[J].水动力学研究与进展,2009,24(3):332-340.
Experimental research on fluctuating pressure distribution of 3D cave-in cavity
DAI Shao-shi,YAO Xiong-liang,LI Zhuo
(College of Shipbuilding Engineering,Harbin Engineering University,Harbin 150001,China)
Aiming at fluid induced oscillation problem of 3D cave-in cavity owing to separation flow in uniform,a series of physical experiments was carried out.The range of Reynolds number is Re=1.55e5~8.74e5at zero attack angle of incoming.Circumferential and vertical fluid fluctuating pressures along the deep cavein cavity were measured,meanwhile,distribution of fluctuating pressure and oscillation characteristic of shear layer were analyzed.The results of experiment show that the distribution of fluctuating pressure in uniform field is complex.The fluctuating pressure at the leading edge of shear layer is the largest and fluctuating pressure at angular point drops to zero with the relative height increasing.But the fluctuating pressures at the leading edge and side increase a little with the increment of relative height.Moreover the change of St number of shear layer versus Re number is constant,but the value of St number is larger than the value of two dimensions in the air.
deep cave-in cavity;uniform flow;fluid induced oscillation;fluctuating pressure;experimental research
035
A
1007-7294(2010)05-0451-07
2009-11-17
哈尔滨工程大学国防科技工业技术基础科研项目(B1920070100)
戴绍仕(1976-),女,哈尔滨工程大学博士生,E-mail:daishaoshi@163.com。
book=457,ebook=44

