螺旋桨敞水性能CFD不确定度分析
杨仁友,沈泓萃,姚惠之
(中国船舶科学研究中心,江苏 无锡 214082)
螺旋桨敞水性能CFD不确定度分析
杨仁友,沈泓萃,姚惠之
(中国船舶科学研究中心,江苏 无锡 214082)
基于商用RANS代码,利用结构化网格技术和流道计算模型对库存螺旋桨敞水性能进行数值计算,并参考ITTC-CFD不确定度分析推荐规程和基准检验试验数据,对其水动力数值模拟结果进行验证和确认。文中为开展网格收敛性研究,共设计了三套网格,网格加细比为同时也分析比较了SST k-ω湍流模型和RNG kε湍流模型对网格收敛特性的影响,为螺旋桨敞水水动力数值模拟方法向工程应用方向迈进提供技术支撑。
螺旋桨;敞水性能;CFD;不确定度分析
1 引 言
随着计算机技术的不断发展和计算能力的不断提高,CFD技术逐渐成为船体外形选型、优化设计中的一个重要手段,而制约CFD工程上广泛应用的主要瓶颈是CFD技术的快速反应能力以及CFD技术的计算精度与结果可靠性问题。对于后者,国内外相关技术人员开展了深入和细致的研究工作,召开了多次学术会议,取得了许多成效,也初步提出了CFD不确定度分析的推荐规程。
目前,国际上通常采用Richardson外推法(RE)定量估算数值误差,它将误差看作典型网格单元尺寸的幂级数展开式。实际应用中,受到网格套数的约束,幂级数展开式不得不采用有限项数n来确定误差。根据RE公式可知,误差表达式中有1+2n个未知数,所以需要同等数目的数值解。理论上,项数n越大,网格越精细且更接近渐进范围。但是n的增大带来的不利影响是网格数目的增多。经典方法中,仅选取一项来满足渐进范围,如Roache等[1]提出的网格收敛指标(GCI)方法。该方法将单项幂级数指数p看作未知,由于程序中包含三个未知数:精确解φ0、系数α和准确度量阶p,因此至少需要三套网格才能开展网格收敛性研究,像Stern[2]和24届ITTC[3]等均推荐此方法开展CFD不确定度分析。另一种方法是由Oberkampf[4]建议的采用给定整数指数的多项幂级数方法。当取一项幂级数展开时,需要两套网格;取两项幂级数展开时,需要三套网格;三项之时,需要四套网格,依此类推。文献[4]通过算例进行两种方法对比分析认为,采用Roache的未知指数单项展开式和给定指数的两项展开式来估算误差似乎是最为有效。Eça和Hoekstra[4]提出采用最小二乘法来计算上述各未知参数值,其所需网格套数至少比上述方法多一套。最小二乘法可用于处理因网格几何相似性较差而导致计算结果离散度较大的方案。
不确定度定义的目的是保证某置信区间内真实误差在估计误差+/-不确定度U的范围内。为了估算利用RE方法得到的误差,必须确定其不确定度。对此,ITTC推荐规程[2]提出了修正因子法,该修正因子Ck的概念是建立在一维波动方程、二维拉普拉斯方程以及布拉休斯边界层解析解的验证研究之上的。然而当Ck在1附近时,规程建议采用Roache的安全因子FS来估算不确定度。考虑到FS是经验给出的,Eça等人[4]提出了安全因子的估算方法。
在进行CFD不确定度分析过程中,为了采用RE方法外推得到零尺度网格数值精确解,要求所有网格具有良好的几何相似性,这就使得目前绝大部分CFD不确定度分析主要针对结构化网格技术且对象几何相对较为简单的方案。如Eça[5]开展了绕小山丘的二维湍流流动、三维有限平板流动和KVLCC2M油轮三维湍流流动的数值计算和不确定度分析。该论文主要进行了迭代误差的估算方法研究,以及分析迭代误差对离散误差的影响。Weymouth[6]进行了Wigley船升沉和纵倾运动工况的数值模拟,并利用ITTC推荐规程进行了时间步长、网格收敛性等的不确定度分析。Van[7]针对DARPA SUBOFF潜艇模型同样利用ITTC推荐规程开展了阻力的CFD不确定度分析。Simonsen等[8-9]尝试采用嵌入式网格对带舵Esso Osaka油轮的水动力和流场进行CFD不确定度分析。以上以Richardson外推法为基础的各种CFD不确定度分析主要针对结构化网格且假设计算结果具有良好渐进范围为基础开展工作的,其应用局限性较大。鉴于此,Zhang[10],Celik[11-12]及Qin和Shih[13]等提出采用误差输运方程(ETEs)方法进行CFD误差估算。它通过将误差输运方程与流动控制方程一起求解,求导分析残差或者输运方程的误差源项来监控计算误差,它可以在计算过程中或者后处理过程中进行CFD误差分析。正如24届ITTC阻力委员会总结报告[14]所言,由于ETEs方法具有处理分析包括非结构化网格在内的复杂几何网格的能力,或许在未来该方法将变得更加普遍。
虽然ITTC推荐的CFD不确定度分析规程尚未得到广大专家的一致同意,但考虑到该规程目前使用比较广泛、而且执行程序相对比较简单,因此本文还是尝试采用ITTC推荐规程,开展螺旋桨敞水水动力的CFD不确定度分析,并分别采用SST k-ω和RNG k-ε湍流模型分析计算CFD不确定度。
2 研究对象与计算网格
本文以库存螺旋桨模型为对象计算分析。该桨模直径为0.2m,0.7R处叶片螺距比达1.2,右旋桨。
采用商用前处理软件Gambit生成多块结构化网格,其中,对于桨叶附近区域,针对不同半径区域进行分段建模,各网格块之间采用对接网格技术进行连接;导流帽和螺旋桨尾流段区域也同样采用结构化网格,各区域网格采用交接面形式进行搭接。至于网格形式,在桨叶附近区域沿叶片弦长方向为O型网格,沿径向方向为H型网格,在计算域其余区域沿纵向(即螺旋桨旋转轴)方向为H型网格,沿周向为O型网格,如图1所示。
文中共建立了三套(m=3)网格,三套网格尺度如表1所示,桨叶壁面网格节点分布如图2所示,网格加细比为rk=


表1 网格节点设置及网格数Tab.1 The grid numbers and the node sets

3 计算方法
本文敞水螺旋桨CFD计算方法描述如下:
a.采用单个桨叶流道计算模型,桨叶叶片旋转模拟采用多参考系模型(MRF)。
b.计算域大小为6D×12D×6D(如图3所示);边界条件主要包括速度入口、压力出口、外场边界、流道两侧周期性边界条件及桨叶壁面无滑移边界条件。
c.整个计算域采用H-O型多块结构化网格。
d.选用隐式格式来放宽稳定性限制,对流项采用二阶迎风格式,扩散项采用中心差分格式;压力、速度耦合采用SIPMLE算法。
e.采用了两种湍流模型SST k-ω和RNG k-ε。

4 CFD不确定度分析程序
由ITTC推荐规程—CFD中的不确定度分析—验证和确认的方法及规程[3]可知,CFD不确定度包括模型误差δSM和数值误差δSN,这与试验不确定度中包含的系统误差和随机误差相类似。
CFD不确定度分析包含验证与确认两个程序。验证就是计算数值模拟的数值误差δSN和数值不确定度USN;确认就是利用基准试验数据评估数值模拟的模型不确定度USM的过程。本文根据ITTC推荐规程—CFD中的不确定度分析—验证和确认的方法及规程[3]和规程提供的阻力与流场分析范例[15],开展敞水螺旋桨CFD不确定度分析。
4.1 CFD验证程序
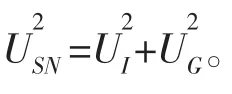
文献[5]针对三种迭代误差估算方法L∞、L1和L2范数比较得出,由于L∞范数相当于外推至无限迭代步数,大大改善了迭代误差估算能力。因此本文采用L∞范数估算迭代不确定度,即

式中,收敛判据为离散方程残差达到10-4。
对于离散误差,主要通过Roache的GCI方法进行研究。用一阶的RE估计、准确度量阶p、修k正因子Ck和收敛率Rk。即
式中,下标k表示网格组类,下标1、2、3分别表示该组由密到疏的三套网格;pest是当空间步长趋于0、渐进范围为Ck→1时,首项准确度极限阶数的估计值,本文取为2。
当收敛率Rk>1之时,收敛状态发散。
当收敛率Rk<0时,波动收敛,不确定度可以简单估计为基于波动最大值SU和最小值SL的限定误差,即

当收敛率0<Rk<1时,单调收敛。不确定度按下述方法估计:
若将Ck看作缺少置信度时远小于1或者远大于1情况,那么网格不确定度UG得到估计,但没有估计 δG,


若将Ck看作存在置信度时接近于1的情况,则和都得到了估计,当式Ck=1时,(9)式中UGC=0,这是不现实的。因此对于Ck=1,ITTC规程建议使用安全因子法,


4.2 CFD确认程序
确认的过程就是利用基准验证试验评估数值模拟的模型不确定度USM的过程。对于基准验证试验而言,需要模型测试结果D和测试不确定度UD。
对比误差E是由试验数据D和模拟值S之差给出,

安全因子的准确值是模糊的,对于细致的网格研究,建议FS取1.25;对于只使用两种网格且准确度量阶是根据理论值pth得到的情况,建议FS取3。修正解SC为因此,通过比较E与确认不确定度UV就能判定确认实现与否。其中,

如若 UV<,表明对比水平高于噪声水平,模拟结果没有得到确认。当UV<<时,说明模型误差是主要不确定度源,因此可以利用E=δSM来改进模型。
5 螺旋桨水动力的CFD验证与确认

文中分别采用了SST k-ω和RNG k-ε两种湍流模型,开展螺旋桨推力、扭矩与其摩擦和压差水动力分量及敞水效率的不确定度分析工作。
5.1 SST k-ω湍流模型CFD不确定度分析
5.1.1 验证
借助螺旋桨推力系数、扭矩系数的迭代历程曲线来评估迭代收敛性。图4给出了网格1在收敛判据达到10-4工况,Np=1 000迭代步数内的迭代历程曲线。由公式(1)可得其推力、扭矩迭代不确定度分别为1×10-6D和9×10-7D。同理可以得到网格2推力、扭矩迭代不确定度分别为3×10-5D和1×10-5D,网格3推力、扭矩迭代不确定度分别为2×10-6D和4×10-6D。与网格误差相比,上述三套网格的迭代不确定度至少小两个数量级,因此可以假定迭代误差和迭代不确定度忽略不计。
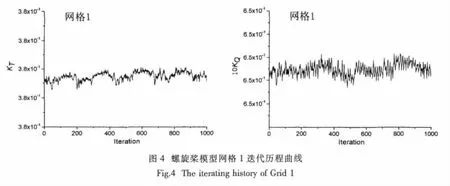
三套网格螺旋桨推力系数KT及其分量KTf和KTp、扭矩系数KQ及其分量KQf和KQp、敞水效率η0的计算结果和试验数据如表2所示。
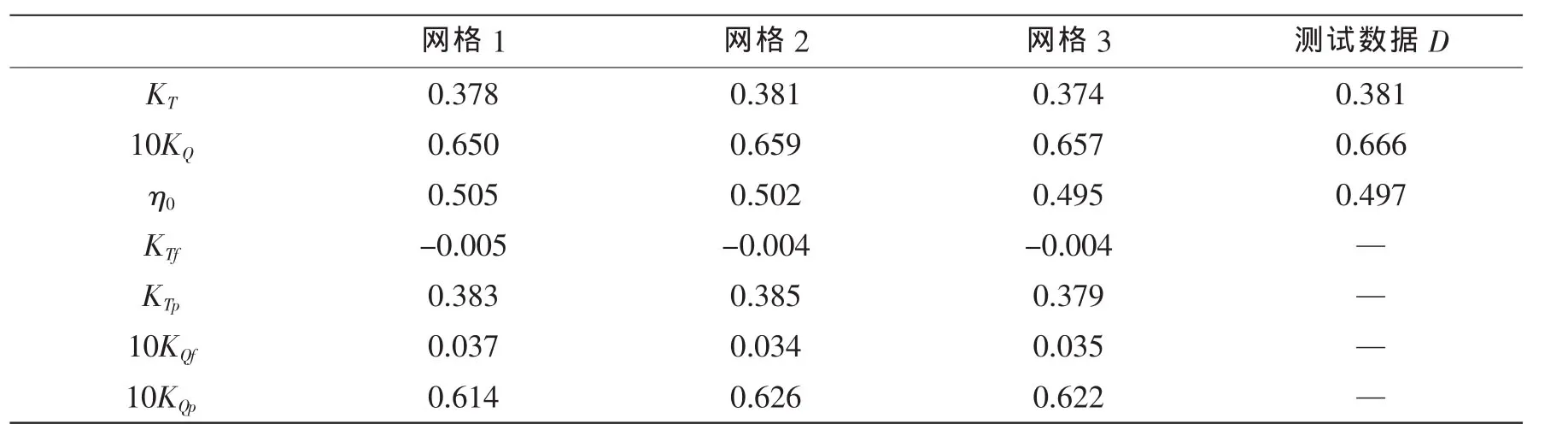
表2 敞水螺旋桨水动力性能计算与试验结果列表(SST k-ω)Tab.2 The numerical results and experimental data of the open-water performance of the propeller(SST k-ω)
利用4.2节提供的验证程序,估算得到敞水螺旋桨水动力性能CFD不确定度分析结果,如表3所示。其中,对于单调收敛情况,文中所进行的不确定度与误差估计不但考虑了在缺少置信度下Ck远小于1或远大于1的情况,而且考虑了存在置信度时Ck接近于1的情况。
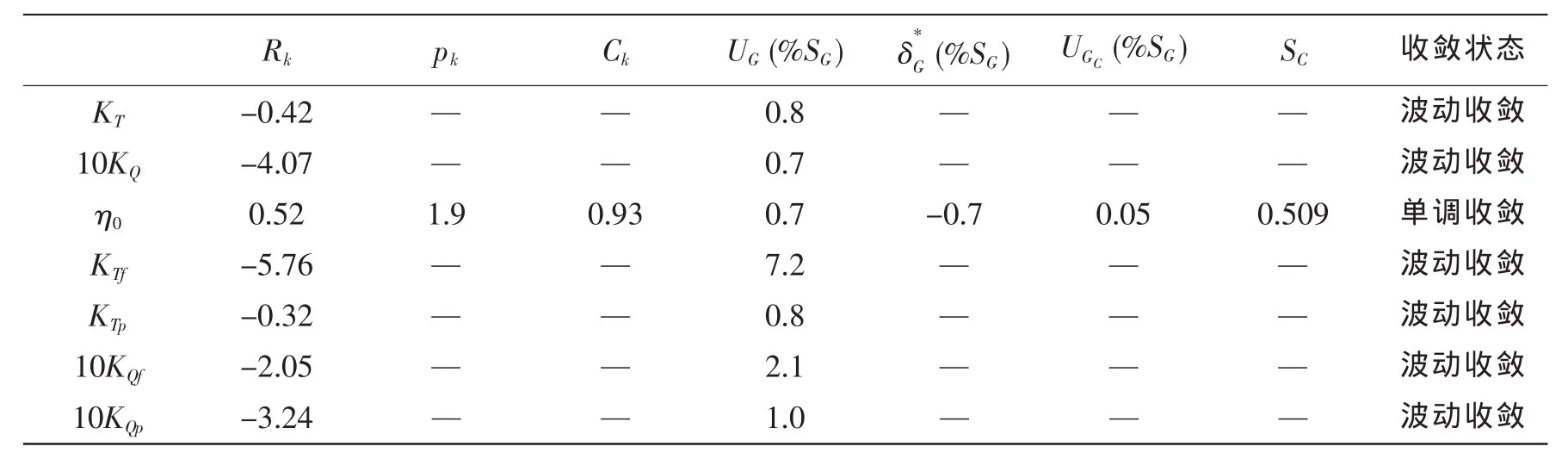
表3 敞水螺旋桨水动力的验证(SST k-ω)Tab.3 The verification of the open-water performance of the propeller(SST k-ω)
从表中可以看出,针对敞水螺旋桨三个水动力测试参数,其验证水平相对较小,均小于1%,螺旋桨压差力验证水平也均在1%以内。而对于螺旋桨水动力分量—摩擦力,由于其大小要小两个量级左右,网格迭代误差以及计算机精度等对其影响不可忽略,故其验证水平要高一些。
5.1.2 确认
确认过程需要用到模拟预报值S,若进行了修正还需用到修正后的模拟预报值SC。同时,为了评估模拟结果有无得到确认,需要模型测试结果D和测试不确定度UD。利用4.3节CFD确认程序,计算得到的结果如表4所示。

表4 螺旋桨敞水水动力确认过程(SST k-ω)Tab.4 The validation of the open-water performance of the propeller(SST k-ω)
由表中数据可知,对于推力系数KT,对比误差<UV,说明模拟结果得到确认。USN<<UD表明 KT测试误差是主要不确定度源之一。
对于扭矩系数KQ,对比误差>UV,表明模拟结果没有得到确认。USN<<UV说明网格分辨率已基本满足计算要求,因此要减小UV就要减小UD。对比误差E大于0,说明模拟预报结果偏低。E与UV同量级,因此尚不能判断模拟预报结果偏低是模型误差引起的还是试验误差所致。
5.2 RNG k-ε湍流模型CFD不确定度分析
5.2.1 验证
与5.1节相类似,三套网格采用RNG k-ε湍流模型计算得到的推力、扭矩迭代不确定度结果如表5所示。

表5 RNG k-ε湍流模型计算迭代不确定度UI研究Tab.5 The iterating uncertainty UIcomputed by RNG k-ε turbulent model
通过与网格不确定度UG比较可知,迭代不确定度UI至少要小一个量级,因此可以忽略UI的影响,即USN≈UG。
采用RNG k-ε湍流模型模拟得到的三套网格螺旋桨推力系数KT及其分量KTf和KTp、扭矩系数KQ及其分量KQf和KQp、敞水效率η0的计算结果和试验数据如表6所示,不确定度验证水平如表7所示。

表6 螺旋桨敞水水动力计算与试验结果列表(RNG k-ε)Tab.6 The numerical results and experimental data of the open-water performance of the propeller (RNG k-ε)

表7 敞水螺旋桨水动力的验证(RNG k-ε)Tab.7 The verification of the open-water performance of the propeller (RNG k-ε)
由表7可知,敞水螺旋桨推力系数KT、扭矩系数10KQ及敞水效率η0呈单调收敛状态。其中,KT未修正时,网格不确定度UG达到1.3%,修正后降低至0.5%;10KQ的网格相对不确定度相当低,在0.1%的量级;对于敞水效率η0,其相对网格不确定度达到4%左右。而对于推力、扭矩摩擦分量,由于其量级相对比小两个量级左右,迭代误差以及计算机精度等对其影响不可忽略,使其收敛状态呈发散。至于推力、扭矩压力分量,特别是扭矩压力分量KQp,其收敛率Rk小于0,但接近于0,表明KQp虽然呈波动收敛状态,但其解是向解的渐进区域靠近的。
与5.1节SST k-ω湍流模型模拟计算的验证水平比较可以看出,湍流模型不仅对网格不确定度大小有一定影响,而且对网格收敛状态也有较大影响,即湍流模型与网格收敛性研究存在耦合。5.2.2确认
利用4.3节确认程序对表7 CFD验证数据进行确认分析,结果如表8所示。可以看出,不管是推力系数KT,还是扭矩系数KQ,E均小于UV,表明模拟结果得到确认。对于KT,未修正时,对比误差E仅是UV的1/3,修正后EC<<UVC,表明提高网格分辨率对于改善KT预报能力是有利的,但改善幅度不大(1%的量级),因此若要降低UV就要减小试验的不确定度UD。对于KQ,E≈EC表明提高网格分辨率对于改善KQ预报精度已基本无效果。

表8 螺旋桨敞水水动力确认过程(RNG k-ε)Tab.8 The validation of the open-water performance of the propeller(RNG k-ε)
6 结 语
本文基于ITTC推荐的CFD不确定度分析规程对库存螺旋桨敞水水动力数值计算结果进行了不确定度分析,尝试分析了SST k-ω和RNG k-ε两种不同的湍流模型对CFD不确定度的影响。针对文中三套网格方案,基于文中分析结果可得:
a.湍流模型与网格收敛性存在交互,它不仅对网格不确定度大小有影响,甚至关系到网格收敛状态。
b.采用文中建立的数值方法和网格数量计算得到的网格误差远小于试验误差,表明本文采用的网格分辨率能够满足敞水水动力数值计算精度要求。
c.由于螺旋桨敞水水动力摩擦分量比压差力小两个量级,使得迭代误差和计算机精度等对其影响不可忽略,因此在进行网格收敛性研究时网格不确定度较大或者呈发散状态。
[1]Roache P J.Verification and validation in computational science and engineering[M].Hermosa Publishers,1998.
[2]Stern F,Wilson R,Coleman H W,Paterson E G.Comprehensive approach to verification and validation of CFD simulations-Part 1:Methodologies and procedures[J].ASME Journal of Fluids Engineering,2001,123:803-810.
[3]ITTC Quality Manual[K].7.5-03-01-01,2005.
[4]Eça L,Hoekstra M.An evaluation of verification procedures for CFD applications[C]//24th Symposium on Naval Hydrodynamics,8-13 July 2002.Fukuoka,Japan,2002.
[5]Eça L,Hoekstra M.On the influence of the iterative error in the numerical uncertainty of ship viscous flow calculation[C]//26th Symposium on Naval Hydrodynamics,17-22 September 2006.Rome,Italy,2006.
[6]Weymouth G D,Wilson R V,Stern F.RANS CFD prediction of pitch and heave ship motions in head seas[C]//Proc.8th Int.Conf.Numerical Ship Hydrodynamics.Busan,Korea,2003.
[7]Van S H,Kim J,Park I R,Kim W J.Calculation of turbulence flows around a submarine for the prediction of hydrodynamic performance[C]//Proc.8th Int.Conf.Numerical Ship Hydrodynamics.Busan,Korea,2003.
[8]Simonsen C D,Stern F.Verification and validation of RANS maneuvering simulation of Esso Osaka:Effects of Drift and Rudder angle forces and Moments[J].Computers and Fluids,2003a,32:1325-1356.
[9]Simonsen C D,Stern F.Flow pattern around an appended tanker hull form in simple maneuvering conditions[C]//Proc.8th Int.Conf.Numerical Ship Hydrodynamics.Busan,Korea,2003b.
[10]Zhang X D,Pelletier D,Trepanier J Y,Camarero R.Numerical assessment of error estimators for Euler equations[J].AIAA J,2001,39(9):1706-1715.
[11]Celik I,Hu G,Badeau A.Further refinement and benchmarking of a single-grid error estimation technique[J].Paper No.AIAA-2003-0628,2003a.
[12]Celik I,Hu G.Single grid error estimation using error transport equation-to appear[J].J of Fluids Engineering,2004,126(5):778-790.
[13]Qin Y,Shih T T P.A discrete transport equation for error estimation in CFD[J].AIAA Paper No.2002-0906,2002.
[14]The Resistance Committee.Final Report and Recommendations to the 24th ITTC[C].Proceeding of the 24th ITTC-2005,I.
[15]ITTC-Recommended Procedures[K].7.5-03-02-01,2005.
Uncertain analysis of CFD simulation on the open-water performance of the propeller
YANG Ren-you,SHEN Hong-cui,YAO Hui-zhi
(China Ship Scientific Research Center,Wuxi 214082,China)
Using the structured-grid technology and the flow model around one blade passage,the hydrodynamic performance of the stock propeller was numerically computed with commercial RANS methods.According to the uncertainty analysis methology and procedure in CFD recommended by ITTC and the benchmark database,the numerical hydrodynamic results were verified and validated.In this paper,grid studies were conducted using three grids(m=3)with grid refinement ratio rk=,and SST k-ω and RNG k-ε turbulent models were solved respectively to analyze the turbulent-model effects on the grid-convergence characteristics.The objectives are to promote the numerical simulation levels in the practice of the open-water performance of the propeller.
propeller;open-water performance;CFD;uncertainty analysis
U661.3
A
1007-7294(2010)05-0472-09
2010-01-25
杨仁友(1980-),男,中国船舶科学研究中心博士研究生。

