深海耐压结构观察窗蠕变变形分析
田常录,胡 勇,刘道启,崔维成
(1江南大学机械学院,江苏 无锡 214122;2中国船舶科学研究中心,江苏 无锡214082;3北京交通大学,北京 100044)
深海耐压结构观察窗蠕变变形分析
田常录1,胡 勇2,刘道启3,崔维成2
(1江南大学机械学院,江苏 无锡 214122;2中国船舶科学研究中心,江苏 无锡214082;3北京交通大学,北京 100044)
大深度耐压开口结构的设计问题是深海探测装备研制过程中的关键技术问题之一。作者曾针对深海耐压开口结构的受力变形、蠕变以及耐压壳体变形协调等问题进行了计算分析和试验研究,并给出了观察窗应力的理论计算方法。文中进一步从理论上给出观察窗变形分析的计算方法和观察窗蠕变变形的计算公式。由此可对深海耐压开口壳体接触界面变形协调与水密技术进行理论方面的探索研究,为形成深海耐压开口结构优化设计的理论计算方法及相关技术标准的制定提供理论方面的支撑。
深海载人潜水器;观察窗;蠕变计算
1 引 言
载人球开口结构设计是深海载人潜水器结构设计的关键技术之一。文献[1]针对大深度载人潜水器的观察窗,采用计算分析和试验研究两种手段对大深度潜水器观察窗的蠕变特性进行了研究。观察窗蠕变与受压时间、外载荷、观察窗与金属窗座的接触几何形式、接触面的润滑状态等因素均有关系。文献[2]针对大深度载人潜水器的观察窗,给出了观察窗的应力计算方法。本文基于文献[2]的应力计算方法,对潜水器观察窗的蠕变变形理论方面展开进一步的探索,并推导获得了观察窗受力变形的理论公式以及观察窗蠕变变形的计算公式。
载人球开口结构主要有观察窗和人员出入舱口两种。对于“和谐号”,其载人球内直径2.1m,设有一只透光直径为200mm的主观察窗和两只透光直径为120mm的侧观察窗。主、侧观察窗都采用45°锥体结构。观察窗的锥形面和窗座锥形面均进行了打磨处理,接触边界非常光滑,摩擦系数很小,约为f=0.1。
对于载人潜水器耐压结构,主要考虑其短期潜水后再次浮起的工况,此时观察窗与壳体接触界面变形协调与水密性能是设计者关心的。在此工况下,观察窗压力实验[1]表明,外压消除后,观察窗几乎能够恢复到初始位移状态。因而,可设观察窗体的蠕变为随时间变化的非线性弹性变形,可按非线性粘弹性变形进行分析。
2 有机玻璃和观察窗的蠕变试验结果
2.1 有机玻璃的蠕变变形
观察窗的制造材料为有机玻璃。有机玻璃材料是一种粘弹性体材料,在海水压力作用下会发生变形随时间增加现象,即蠕变现象。这种现象的特征是变形、应力与外力不再保持一一对应关系。对于粘弹性材料的本构关系常见的有Maxwell模型、Kelvin模型、标准线性体模型、Burgers模型、多元件模型等等。粘弹性模型中组成的元件增多,就能够更加准确地描述材料的实际特性,文献[3]通过系列试验数据得到在常温下有机玻璃蠕变的回归公式。

其中:ε为应变,εc为临界断裂应变,t为时间,tc为临界断裂时间。εc和tc与应力水平相关。表1为不同应力水平下,拉伸试棒的临界断裂应变εc和临界断裂时间tc试验测试结果。
根据试验数据,在常温下εc、tc可以回归成下列计算公式:

(1)、(2)式可合写为:

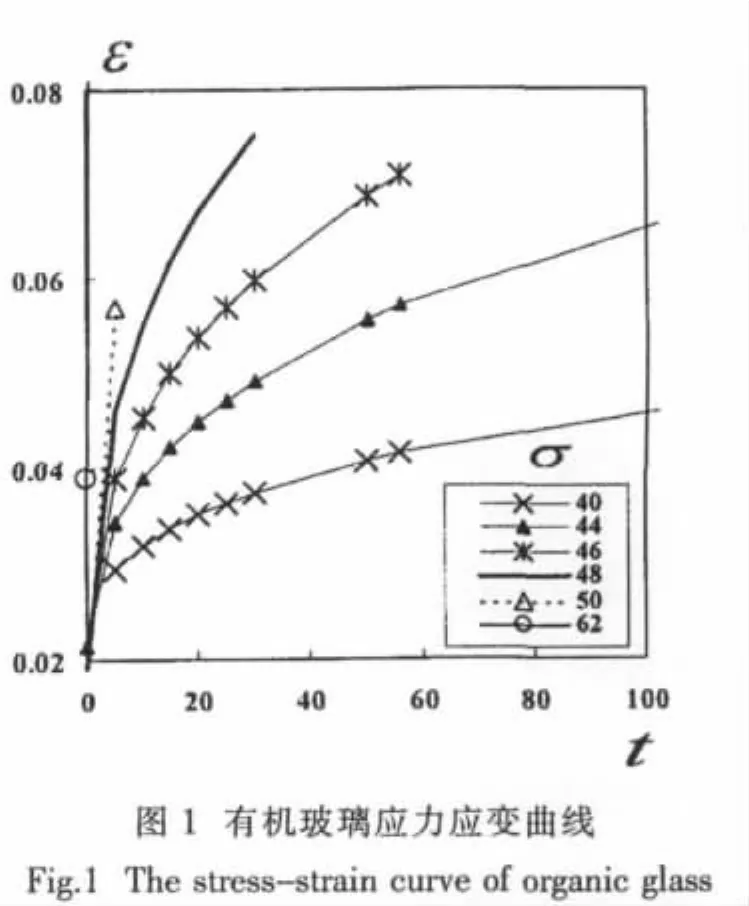
即为观察窗有机玻璃蠕变的应力-应变关系式,其分布见图1。
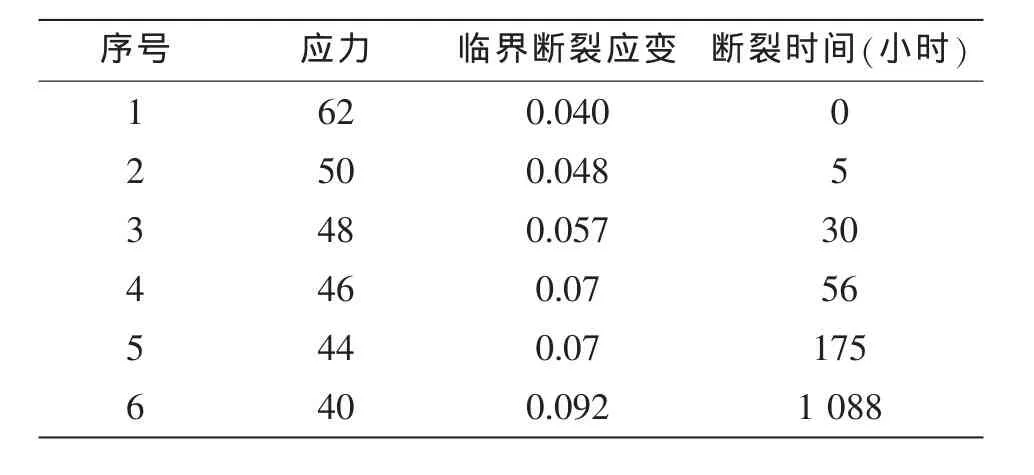
表1 有机玻璃应力水平与临界断裂应变、断裂时间试验结果Tab.1 The test results of critical fracture strain and time under different stress level for organic glass
2.2 观察窗蠕变的试验研究
文献[1]给出了侧观察窗和主观察窗的试验结果。观察窗在装配时喷涂润滑脂润滑,在观察窗的上下表面分别贴了3对双向应变片。在观察窗的下表面圆心处安装位移传感器,测量观察窗的轴向位移。通过保压来考核观察窗在工作深度下的蠕变特性。图2是在71.6MPa工作压力下侧观察窗、主观察窗分别保压9小时和6小时的蠕变测量结果。


3 观察窗的应力状态
文献[2]导出了观察窗应力,其轴向应力为:

径向应力为:

由于主、侧观察窗几何尺寸和受力形式都相似,就"和谐号"二观察窗为例,在无量纲坐标z/h中,主、侧观察窗无量纲轴向应力σz/q完全相同。观察窗任一点应力状态图如图3所示。
三主应力为:

应力偏量为:

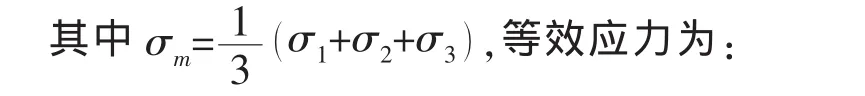
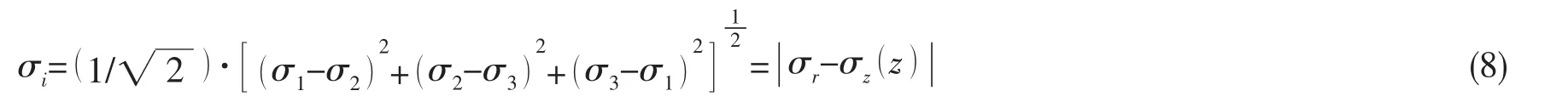
其中,轴向应力、径向应力分别由(4)、(5)式计算。
此外,由轴向应变分析和有限元计算均发现[1],体积应变相对较小,而且体积变形引起的轴向位移使观察窗外半段压缩、内半段伸长,因而体积变形引起的轴向位移很小。以下分析均忽略体积变形。
4 观察窗变形分析
4.1 观察窗轴向蠕变变形分析-粘弹性方法
蠕变理论复杂、分析方法众多。但潜水器观察窗的蠕变为随时间变化的非线性弹性变形。由于塑性力学的全量理论就是非线性弹性方法,因而,本问题的蠕变可按全量理论方法进行分析。设一维的蠕变应力应变关系为:

忽略体积应变,复杂应力状态的应力应变关系为:

其中,Sij为应力偏量,εi,σi为等效应变和等效应力。 按单一曲线假设,εi,σi和一维应力应变有同样的规律:

对于本文观察窗,其应力状态在3节已得到,由(7)、(8)式和(10)式,可得蠕变变形引起的轴向应变为:
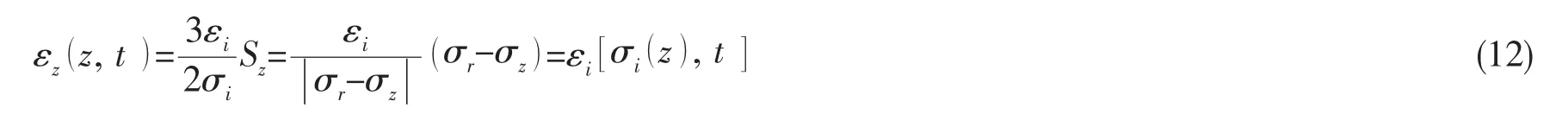
可见,轴向应变与等效应变在数值上相同。因而,轴向蠕变变形量为:
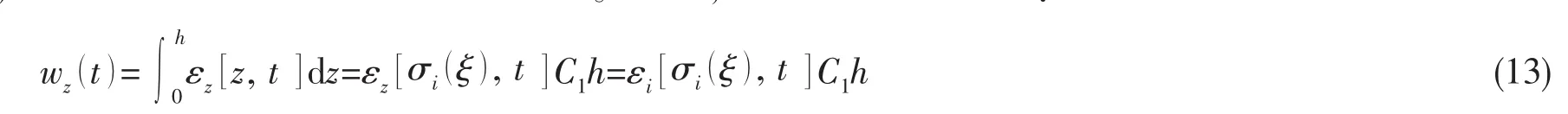
其中,ξ为积分特征点,C1为待定系数,与ξ取的位置有关。此式的意义可解释为积分值等于被积函数某特征点值乘以积分区间h和一权值系数C1。
就“和谐号”观察窗为例,有 α=π/4,f=0.1,侧观察窗 h=130,D1=380,主观察窗 h=220,D1=640。 典型地,取 ξ=0.9h,代入(4)、(5)式可得:

此式代入(8)式,可得等效应力与潜水器外压q的关系:

从而在特征点有:

按全量理论的单一曲线假设,(11)式的εi=εiσi,()t和一维应力应变的(9)式ε=ε σ,()t有同样的规律,通过参数变换σ=0.65q,就可得:

从而可得到针对潜水器观察窗轴向应变与潜水器外压q的关系:

其分布如图4和表2所示。
针对潜水器观察窗,就可直接应用(17)式,即图4或表2,不必再用2.1节有机玻璃的一维应力应变曲线(图1或表1)。(17)式代入(13)式,可得:

式中w为观察窗轴向位移,q为潜水器外压,t为时间,h为观察窗厚度,εz=εzq,(t)为图4或表2。权值系数C1由实验确定。

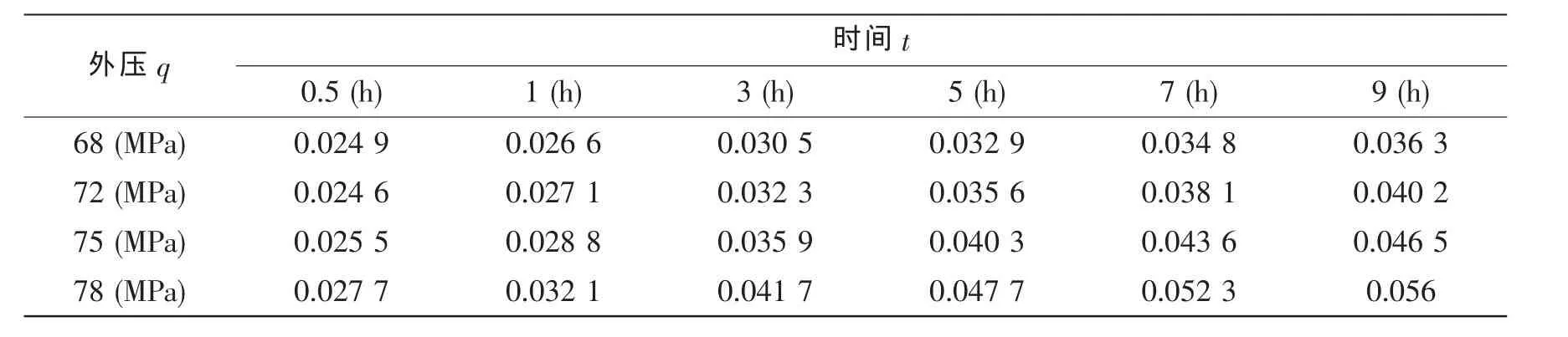
表2 潜水器观察窗轴向应变与潜水器外压q的关系εz=εz(q,t)Tab.2 Axial displacements of viewport windows versus out pressure for εz=εz(q,t)
4.2 观察窗轴向蠕变变形分析-几何方法
观察窗与窗座之间是面-面接触,对于用有机玻璃材料制成的观察窗,接触面上的钛合金观察窗窗座可以设定为刚性体,观察窗为粘弹性体材料。因而,观察窗的边界(即观察窗座)可认为是固定的。由此可知,潜水器观察窗的蠕变变形实际上是限制在特定形状下的一种特殊形式的变形,而固定边界的定形状也是已知的,即为观察窗座。

设D、w为高度为z处观察窗直径和轴向位移。取一微段dz,在z+dz处,直径为D+dD,轴向位移为w+dw,见图 5。
忽略体积应变,观察窗整体服从不可压缩规律,因而有:
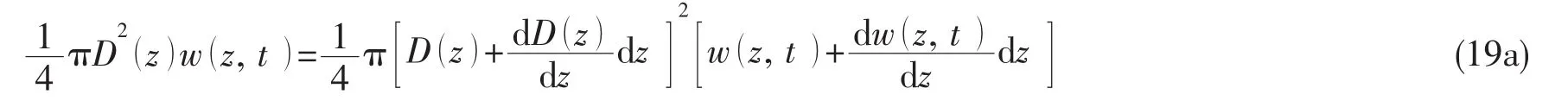
把w看成D的函数,则简化为:

略去高阶量得:

w是高度为z处观察窗轴向位移,D是高度为z处观察窗直径,其表达式为:

(20)式积分有:

C2为待定系数。在z=0时有D()z=D1,因而:

待定系数C2和上节的粘弹性变形关联。
5 观察窗轴向蠕变位移
5.1 观察窗轴向位移计算的理论方法
4.2节(23)式中的待定系数C2和4.1节(18)式待定系数C1有关,都应和粘弹性变形关联。比较(23)式和(18)式可得:

因而有:

在q=71.6MPa,t=10h时,由4.1节图4表2可知:

在q=71.6MPa,t=10h时,由2.3节图2(a)的实验结果可知:

把(26)、(27)式代入(25)式,注意此时 z=h=130mm,D=D1可得:

从而确定了待定系数。其中,D2为观察窗外内表面直径,此结果表明观察窗轴向蠕变位移与其小口直径成正比,D0为参考值,数值等于球壳直径。从而有观察窗轴向蠕变位移的计算公式:

式中,D是高度为z处观察窗直径,把(21)式代入(29)式得:

至此,我们形成了一套观察窗变形分析的理论计算方法、并且获得了观察窗蠕变轴向位移的计算公式,即(30)式。其中,D1,D2为观察窗外表面直径、内表面直径,h为其厚度,D0=2.1m为参考值,数值等于球壳直径。εz=εz(q,t)即为4.1节图4或表2。
5.2 观察窗轴向位移的计算结果分析
分别令z=0、z=h,由(30)式可得观察窗轴向最大、最小位移分别为:

球壳直径D0=2.1m=2100mm,其它数据为:
(1)侧观察窗有:h=130mm,D1=380mm,D2=120mm,由 4.1节图 4或表 2可知在 q=71.6MPa、t=10h时εz(q,t)=0.040 2;
(2)主观察窗有:h=220mm,D1=640mm,D2=200mm,由 4.1节图 4或表 2可知在 q=71.6MPa、t=5h时εz(q,t)=0.035 6。
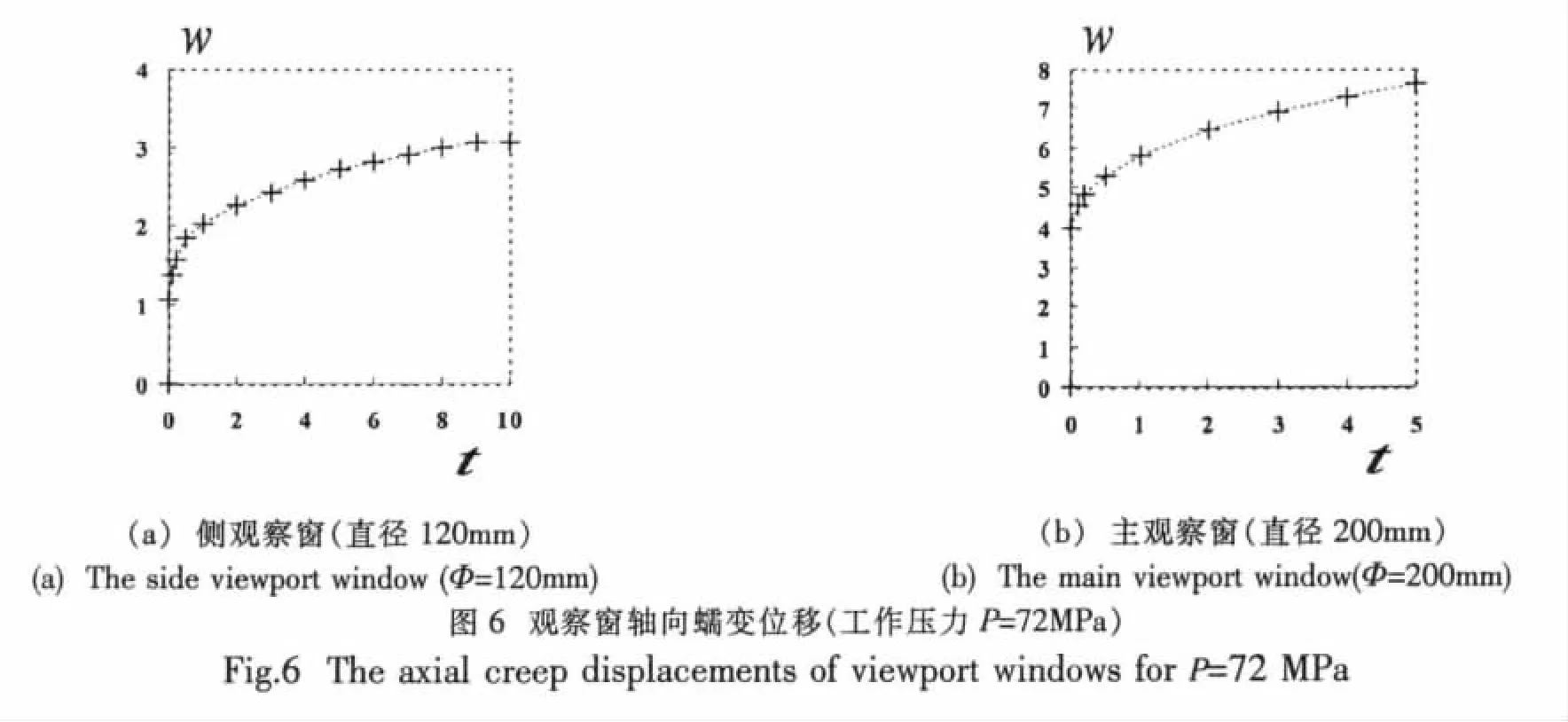
把以上两观察窗数据代入(31)右式,则可得到两观察窗的最大位移分布,即图6。特别是,在观察窗内外表面,是其最大和最小位移。对于侧观察窗,最大、最小位移分别为:

由于权值系数C≈D2/D0就是由该实验值确定的,因而wmax=3.1mm与实验值相符是必然的。
对于主观察窗最大、最小位移分别为:

与2.3节图3对比,可发现主观察窗最大位移与实验值也是相符的。可见,(30)式可统一描述不同形式观察窗的轴向蠕变位移,对于两种观察窗的计算结果都与实验值相吻合。
6 结 论
本文对深海水压下耐压开口结构观察窗的受力变形、结构蠕变、接触摩擦等问题进行了理论方面的探索。针对大深度载人潜水器的观察窗,给出了观察窗变形分析的理论计算方法和观察窗蠕变轴向位移的计算公式,该公式可统一描述和计算不同形式观察窗的轴向蠕变位移,其计算结果与实验结果相吻合。本文研究结果作为深海耐压开口壳体接触界面变形协调与水密技术研究的一部分、为深海耐压开口结构优化设计和相关技术标准的制定提供理论基础。
[1]刘道启,胡 勇,王 芳,田常录,崔维成.深海载人潜水器观察窗的蠕变特性[C].全国船舶力学会议,南京,2009.
[2]田常录,胡 勇,刘道启,崔维成.深海耐压结构观察窗应力分析[J].船舶力学,2010,14(1-2):121-125.
[3]张志林.飞机座舱透明件设计理论及应用[D].南京:南京航空航天大学,2005.
Creep analysis on deep-sea structure’s viewport windows
TIAN Chang-lu1,HU Yong2,LIU Dao-qi3,CUI Wei-cheng2
(1 Jiangnan University,Wuxi 214122,China;2 China Ship Scientific Research Center,Wuxi 214082,China;3 Beijing Jiaotong University,Beijing 100044,China)
Human occupied sphere is the key component for deep-sea Human Occupied Vehicle(HOV).The difficulty of human occupied sphere design is the large openings such as human access opening and view windows opening.View windows usually are made of organic glass.In this paper,the stress,creep and boundary condition influences on windows of deep-sea HOV are analyzed by theoretical analysis and test.The theoretical calculation method is obtained.This paper can be used as a reference for such type of structure design.
deep-sea HOV;windows;creep,theoretical analysis
U674.941
A
1007-7294(2010)05-0526-07
2009-12-13
田常录(1963-),男,博士,江南大学机械学院教授,博士生导师,Email:cltian63@163.com。

