底层集合论

符国庆，方逵

（湖南农业大学信息科学技术学院，湖南 长沙 410128）

1 引言

有关集合，参考文献[1]中有如下论述：

“什么是集合？集合论的创始人Cantor曾作如下描述： ‘一个集合是我们直觉中或理智中，确定的，互不相同的事物的一个汇集，被设想为一个整体 （单位）’.这些事物叫做这个集合的元素，或者说这些元素属于这个集合，也说这集合包含这些元素.Cantor的描述对人们直观地理解集合概念是很有价值的.例如，它说一个集合的元素是 ‘确定的’，这意味着某个事物是否属于某个集合的元素是 ‘确定的’，某个事物是否属于某个集合是没有丝毫含混余地的；又如，它说一个集合的元素是 ‘互不相同的’，这意味着在一个集合中相同的元素只能算是一个；又如，它说把一个集合 ‘设想为一个整体 （单体）’，这意味着要把整个集合看成一个单独的思维对象，而不再看成那些个别元素的简单积累.现在有个问题需要说明：集合的元素是什么？我们的答复是集合的元素还是集合.例如：与一条已知直线平行的一切直线组成一个集合，这集合的元素是直线，而直线又可看成点的集合”.

[2]中针对集合却有如下一些论述：

“集合如同几何学中的点，线，面一样是数学里最基本的概念.我们不妨理解为所谓集合是由具有明确涵义的事物 （或个体）组成的集体.集合里的每一事物称为该集合的成员或元素.所谓事物，涵义也是广泛的，它可以是具体的东西，也可以是抽象的概念.经典集合的内涵和外延都是明确的，具有明确的内涵和外延的概念都可以用经典集合去表示.但是，日常生活中，也存在着像‘老年人’， ‘高个子’，等众多模糊概念.模糊概念是不能用经典集合来描述的，这里因为不能绝对的划分 ‘属于’与 ‘不属于’，只能说属于的程度是多少.那么怎样描述一个模糊概念呢？Zadeh[3]仿照用特征函数表示经典集合的方法，就是把特征函数的取值范围，从{0，1}的两个值扩大到 [0，1]闭区间内连续取值，即ΨA:U→ [0,1],(U为论域).Zadeh就是从这点取得突破，他利用经典集合这一工具，实现了定量地描述模糊集合.为了有所区别，我们特意将模糊集合的特征函数改称作 “隶属函数”.

对集合的论述，上述两种是目前使用最广、影响最大、也是普遍得以认可的典型代表，其它的有关集合论 （例如：可拓集合）一方面是：全盘承认上述两种后再拓展[4].另一方面是：论证了模糊集合论的缺陷与错误[5]，却对经典集合论的完善与扩充没有顾及.

2 问题的提出

首先不对Cantor的经典集合理论和Zadeh的模糊集合理论中存在的问题做任何论述，只是按现有的集合理论举一个前两本书都谈及的有关几何中点、线、面与集合关系的简单例子.

假设：论域U是一个建有以O为坐标原点，分别以X轴，Y轴，Z轴为标准正交直角坐标系的三个坐标轴的三维几何立体空间，试用集合的观点讨论平面XOY与U的关系.

当把U表示为所有与平面XOY垂直的直线构成的集合时，显然，不论按经典集合理论或模糊集合理论，论域中目前的元素是直线.如果按照Cantor的集合理论，因为平面XOY（可看成是过Y轴上的一点且与X轴平行的所有直线的集合）内任一条直线不可能与自身平面XOY垂直，所以平面XOY内的任一条直线都不可能是论域中的元素，照此，按经典集合理论中子集的定义(由元素与集合的关系说明的)，得出的结果是：平面XOY不可能是论域U的子集 （这一结果显然不能被现在的人所接受）.再按Zadeh的模糊集合理论，因为平面XOY在空间内，所以平面XOY是U的一个子集，不过不是经典子集，而是一个模糊子集.再根据Zadeh的集合理论，模糊子集只有靠隶属函数来描述，而与平面XOY垂直的所有直线 （即论域中每个元素）与平面XOY（即模糊子集）的隶属程度应该没有差别，试问这个隶属函数的函数值取多少会是合适呢？难道取不同的值就能给我们带来有关平面XOY的不同的信息吗？显然不能.这时谁还敢相信：由特征函数化名而来的隶属函数确实能全面反映平面XOY这一模糊子集 （暂时仍用这一名称）的本质呢.可见，虽然用模糊观点得到了人们希望的结果，但模糊理论的解释却无法让人信服.

然而，当再把论域表示为三维几何立体空间内所有的点构成的集合时，无论按Cantor集合理论还是Zadeh集合理论，结果都是一样，平面XOY集合是论域的一个经典子集.这不刚好是大家最希望看到的结果吗？

在用现有的集合理论解释客观世界的事物时，以上例子不仅揭露出了Cantor集合理论与Zadeh集合理论各自的欠缺，同时也给我们带来了新的启发.

第一 它告诉我们，在客观世界里，绝对不可再分的事物是不存在的.科学作为人类对客观世界的表达，在科学里与客观事物相对应的最适当的概念只有集合，元素只不过是集合的一种特殊形式，元素概念与集合概念不存在有本质的差别，是同一概念在不同场合扮演的不同角色.经典集合论中，虽有＂集合的元素还是集合＂的说法，但在同一论域里的元素与集合在具体操作中不能当成两个集合来直接运算 （例如：交、并、补），这是人为地割裂了它们之间的本质联系.

第二 人类在认识、表达客观世界以及解决客观世界里的实际问题时，同一论域可以有多种不同的表示形式，可以根据实际选择其中一种或者让多种形式并存.

因此，解决问题的关键在于根据面向对象的不同来合理划分我们的论域.不能人为割裂元素与集合的本质一致性，同一论域里的元素与集合之间的关系本质上仍是集合与集合的关系，完全可以进行直接运算.而且，同一论域里的元素与集合(本质上仍是集合与集合)的关系最合理的分法应是三种.而在经典集合论中元素与集合的关系只用了三种关系中的二种， 因为在实际应用中，经典集合论把元素与集合看成是本质不同的两个概念，并没有把 “不属于”定义为除 “属于”之外的所有情况，而是把 “不属于”的外延无意中限定在元素的全部应彻底在集合之外，并不认可元素与集合部分相交 (论文后会改称相粘连)的情况 （这种情况显然不是 “属于”关系，按概念的规范，可以称 “不属于”关系），这样，实际运用中的 “不属于”并没构成 “属于”的对立面.所以经典集合论只能很好地解决元素与集合确实只有二种关系的情况，当遇到存在有相交关系时，就只能置之不理.遗憾的是：模糊集合论虽然认可有第三种关系，却把问题模糊化、复杂化、甚至出现悖论[6]更不科学.

3 低层集合论

定义1 （也称集合公理）客观世界里一切确定的事物均可被抽象为低层集合 （为方便经典集合中＂集合＂名称能继续被正常使用，故另取它名，以示区别）.

约定1书写时， “{”表示从非低层集合概念进入低层集合的入口标记， “}”表示从低层集合出来进入非低层集合概念的出口标记.一个低层集合内的低层集合之间的分隔符有 “， （）”三个，而 “|”被书写在低层集合内时，表示注解.这些符号都不是集合本身的内容，仅当作分界标记或注解提示，除此之外，任何其它符号一般可以作为低层集合的标记.

约定2代表不含任何事物的低层集合被称之为空集，记作 {?} （或者 {}）.

关系公理：如果某一低层集合{A}的全部是另一低层集合{B}的一部分，则称{A}是{B}的低层子集，或称{B}包含{A}，记作{A}∈{B}或{A}c{B}.

约定3空集是任何低层集合的一个低层子集.

定义 2 如果{A}∈{B},同时{B}∈{A},则称{A}与{B}相等（或相同），记作{A}={B}.

定义3在同一标准要求下，对某一低层集合进行互斥划分，直接得到的所有低层集合均称之为预备元素，被当前采用的某次划分对应的预备元素，称之为当前元素.

（互斥：指任意两个低层集合之间，没有任何相等的非空低层子集）.

定义4能被现有的当前元素一个一个地直接表示出来的低层集合称之为当前可个体化集合，否则称当前不可个体化集合.（相对低层子集，也有相应的＂当前可个体化子集＂与＂当前不可个体化子集＂）.

定义5某低层集合，如果被当成是被讨论对象的全体时，该低层集合称之为论域或者全集.

定义6低层集合与低层集合之间 （当然包括低层集合与预备元素之间，预备元素与预备元素之间）有如下三种关系：

（1）如果{A}与{B}之间没有任何相等的非空低层子集，则称{A}与{B}相排斥（或称{A}相斥于{B}），记作{A}o{B}或{B}o{A}，（可简称{A}斥{B},＂o＂表示很容易分开，来源于＂open＂的首字母）.

（2）如果{A}是{B}的低层子集，则称{A}与{B}相包含，记作{A}∈{B}或{A}c{B}（{B}∈{A}意义类同），（可简称{B}含{A}或{A}含于{B}），＂c＂来源于＂Include＂的＂c＂.

（3）{A}与{B}之间除上述两种之外的其它所有情况，均称{A}与{B}相粘连，记作{A}v{B}（可简称{A}粘{B}或{B}粘{A}），＂v＂来源于快捷键＂ctrl＋v＂,表粘连.

定义7低层集合之间有如下运算：

（1）{A}∩{B}表示两者共同的某一低层子集，且该低层子集包含两者全部相同的低层子集，称之为{A}与{B}的交集.（多个或无数个也类同）.

（2）{A}∪{B}表示所有既包含{A}又包含{B}的低层集合的交集，称之为{A}与{B}的并集.

（3）{A}-{B}表示{A}的低层子集中所有与{B}相排斥的低层子集的并集，称之为{A}与{B}的差集.（显然{A}∈{B}时，{A}-{B}={?}）.

注意：没有把两个低层集合在同一论域表示形式下个体化 （即表成当前元素）时，运算结果可能只有含义，却不一定能写成当前可个体化集合的形式.

定理1： 空集是唯一的.

证明：假设还有一个空集 {Q}

根据关系公理与约定3

再根据定义2所以{?}={Q}

定理成立.

定理2：低层集合运算的基本定理： （证明与经典集合理论类同）

（1）幂等律，（2）结合律，（3）交换律，（4）分配律，（5）互补律（6）同一律，（7）零一律，（8）吸收律，（9）德.摩根律，（10）双重否定律.

附加说明：

（1）同一低层集合，根据需要，可以进行任意互斥划分.

（2）低层子集在运算中产生新低层集合时，仅作最简单的原始处理 （可允许赋予新低层集合相应的整体信息，但信息不是低层集合的本身内容，不进入低层集合的运算，这一点与经典集合思想不同）.

4 低层集合的表示

书写时,一般符号都可以当作低层集合的标记.对于当前不可个体化集合，无法借助当前元素来直接表示，只有靠语言描述.当前可个体化集合的表示方法仍可采用经典集合论的一些基本方法.

5 低层集合的应用举例

首先用上述低层集合的思想，回头解释前面三维几何空间与平面XOY关系的例子：

当论域被表示成所有与平面XOY垂直的直线构成的低层集合时，三维空间与平面XOY均是低层集合，且论域是整个三维空间.因为平面XOY的全部是空间的一部分，根据关系公理，这时平面XOY是论域的一个低层子集 （与论域是相包含的关系），当前元素是直线.由于能被当前元素直接表示的低层集合，至少含有一条与平面XOY垂直的直线 （一个当前元素），所以平面XOY现在是论域的一个当前不可个体化子集.论域与平面XOY的差集是 {除平面XOY之外的空间}，仍是一个当前不可个体化集合，它们的并集是论域 （当前可个体化集合）.当前元素Z轴与当前不可个体化集合平面XOY是相粘连的关系，它们的交集也是一个当前不可个体化集合.{Z轴的非坐标原点部分}是一个当前不可个体化集合，它与当前不可个体化集合平面XOY是相排斥的关系.

当论域被表示成 {（x y z）|x，y，z为实数}时，同样三维空间与平面XOY均是低层集合，论域是整个三维空间，平面XOY仍是论域的一个低层子集.不过，此时的当前元素是空间里所有的点 （或三维坐标），由于平面XOY能够被当前元素直接表示出来，所以平面XOY是论域的一个当前可个体化子集.论域与平面XOY的差集也是一个当前可个体化集合，它们的并集是论域（当前可个体化集合）.当前可个体化集合Z轴与平面XOY是相粘连的关系，它们的交集是一个当前元素 （坐标原点）.{Z轴的非坐标原点部分}是一个当前可个体化子集，它与平面XOY是相排斥的关系.

本例小结：

（1）不管论域被表示成什么形式，平面XOY总是论域的一个低层子集，不会有变化 （不再有二个固定的事物在一种表示形式下首先不是子集关系，换一种表示形式却成了子集关系的矛盾局面，修正了经典集合理论）.

（2）论域的某一表示形式下，平面XOY可能表现为当前不可个体化集合，但在另一种形式下，又有可能表现为当前可个体化集合 （并不模糊，修正了模糊集合理论）.

便于对照，不妨再看一个 “老年人”的例子：

设： 某单位成员有 A、B、C、D、E(20 岁)，F、G(60岁)，H(80 岁)共 8 人，另给函数 y=g（x）如下：

试讨论：该单位老年人员与单位所有人员的比值情况.

先按模糊集合理论来分析：设论域U为该单位所有人员集合，g（x）为该单位老年人集合对应的隶属函数，P(U)为U的幂集（包括所有U的模糊子集）.对于 P(U)中任一个元素 X，定 pos（X）等于 U中相应X特征函数的函数值是非零的元素的总个数除以总人数8.

根据参考文献[7]，不难验证：pos是 （U,P(U)）上的一个可能性测度，设：该单位全体老年人集合为L，则:

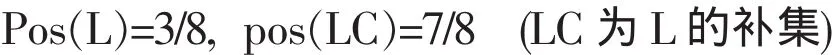
根据必要性测度的定义：Nec（L）=1-pos（LC）,则 Nec（L）=1/8

再根据可信性测度的定义：

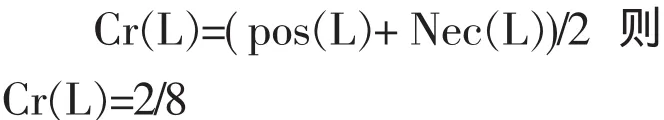
依模糊集合理论观点，2/8这个数在一定程度上反映了该单位老年人员与单位所有人员的比值情况.

再用低层集合理论来分析，把论域换一种表示形式.不妨把每一个人抽象地划分为＂老掉部分＂与＂年轻部分＂ （如同一个正在烤的红薯可以被抽象地划分为已烤熟部分与还没烤熟部分一样）.

{U}={（A 老， A 青）,（B 老， B 青）,（C 老， C青）,（D 老， D 青）, （E 老， E 青）, （F 老， F 青）,（G老， G青）,（H老，H青）}.

构造一个函数f（x）：自变量x为U中16个元素，函数 y=f（x）如下：

（其实，构造的函数还可以更详细，因为同样是60岁的人，他们老掉的部分可能会不一样）.

设：本例中当前可个体化集合的总量为低层集合内所有当前元素对应的f（x）函数值的总和.则

老年人集合 {A老，B老,C老，D老，E老，F老，G老，H老}的总量为：

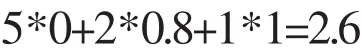
论域的总量为：

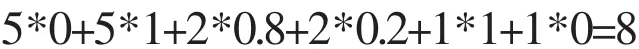
如果我们用老年人集合的总量与论域的总量之比来反映该单位老年人员与单位所有人员的比值情况，这个比值就是2.6/8.

比较2/8与2.6/8这二个数，不难发现：这个单位8个人中有近2.6个老年人是合理的,既直观，又具说服力.

为进一步加深对低层集合论的认识，再谈谈举世有名的罗素悖论的问题.

Russell(1872-1970)曾把集合分成两大类：第一类：如果集合A是集合A的一个元素,称A为第一类集合.第二类：如果A集合不是集合A的一个元素，称A为第二类集合.设Q为所有第二类的集合所组成的集合，那么，Q是第一类集合呢?还是第二类的集合呢?这就是举世有名的罗素悖论问题.

在经典集合论中，依靠元素来说明或描述集合，而且，在一般定义里是否允许用一个还待说明的事物来说明另一事物，当初没有明确的回答.如果允许，就无法回答罗素的问题，如果不允许，则最早可用于说明其它事物的概念从哪儿来呢，现在大家已知道，这时应用公理化的思想，只有在公理里才允许用没有定义的概念出现，一般情况是不能使用的.但最初人们却没有明确公理化的思想，对罗素的问题也不能有一个清晰的交待.有了公理化思想之后，现在的人才能庆幸用公理化思想，可以说服罗素.不过在此，低层集合论却要给出说服罗素的另一更简单的方法--只要让罗素知道低层集合的思想与方法，这样他根本就不会提这样的问题，因为：

第一任何低层集合 ｛A｝都是自身 ｛A｝的一个低层子集 （包括空集），如果把非空低层集合 ｛A｝当成是集合 ｛A｝的一个当前元素，则根据定义3，另一个当前元素只能是 ｛?｝，可表示为： {A}={A，?} （空集时， {?}={?}）.所以任一个低层集合在一定条件下，都能表示出是自身的一个当前元素.＂集合A是集合A的一个元素＂，在一定意义上，一切低层集合都是这样，经典集合论中元素A与集合 {A}在低层集合论中不再有本质的差别.

第二罗素悖论中说的第二类集合，在低层集合论中，只算是不把集合 {A}当成 {A}的一个当前元素的条件下，众多低层集合的表现形式中的一种表现， 例如： 当定 {A}={1，2，3，4}时， 按经典集合论的观点看，等式右边4个元素中没有集合A，称得上是第二类.但在低层集合论中，当把低层集合{A}当成{A}的一个当前元素的条件下，{A}也可表示成：{（1，2，3，4），（?）}，此时低层集合{A}仍可以说是自身的一个当前元素.

第三罗素悖论问题其实质是要经典集合论按集合与元素本质分开的方式来回答集合A与集合A的元素的关系问题，当然只有矛盾的结果.如果按低层集合论，因为把经典集合论中的元素与集合本质上统一了，结果是：任一个低层集合在一定条件下，都能表示出是自身的一个当前元素，但一个低层集合也可以表成当前元素中没有低层集合自身式样的形式.这样在低层集合论里，如果还按低层集合 ｛A｝是不是低层集合 ｛A｝的一个元素来分类，不再具有任何分类的意义.到此，聪明的罗素怎么还会愿意提这样的问题呢？

6 结论

低层集合理论兼容了经典集合的绝大部分内容.例如：在经典集合理论中， “集合”就是低层集合理论中的 “当前可个体化集合”.“子集”是低层集合理论中的 “当前可个体化子集”.“元素”就是低层集合理论中的＂当前元素＂等等.

针对模糊集合理论里多数内容缺乏直观性与有效性，低层集合理论只借鉴了其中极少部分内容.

低层集合理论提出了一种全新的集合思想.认为：客观世界里一切确定的事物均可被抽象为低层集合.尤其强调：预备元素与低层集合一样，可以被划分为更小部分，本质上预备元素与低层集合没有差别，它们之间可分为相排斥、相包含、相粘连三种关系.在实践中,低层集合理论比现有集合理论更能广泛地反映客观世界一切确定的事物.

参考文献:

[1]董延闿.基础集合论[M].北京：北京师范大学出版社，1988:11.

[2]肖位枢.模糊数学基础及应用[M].北京：航空工业出版社，1992.

[3]Zadeh L A.Fuzzy sets[J].InfSci，1965(8)：338-353.

[4]王汝发 .从“集合”的由来演化看数学哲学的基本问题[J].湖南大学学报：社会科学版，2003,17（2）：61-64.

[5]高庆狮.Zadeh模糊集合理论的缺陷及其改进:C*--糊集合理论[J].北京科技大学学报,2005,27(5):513-519.

[6]Elkan C.The paradoxical success of fuzzy logic[J].IEEE Expert,1994,9(4):3-8.

[7]刘宝碇，赵瑞清，王 纲，等 .不确定规划及应用[M].北京：清华大学出版社，2003:8.