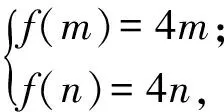“3个二次”的命题趋势、题型与策略

● (学军中学 浙江杭州 310012)

在高中数学中，“3个二次”是以二次函数为中心，运用二次函数的图像、性质把其余“2个二次”串联起来，构成知识系统的网络结构，而且这“3个二次”也是研究其他内容的基础工具.高考对“3个二次”的考查往往渗透在其他知识的考查之中，并且大都出现在解答题之中，特别是与不等式、导数以及解析几何等高中数学的主干知识的结合成为其一大亮点.其考查的重点是二次函数的图像与最值、一元二次方程以及根的分布等内容.在2009年全国新课程高考数学的理科试卷中，每套均含有有关“3个二次”的试题.

1 命题趋势

二次函数与二次方程、二次不等式的交汇自然贴切、一脉相承，纵观历年的高考试题，以“3个二次”为纽带编制而成的综合题立意新颖、灵活性强，对各种能力和思想方法都提出了很高的要求.2010年高考命题的趋势主要表现在：(1)与二次函数的图像、性质有关的选择题、填空题；(2)以二次方程的根的分布、在限定区间上的二次函数的最值、含参数的二次不等式恒成立、二次不等式的解法、二次方程的解法为基点与其他知识的交汇，尤其是与三角函数、导数、解析几何的交汇问题.

2 题型与策略

题型1二次函数的性质问题

解决有关二次函数的性质问题，关键是熟悉二次函数的图像、定义域、值域、对称性、单调性、奇偶性等.

( )

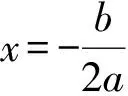
A.{1,2} B.{1,4}

C.{1,2,3,4} D.{1,4,16,64}

(2009年福建省数学高考理科试题)

分析利用换元法，设f(x)=y，原方程化为my2+ny+p=0,根据此一元二次方程的根的情况与二次函数f(x)的图像的对称性进行分析.

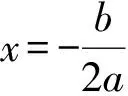
题型2限定区间上的二次函数最值(值域)问题

求限定区间上的二次函数的最值(值域)问题，要看开口方向以及对称轴在该区间的相对位置，即对称轴在区间的左侧、右侧、区间内，因而引起分类讨论.二次函数在闭区间上必存在最大值和最小值，它们分别在区间端点或顶点处取得.

例2已知二次函数f(x)=-x2+2x，是否存在实数m,n(m

分析这是限定区间上的二次函数的值域(最值)问题，按常见思路需要分类讨论;若根据二次函数f(x)在[m,n]上的值域是二次函数f(x)在R上的值域的子集，则可以避免分类讨论.

解假设满足题设条件的m,n存在.因为

f(x)=-(x-1)2+1≤1,

所以

[4m,4n]⊆(-∞,1]，

即

解得

又m

题型3一元二次方程的根的分布问题

解决这类问题有2种基本策略：一是利用韦达定理，如一元二次方程ax2+bx+c=0在(1,+∞)上有2个不等的实根,等价于

二是利用二次函数的图像，譬如一元二次方程ax2+bc+c=0(a>0)在(1,+∞)上有2个不等的实根,等价于

其中f(x)=ax2+bx+c.

例3已知函数f(x)=|x2-1|+x2+kx.

(1)若k=2，求方程f(x)=0的解;

分析根据绝对值的意义，将含有绝对值的方程化为一元二次方程或一元一次方程.

解(1)当x2-1≥0,即x≤-1或x≥1时，2x2+2x-1=0,解得

因为方程1+kx=0在(0,1]上至多有1个实根，方程2x2+kx-1=0在(1,2)上至多有1个实根，结合已知，可得方程f(x)=0在(0,2)上的2个解x1,x2中的1个解在(0,1]上，1个解在(1,2)上，不妨设x1∈(0,1],x2∈(1,2).由f(x)=0,得

作出函数

图1

的图像，如图1所示.因此

且

故

评注在第(2)小题中，利用了“若ac<0，则一元二次方程ax2+bx+c=0有2个异号的实根”，从而确定x1,x2所在的范围.

题型4含参数一元二次不等式恒成立问题

含参数的一元二次不等式在限定区间上恒成立的问题可以转化为在限定区间上的二次函数的最值问题或一元二次方程的根的分布问题,有如下的结论：

设f(x)=ax2+bx+c(a>0)，则

(1)求函数f(x)的极大值；

(2)若当x∈[1-a,1+a]时，恒有-a≤f′(x)≤a成立(其中f′(x)是函数f(x)的导函数)，试确定实数a的取值范围.

分析第(2)小题就是含参数的一元二次不等式在x∈[1-a,1+a]上恒成立，求参数的范围问题.

解(1)f′(x)= -x2+4ax-3a2=

-(x-a)(x-3a).

令f′(x)=0，解得

x=a或x=3a.

当x∈(-∞,a)或x∈(3a+∞)时,f′(x)<0;当x∈(a,3a)时，f′(x)>0.因此f(x)在(-∞,a)上单调递减，在(a,3a)上单调递增，在(3a,+∞)上单调递减，于是函数f(x)的极大值为f(3a)=1.

(2)由已知得,-a≤-x2+4ax-3a2≤a在x∈[1-a,1+a]时恒成立.

①由-x2+4ax-3a2≥-a,可得x2-4ax+3a2-a≤0在x∈[1-a,1+a]时恒成立.设g(x)=x2-4ax+3a2-a,则

即

解得

②由-x2+4ax-3a2≤a,得x2-4ax+3a2+a≥0在x∈[1-a,1+a]时恒成立.因为0

Δ=16a2-4(3a2+a)=4a(a-1)<0，

因此x2-4ax+3a2+a≥0在x∈[1-a,1+a]时恒成立.

评注第(2)小题在处理x2-4ax+3a2+a≥0在x∈[1-a,1+a]时恒成立时，注意到Δ<0，从而简化了运算.

题型5含参数的一元二次不等式有解问题

根据特称命题的否定是全称命题，将含参数的一元二次不等式有实数解的问题转化为含参数的一元二次不等式恒成立的问题.

例5已知函数f(x)=x2,g(x)=x-1．若存在x∈R,使得f(x)

分析含参数的一元二次不等式f(x)

解先求使不等式f(x)≥b·g(x)，即x2-bx+b≥0对任意x∈R都成立时实数b的取值范围.由Δ=b2-4b≤0,解得

0≤b≤4.

因此，所求的实数b的取值范围是b<0或b>4.

评注解决本例也可直接利用二次函数的图像，得Δ=b2-4b>0,解得b<0或b>4.

精题集粹

1．已知二次函数f(x)=x2+2(p-2)x+p，若在区间[0,1]内至少存在1个实数c，使得f(c)>0，则实数p的取值范围是

( )

A．(1,4) B．(1，+∞)

C．(0，+∞) D．(0，1)

2．已知方程ax2+bx-1=0(a,b∈R且a>0)有2个不等的实根，其中1个根在区间(1,2)内，则a-b的取值范围为

( )

A．(-1,+∞) B．(-∞,-1)

C．(-∞,1) D．(-1，1)

3．已知函数f(x)=2x2+(4-m)x+4-m，g(x)=mx,若对于任一实数x，f(x)与g(x)至少有1个为正数，则实数m的取值范围是

( )

A．[-4,4] B．(-4，4)

C．(-∞,4) D．(-∞,-4)

4．已知关于x的方程4x-2x+1+3m-1=0有2个实根，则m的取值范围________.

5．已知3x2+2y2-6x=0,则z=x2+y2的最大值为________.

6．关于x的方程(x2-1)2-|x2-1|+k=0，给出下列4个命题：

①存在实数k，使得方程恰有2个不同的实根；②存在实数k，使得方程恰有4个不同的实根；③存在实数k，使得方程恰有5个不同的实根；④存在实数k，使得方程恰有8个不同的实根.

其中真命题的是________．

(2)若函数f(x)的递增区间为[s,t]，求|s-t|的取值范围.

8．已知f(x)=ax3+bx2+cx+d是定义在R上的函数，其图像交x轴于点A，B，C.若点B的坐标为(2，0)，且f(x)在[-1，0]和[4，5]上有相同的单调性，在[0，2]和[4，5]上有相反的单调性.

(2)在函数f(x)的图像上是否存在一点M(x0,y0)，使得f(x)在点M的切线斜率为3b？若存在，求出点M的坐标；若不存在，请说明理由.

(3)求|AC|的取值范围.

参考答案

1．C 2．B 3．C

(2)|s-t|的取值范围为[2,4).