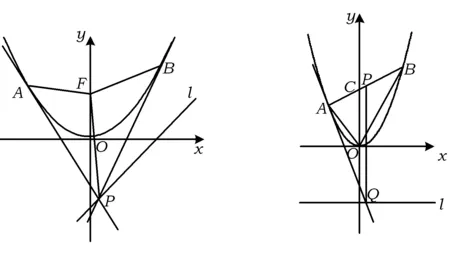
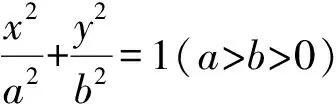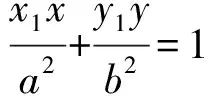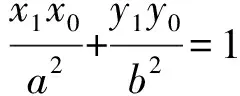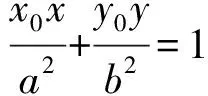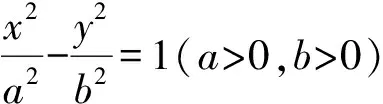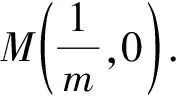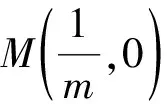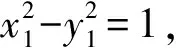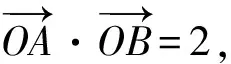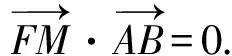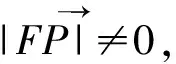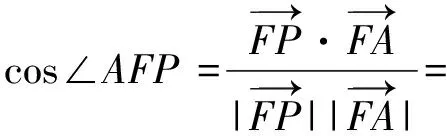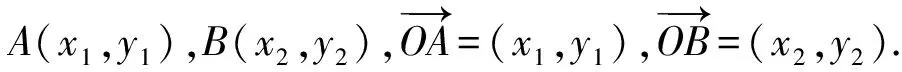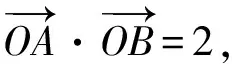圆锥曲线切线方程的探索
● (杭州外国语学校 浙江杭州 310023)
纵观近几年的高考试卷,发现圆锥曲线以切线为背景的问题经常出现在各地的高考试题中.这类问题往往因为运算量大而且计算十分复杂,最终被考生因为时间不够而放弃.为此,本文结合高考实例探索圆锥曲线切线方程的求法,以供参考.
1 利用判别式求切线
用判别式求切线是常规的方法,即把直线方程和圆锥曲线方程联立,通过消元得到一元二次方程,然后用判别式求解.但这种方法往往运算量较大.
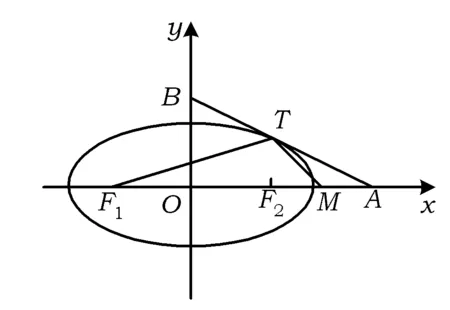
图1
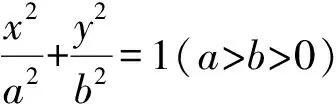
(2006年浙江省数学高考试题)
分析因为直线和椭圆相切,所以直线和椭圆联立,通过判别式来解决.
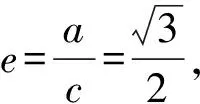
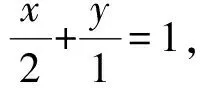
于是联立方程组
整理得
即
x2-2x+2-2b2=0.
又因为直线AB和椭圆相切,所以
Δ=4-4(2-2b2)=0,
解得
2 利用导数求切线
导数进入新教材之后,给直线和圆锥曲线的相切注入了生机和活力,开辟了解题新途径,这样可以避开联立方程组的繁琐运算.
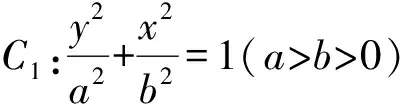
(1)求椭圆C1的方程.
(2)设点P在抛物线C2:y=x2+h(h∈R)上,C2在点P处的切线与C1交于点M,N.当线段AP中点与MN中点的横坐标相等时,求h的最小值.
(2009年浙江省数学高考试题)
解(1)由题意得
解得
a=2,b=1,
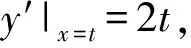
4x2+(2tx-t2+h)2-4=0,
即 4(1+t2)x2-4t(t2-h)x+(t2-h)2-4=0.
因为直线MN与椭圆C1有2个不同的交点,所以
Δ1=16[-t4+2(h+2)t2-h2+4]>0.
设线段MN中点的横坐标是x3,则
设线段PA中点的横坐标是x4,则
由题意得x3=x4,即
t2+(1+h)t+1=0,
其中
Δ2=(1+h)2-4≥0,
解得
h≥1或h≤-3.
当h≤-3时,有
h+2<0,4-h2<0,
不等式
Δt=16[-t4+2(h+2)t2-h2+4]>0
不成立,从而h≥1.
当h=1时,代入方程
t2+(1+h)t+1=0
解得t=-1.将h=1,t=-1代入不等式
Δt=16[-t2+2(h+2)t2-h2+4]>0
成立.因此h的最小值为1.
3 利用公式求切线
利用隐函数求导可以得到圆锥曲线在点P处的切线方程,有以下结论:
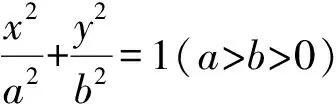
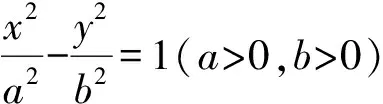
结论3过抛物线y2=2px上一点P(x0,y0)的切线方程为y0y=p(x0+x).
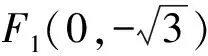
(2006年全国数学高考试题Ⅰ)
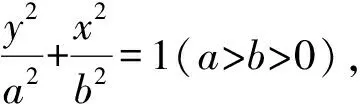
根据题意设A(x,0),B(0,y),P(x0,y0),则M(x,y),曲线C在点P处的切线方程为
即
得
又因为点P在曲线C上,所以
因为
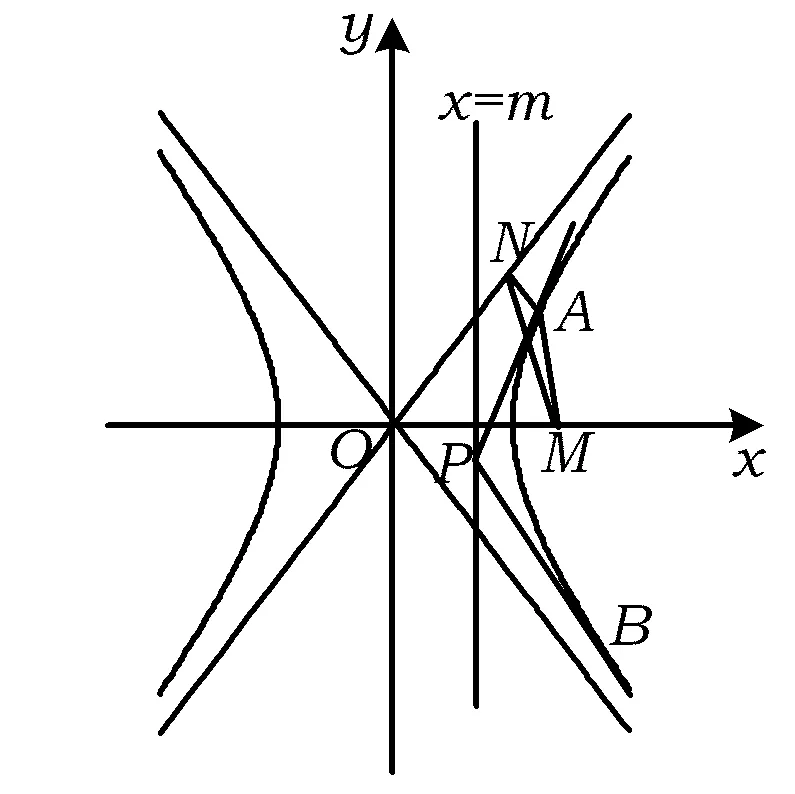
0 则 x>1,y>2, 所以点M的轨迹方程为 在近几年的高考试题中,有很多切线问题都涉及到切点弦,利用切点弦的知识可以轻松地解决一些试题.下面的结论在解题中经常用到. 证明利用结论1,得经过切点P1(x1,y1),P2(x2,y2)的切线方程为 因为它们都经过点P(x0,y0),所以 结论6经过抛物线y2=2px外一点P(x0,y0)引抛物线的2条切线PP1和PP2,其中P1(x1,y1),P2(x2,y2)为2个切点,则经过P1,P2的直线方程为y0y=p(x0+x). 我们发现切点弦方程和圆锥曲线上一点的切线方程在形式上完全一样,区别在于点P的位置不同. (1)求证:点A,M,B共线. (2)过点M作直线x-y=0的垂线,垂足为N,试求△AMN的重心G所在的曲线方程. (2008年江西省数学高考试题) (1)证明考虑应用切点弦方程,如图2,过P(x0,y0)作双曲线x2-y2=1的2条切线PA,PB,则过点A,B的切点弦方程为 x0x-y0y=1. 图2 又因为点P在直线x=m(y≠±m,0 mx-y0y=1. (2)解垂线AN的方程为 y-y1=-x+x1. 由 得垂足 设重心G(x,y),则 解得 即 为重心G所在的曲线方程. 精题集粹 ( ) (2009年全国数学高考理科试题Ⅰ) 2.过定点P(1,4)作直线交抛物线C:y=2x2于点A,B,过点A,B分别作抛物线C的切线交于点M,则点M的轨迹方程为________. (2)设△ABM的面积为S,写出S=f(λ)的表达式,并求出S的最小值. (2006年全国数学高考试题Ⅱ) 5.如图3,设抛物线C:y=x2的焦点为F,动点P在直线l:x-y-2=0上运动,过点P作抛物线C的2条切线PA,PB,且与抛物线C分别相切于点A,B. (1)求△APB的重心G的轨迹方程; (2)证明:∠PFA=∠PFB. 图3 图4 6.如图4,在平面直角坐标系xOy中,过y轴正方向上一点C(0,c)任作一直线,与抛物线y=x2相交于点A,B,一条垂直于x轴的直线分别与线段AB和直线l:y=-c交于点P,Q, (2)若P为线段AB的中点,求证:QA为此抛物线的切线; (3)试问第(2)小题的逆命题是否成立?说明理由. 参考答案 1.C 2.y=4x-4 3.4 4.(1)证明设M(x0,y0),得F(0,1),则切点弦AB的方程为 x0x=2(y0+y). 由条件知点F在直线上,因此y0=-1,从而 又直线AB的方向向量为(2,x0),所以 (2)解由第(1)小题知,切点弦AB的方程为 x0x=2(y-1), 即 与抛物线联立方程组得 x2-2x0x-4=0, 于是 又由MF⊥AB,得 从而 因此当x0=0时,面积最小,最小值为4.此时点A,B被点F平分,故λ=1. 5.(1)解利用切点弦方程可得 (2)证明由题意得 由点P在抛物线外,得 同理可得 因此 ∠PFA=∠PFB. 6.(1)解设过点C的直线为y=kx+c,则 x2=kx+c(c>0), 即 x2-kx-c=0. 所以 x1x2+y1y2=2, 即 x1x2+(kx1+c)(kx2+c)=2. 于是 x1x2+k2x1x2-kc(x1+x2)+c2=2, 整理得 c2-c-2=0, 解得 c=2或c=-1(舍去). (2)证明设过点Q的切线为 y-y1=k1(x-x1), 由题意得y′=2x,因此k1=2x1,即 所以点M和点Q重合,也就是QA为此抛物线的切线. 所以P为AB的中点.4 利用切点弦求切线