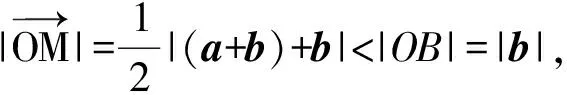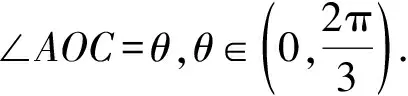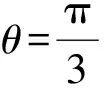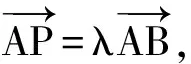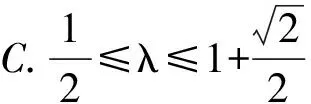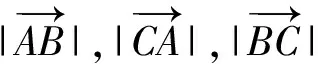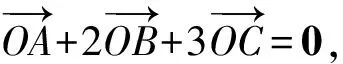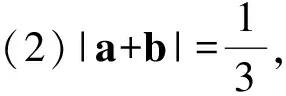平面向量题型和高考走势
● (杭州市第十四中学 浙江杭州 310006)
1 考点回顾
平面向量是高中数学的三大数学工具之一,同时具有代数的运算性和几何的直观性.向量是数形结合的典范,是高考命题的基本素材和主要背景之一,也是近几年高考的热点.准确把握平面向量的概念与运算,正确理解向量的几何意义,充分发挥图形的直观作用,这样才能较好地解决这类问题.常见的考点有:
(1)平面向量的基本概念、向量的加法与减法;
(2)共线向量的充要条件、向量的基本定理和坐标表示;
(3)实数与向量的积、向量的数量积与运算律;
(4)向量与平面几何、向量和其他问题的整合等.
重点是:向量的几何意义、共线向量、向量基本定理、向量的数量积、坐标运算、向量的平行和垂直、夹角、模长.
2 命题趋势
纵观近几年的考题,强调了试题的几何背景,特别是浙江省的高考试题,无不凸现了试题的几何背景,当然命题者也兼顾了向量的代数性质,因此解题的主要手段从以传统的计算为主转变为以挖掘问题的几何背景为主.
3 典例剖析
题型1以向量的基本概念为载体
这类问题主要考查学生对向量基本概念的理解,以简单概念辨析和简单计算为主.
例1已知a,b的夹角为120°,|a|=1,|b|=3,则|5a-b|=________.
(2008年江苏省数学高考试题)
分析关于向量模长的计算一般可利用公式|a|2=a·a解决.
解因为
|5a-b|= (5a-b)2=
25a2-10a·b+b2=
49,
所以
|5a-b|=7.
评注本题主要考查向量的线性运算,其难点是向量模长的计算,解决这类问题的基本方法是先求模长的平方.
题型2以向量的基本运算为载体
这类问题往往是代数问题,但多与不等式、几何图形相结合,代数形式的背后往往隐藏着美丽的几何图形.
例2已知a,b是平面内2个互相垂直的单位向量,若向量c满足(a-c)·(b-c)=0,则|c|的最大值是
( )
(2008年浙江省数学高考试题)
分析第1种思路是把向量坐标化;第2种思路是转化式子(a-c)·(b-c)=0;第3种思路是挖掘式子(a-c)·(b-c)=0的几何意义.
解法1不妨设a=(1,0),b=(0,1),c=(x,y).由(a-c)·(b-c)=0,得
(1-x,1-y)·(-x,1-y)=0,
即
故
解法2因为|a|=|b|=1,a·b=0,所以展开(a-c)·(b-c)=0,得
|c|2=c·(a+b)=|c|·|a+b|cosθ,
即
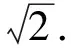
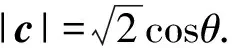

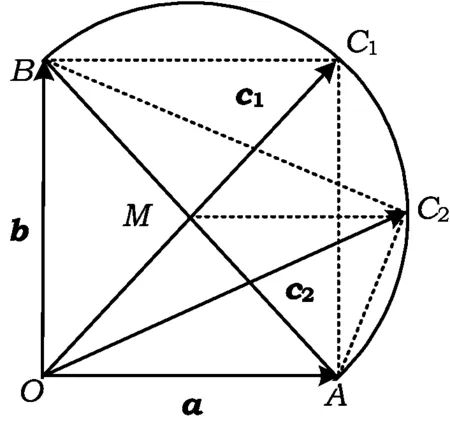
图1
连结AB,以AB为直径作半圆M,在半圆M上的任何一点C2,都满足∠AC2B=90°,也即符合条件
(a-c2)·(b-c2)=0.
再连结MC2,那么
|OC2|≤ |OM|+|MC2|=
|OC1|,

即
该解法既充分利用了向量的特点,又着意发挥了几何的优势,真是向量几何,珠联璧合啊!
题型3以向量基本定理为载体

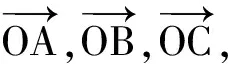
分析理解向量基本定理中参数λ,μ的含义,其实际意义就是向量在斜坐标中的坐标.
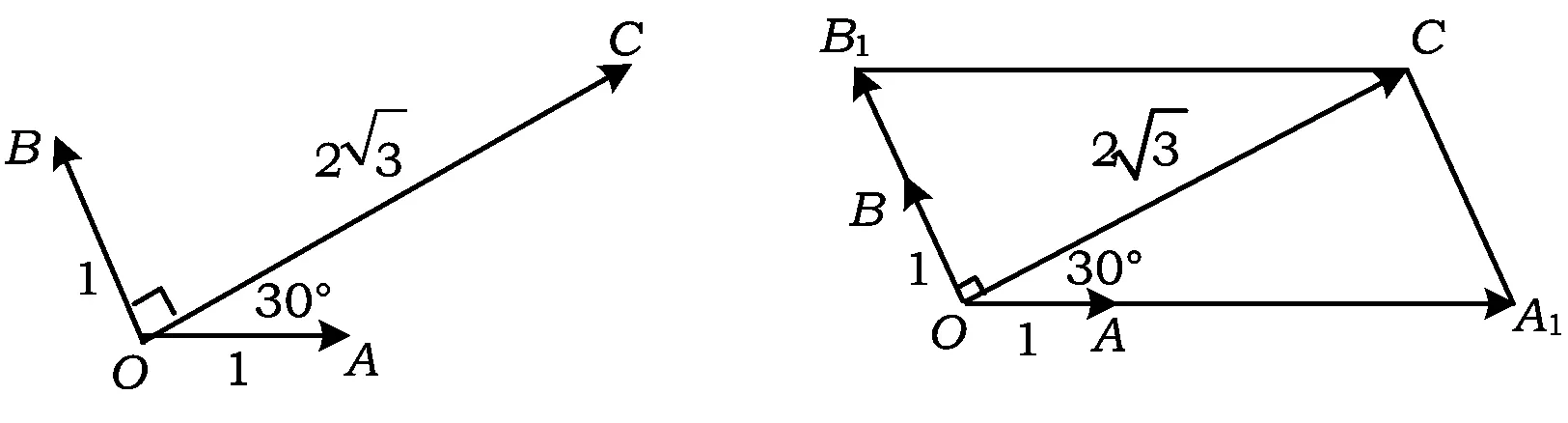
图2 图3
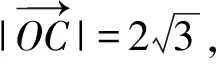
在Rt△B1OC中,因为∠OCB1=30°,所以
于是
即
λ+μ=6.
评注本小题主要考查向量的基本定理,理解向量基本定理中λ,μ的几何意义.本题的解答充分利用原图中既有直角,又有30°角的特征,从而构造含30°角的直角三角形.
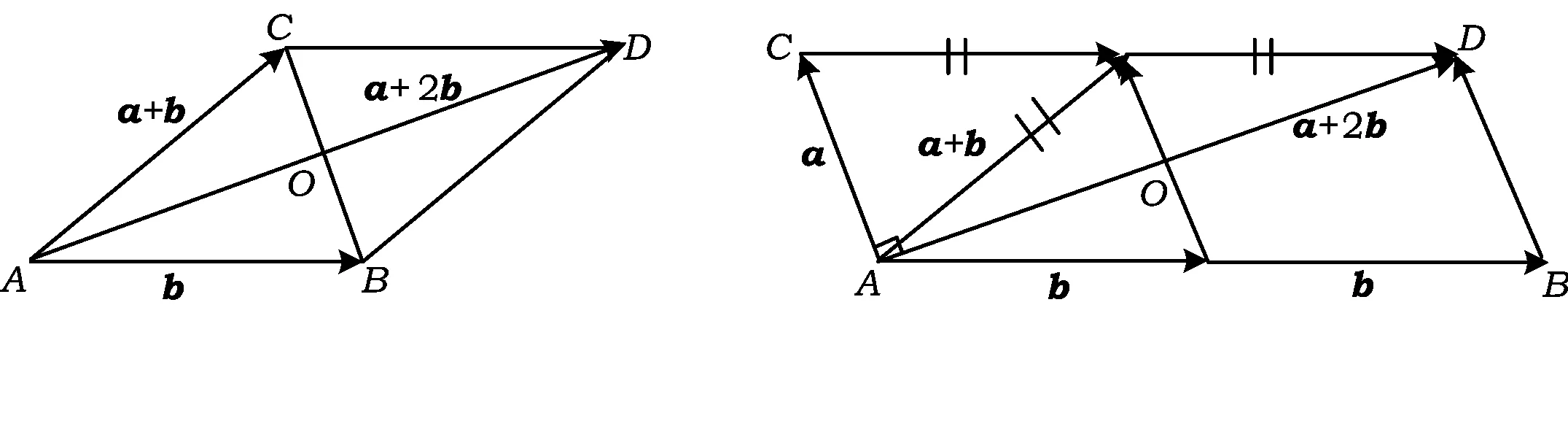
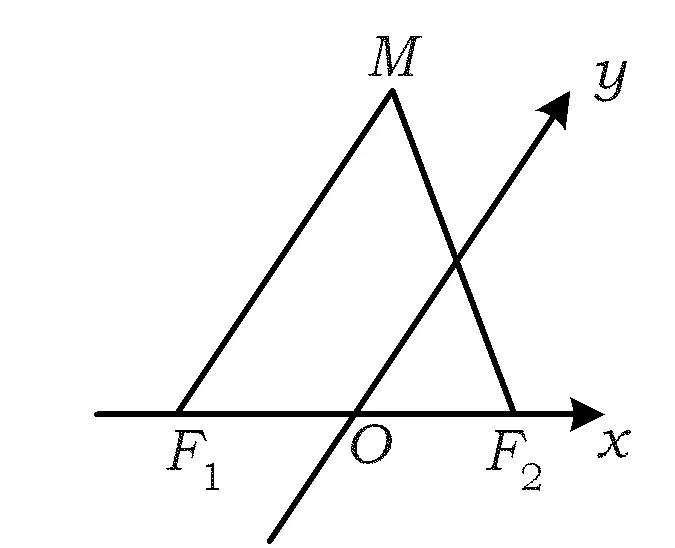
题型4以平面几何问题为载体
这类问题一般有2种解题思路:一种是利用三点共线的充要条件列方程;另一种是直接利用平面几何知识解决.

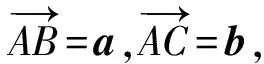
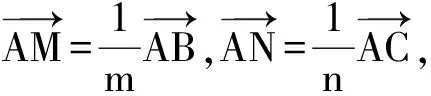
由向量相等的定义知
消去λ得
m+n=2.
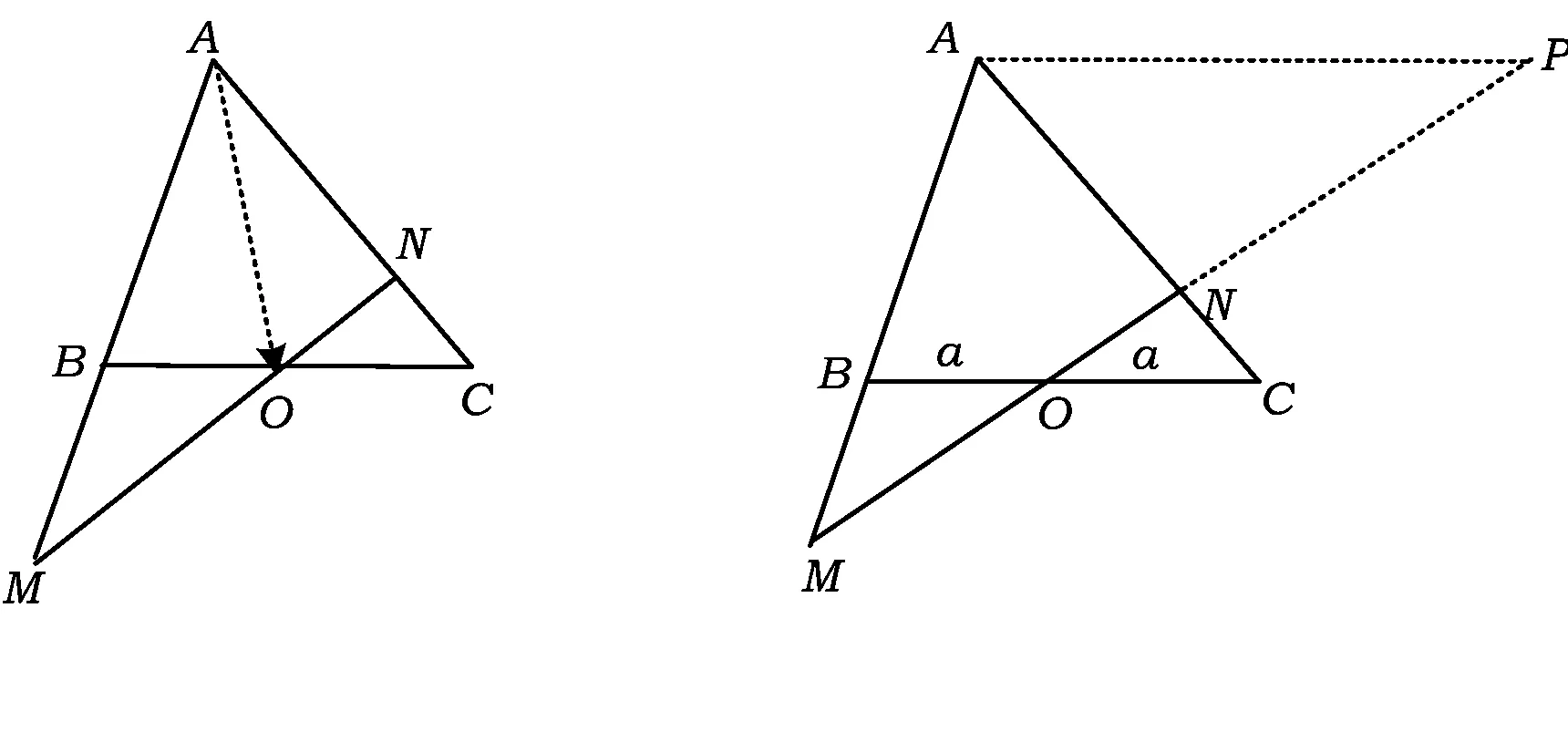
图4 图5
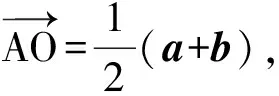
求解这类问题的关键是利用好图形中的三点共线.本题也可以利用平面几何知识求解:
即
因为△MOB∽△MPA,所以
同理可得
又由△CON∽△ANP,得
于是
1-m=n-1,
解得
m+n=2.
本题的条件比较分散,解题的关键是作平行线AP,通过2组相似三角形的联接与过渡,巧妙地解决了问题.
题型5以问题的几何背景为载体
自浙江省自主命题以来,向量问题常考常新.虽然问题年年翻新,但都富有内涵——深刻的几何背景,每一个代数形式的背后都有美妙的几何图形,解决这类问题的最佳办法是探寻问题的代数结构背后的几何结构.
例5(1)已知a≠e且|e|=1,若对任何实数t均有|a-te|≥|a-e|成立,则
( )
A.a·e=0 B.a⊥(a-e)
C.c⊥(a-e) D.(a-e)⊥(a+e)
(2005年浙江省数学高考试题)
(2)已知a,b是2个相互垂直的单位向量,而|c|=13,c·a=13,c·b=4,则对于任意实数t1,t2,|c-t1a-t2b|的最小值是
( )
A.5 B.7 C.12 D.13
(2005年浙江省高中数学竞赛试题)
(3)若非零向量a,b满足|a+b|=|b|,则
( )
A.|2a|>|2a+b| B.|2a|<|2a+b|
C.|2b|>|a+2b| D.|2b|<|a+2b|
(2007年浙江省数学高考试题)
解(1)构造图6可以判断当且仅当e⊥(a-e)时,有|a-te|≥|a-e|.
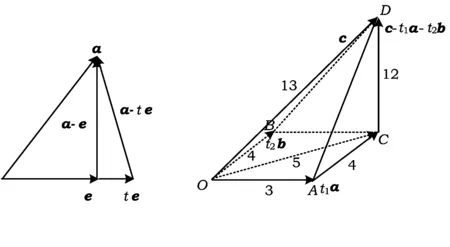
图6 图7
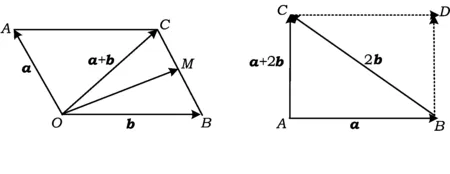
(3)背景1向量加法的平行四边形法则
解法1因为|a+b|=|b|,即AC=AB,所以四边形ABCD为菱形,如图8,因此AO 即 |a+2b|<|2b|. 解法2如图9,△ADC是直角三角形,因此AD 图8 图9 背景2三角形中线向量的表达式 即 |a+2b|<2|b|. 背景3三角形不等式 ||a|-|b||≤|a+b|≤|a|+|b|. 解法4|a+2b|≤ |(a+b)+b|≤ |(a+b)|+|b|=2|b|. 图10 图11 背景4向量垂直的充要条件 已知a,b为非零向量,求证: a⊥b⟺(a+b)=(a-b). 解法5由|a+b|=|b|,得 |2(a+b)|=|2b|, 因此 |(a+2b)+a|=|(a+2b)-a|, 即 2a+2b⊥a, 故可构造如图11所示的矩形,结论显然成立. 评注本题主要考查学生对向量的代数和几何结构之间的转化,如何充分挖掘向量的代数运算和几何性质之间的关系是掌握向量数学本质的关键. 题型6以平面直角坐标系为载体 (2009年安徽省数学高考试题) 图12 图13 即 解得 评注尽管本题的解法很多,但这个解法直观,容易被大多数学生接受和理解. 精题集粹 1.连续掷骰子2次分别得点数m,n,则a=(m,n)与b=(-1,1)的夹角θ>90°的概率是 ( ) ( ) ( ) A.反向平行 B.同向平行 C.互相垂直 D.既不平行也不垂直 4.已知平面向量a=(2,4),b=(-1,2).若c=a-(a·b)b,则|c|=________. 5.已知点A,B,C不共线,且有 图14 (1)求证:(a-b)⊥(a+b); 参考答案 1.D 2.B 3.A 8.(1)(a-b)·(a+b)=a2-b2=0