钻孔与冲击对碳/环氧复合材料电阻影响的计算模型

谢小林, 权红英, 李志鹏, 王高潮, 张建超

(1.武汉理工大学材料科学与工程学院,武汉 430070;2.南昌航空大学无损检测技术教育部重点实验室,南昌 330063）

钻孔与冲击对碳/环氧复合材料电阻影响的计算模型

谢小林1,2, 权红英2, 李志鹏2, 王高潮2, 张建超2

(1.武汉理工大学材料科学与工程学院,武汉 430070;2.南昌航空大学无损检测技术教育部重点实验室,南昌 330063）

分别对碳/环氧复合材料进行钻孔和冲击,并测量了钻孔或冲击前后复合材料的电阻,分析了材料电阻变化的机理,建立了复合材料电阻变化计算模型。结果表明,钻孔与冲击都会使复合材料中碳纤维之间接触点(电流截面积）及电荷传导路线发生变化,从而引起复合材料电阻变化。由钻孔对复合材料电阻影响的计算模型推导的冲击计算模型,能够极大地简化有关冲击对复合材料的影响的计算。根据本文所建立的计算模型可以计算出钻孔与冲击引起的复合材料电阻变化率,且与实验测量值相吻合。

碳/环氧复合材料;钻孔;冲击;电阻变化;计算模型

由于碳纤维具有良好导电性,有较高碳纤维含量(碳纤维含量为 65%～75%）的碳 /环氧复合材料通过碳纤维之间的相互接触形成导电网络而能够导电。复合材料的导电性能与自身内部结构、纤维含量、外力作用、温度等因素密切相关。任何改变碳纤维之间接触状态的因素都会影响复合材料的电阻值,因此,可以利用复合材料电阻值的变化对其内部结构的变化进行自诊断。有不少研究者利用碳纤维增强复合材料本身的导电性能,并把它作为材料力学、电学性能传感器对复合材料进行了研究[1～6]。也有人研究了碳/环氧复合材料微观导电模型以及温度、应力对复合材料电阻变化模型,表明复合材料的导电与碳纤维直径、碳纤维之间接触状况及接触点数量等有关[7～9],但难以准确测量影响条件、计算复合材料宏观电阻变化情况。

钻孔是复合材料在制造或装配过程中经常遇到的情况。冲击是碳/环氧复合材料在使用过程中较常见的外力作用形式,较大能量的冲击会使碳/环氧复合材料产生分层或穿孔损伤。钻孔和冲击损伤都会破坏碳/环氧复合材料中碳纤维的导电网络,从而引起复合材料电阻的变化。本文测试了冲击或钻孔前后碳/环氧复合材料电阻变化,分析了复合材料电阻变化的原因,建立了复合材料电阻变化计算模型,为研究基于电阻法自诊断碳/环氧复合材料提供依据。

1 实验

1.1 原材料和主要设备

原材料采用商品级的 G803/5224碳纤维布预浸料,选用厚度为 0.2mm,直径为 5mm圆铜片作为电极材料;设备主要有美国 Agilent公司生产的34907A型多通道数据采集仪,上海精密仪器制造厂生产的 YX-25型 0.25MN半自动热压机,小型钻床,超声 F扫描仪及圆柱形落锤式冲击试验装置(冲击锤质量为 5kg,冲击头为半球状,直径为 12.5mm）。

1.2 复合材料层合板制备过程

将 G803/5224预浸料按 350mm×350mm裁剪,按照经向进行铺层(8层）,并在 1,2层间和 7,8层间按矩阵等距离(间距为 50mm×60mm）布设一定数量铜片电极(电极一半位置露在试样表面）,然后放入热压机,固化压力(0.6±0.1）MPa、固化温度180℃、固化时间 120～150min,制备复合材料层合板,板材厚度约为 2.0mm,碳纤维含量约为 70%。

1.3 性能测试与表征

模拟复合材料实际使用过程中,将复合材料层合板试样放在铁环(内、外径分别为 100mm,120mm,高为 10mm）上呈四周简支状态,冲击锤自不同高度对准铁环中心位置自由落体冲击试样不同区域,冲击区域以冲击点周围的 4个电极点标注。利用超声扫描仪对层合板受冲击区域进行扫描检测。用小型钻床对复合材料层合板上钻若干个φ5mm的孔。以层合板下表面某电极点为固定电极(钻孔实验为 B3,冲击实验为 B12）,采用多通道数据采集仪分别测量冲击或钻孔前后层合板上表面不同电极间的体积电阻值。复合材料层合板试样冲击实验装置示意图及钻孔试样如图 1所示。

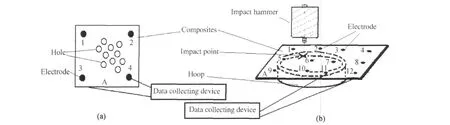
图1 复合材料实验示意图 (a）钻孔实验;(b）冲击实验Fig.1 Schematic of com posites experiment (a）drilling experiment;(b）impact experiment

2 实验结果与讨论

2.1 钻孔对碳/环氧复合材料电阻的影响

图2为钻孔后复合材料电阻变化图。从图 2中可看出,钻孔能会使复合材料的电阻变大,钻孔面积越大,复合材料电阻变化也越大。钻孔面积太小,则对复合材料电阻影响很小。只有当钻孔面积超过某一临界值(5%）,才会对复合材料电阻产生明显影响。钻孔面积为 2%时,电极点 A2电阻增大幅度最大,但只有 0.5%。钻孔面积为 6%时,电极点 A2电阻增大8.0%。另外,在孔周围的电极点变化各不相同。针对同一钻孔面积,如 15%,电极点 A2增大幅度最大,可达 27%,电极点A3增大幅度最小,仅为 0.8%。

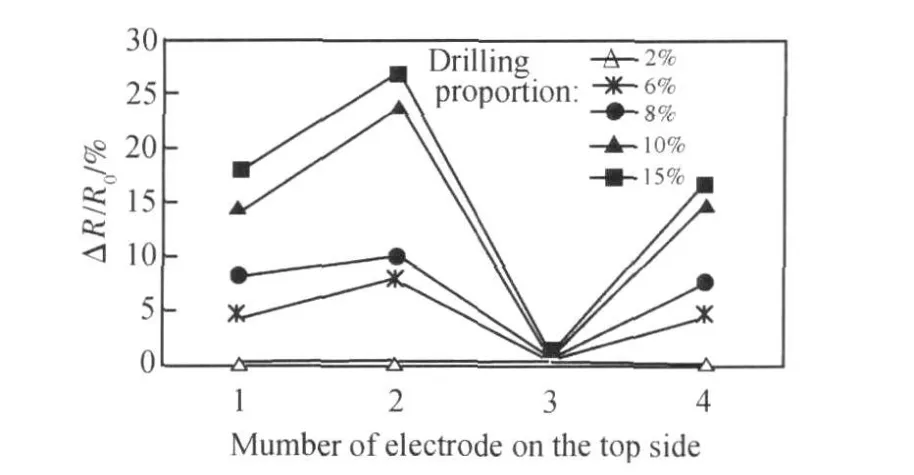
图2 钻孔后复合材料电阻变化图Fig.2 Fractional change in resistance of composites after drilling

公式(1）中,ρ为材料电导率,L为电极间距离,S为电流截面积。

复合材料的电阻 R可通过公式(1）计算:

钻孔除去复合材料板中的一部分复合材料,这样使得复合材料板在电场作用下的电流截面积减小,从而使其电阻增加。

另一方面,钻孔还使得电荷传导路线(即电极间距离 L）变长,也会使复合材料电阻增加。图 3为钻孔前后复合材料中电流示意图。从图 3中可以看出,在外加电场作用下,钻孔前(图 3a）,电荷在复合材料中是按照最近的路线(即直线）进行传导的。钻孔后(图 3b）,由于复合材料中有孔存在,则电荷必须绕过孔沿着曲线进行传导,增加了电荷传导路线。很显然,钻孔面积越大,电荷传导路线越长,复合材料电阻就将越大。而且,对于电流要绕过孔的电极点,其电阻增加更明显。

钻孔后的复合材料电阻增加幅度可以根据公式(2）进行计算:

公式(2）中,R0为钻孔前复合材料电阻,Rx为钻孔后复合材料电阻。

将 ρ,L,S代入公式(1）、(2）并整理后,可得公式(3）:

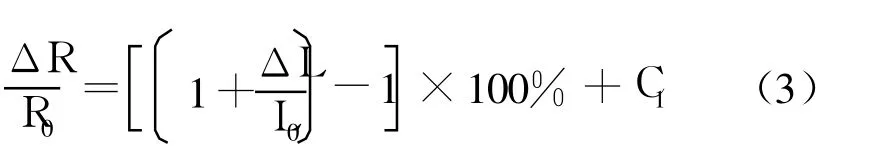
公式(3）中,L0,S0分别为钻孔前 L,S,ΔL,ΔS为分别钻孔后的变化的 L、S,C1为钻孔使复合材料电阻变化的常数项,与钻孔位置、孔径、钻孔面积有关。

为了验证公式(3）并简化计算,以钻孔影响最大的电极点 A2为例,在复合材料板中央钻 1个孔且孔径为复合材料板长度的 36%、钻孔面积为 10%(如图 3所示）时,C1为 0.031,通过公式(3）计算的复合材料电阻增大率为 23.8%,与图 2中实验数据(24%）基本一致。因此,钻孔后复合材料电阻增大 的计算模型(公式(3））是可靠的。

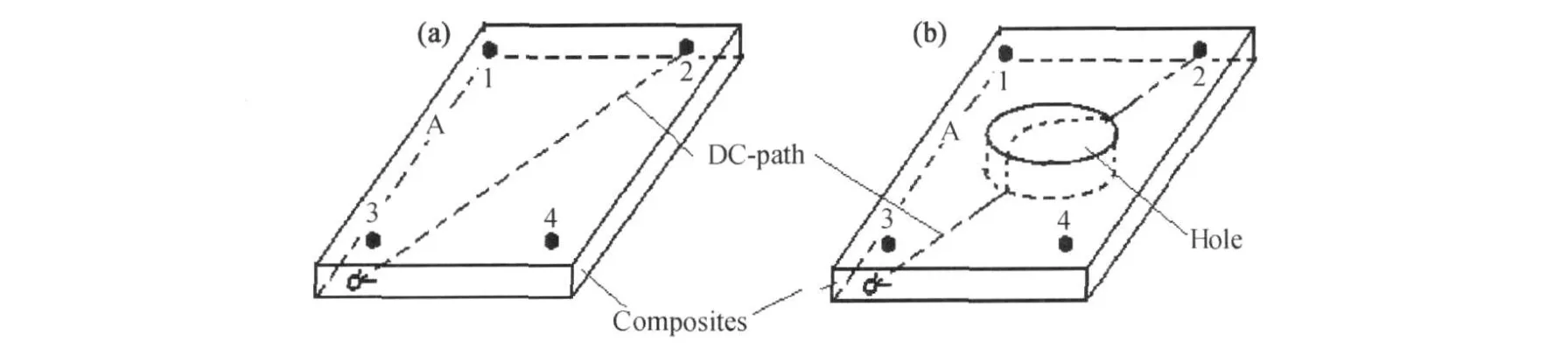
图3 钻孔前后复合材料中电流示意图 (a）钻孔前;(b）钻孔后Fig.3 Schematic of charge conducting route of composites (a）before drilling;(b）after drilling

2.2 冲击对碳/环氧复合材料电阻的影响

碳/环氧复合材料具有一定的强度,能够抵抗一定冲击能量。实验中,小于 2.0J能量冲击的复合材料层合板,目测及超声 F扫描,均未发现损伤。2.0J能量冲击的复合材料层合板,目测未发现损伤,但超声 F扫描能检测到复合材料内部有轻微的损伤(如图 4所示）。虽然,复合材料层合板上下表面看不出损伤,但从图 4中可以看出,复合材料层合板由在厚度为 1.05mm至 1.17mm之间出现了损伤,只是损伤较小,只占复合材料层厚的 6%。

图4 经 2.0J冲击复合材料超声F扫描图 (a）含最浅损伤(1.05mm）;(b）含最深损伤(1.17mm）Fig.4 Ultrasonic F-scan graph of composites after 2.0Jimpact (a）graph with the flat damage(1.05mm）;(b）graph with the deepest damage.(1.17mm）

大于 2.0J能量冲击的复合材料层合板,目测及超声 F扫描,均能发现损伤。因此,2.0J是复合材料冲击损伤能量阈值。由于复合材料较脆,所以,冲击能量超过损伤能量阈值时,能量越大,产生的损伤也越大。

由图 5可以看出,不同能量的冲击对复合材料层合板电阻影响各不相同。小于冲击损伤能量阈值的冲击,如 1.5J,会使复合材料各电极点间电阻值变小。并且,离冲击点越近的电极点电阻下降越大,最大下降 2.63%(A1）。冲击损伤能量阈值的冲击(2.0J）使冲击点周围的电极点电阻上升,但上升幅度不大,最大幅度为 2.44%(A1）。同时,远离冲击点的电极点电阻下降,下降最大幅度为 0.2%(A 12）。大于冲击损伤能量阈值的冲击,如 5.0J,在复合材料中产生穿孔损伤,冲击点周围的电极点电阻较大幅度上升,上升最大幅度为 5.34%(A1）。同时,远离冲击点的电极点电阻较大幅度下降,下降最大幅度为 3.28%(A4）。

碳/环氧复合材料是由碳布/环氧树脂预浸料为原材料,按照一定角度铺层并通过热压、固化,复合而成的复合材料,碳布之间相互接触,特别是经、纬纱交叉点接触更紧密。在外加电场下,复合材料通过碳纤维的接触点而导电。接触点之间的复合材料可以看成独立的导体,并且具有一定的电阻,若干个小导体通过串联或并联在一起。图 6为复合材料电阻示意图,RAB为 1.75R。

冲击作用会引起碳纤维之间接触状态发生变化,从而使复合材料中小导体的串、并联关系发生变化。小于冲击损伤阈值的能量冲击,如 1.5J,不但没有造成复合材料层合板分层损伤,反而使碳纤维层接触更紧密,接触面积即电流截面积 S增大。这样,复合材料中存在的不相连的小导体,经冲击后相互连接在一起,从而,引起复合材料电阻下降(如图7a中 ,RAB为 1.25R）。

图6 复合材料电路示意图Fig.6 Schematic of conductive mechanism of composites

等于或大于冲击损伤阈值的能量冲击作用,如5.0J,复合材料层合板在受冲击点及周边位置会产生穿孔及分层损伤,碳纤维之间接触点减少,接触面积即电流截面积 S减小,电荷传导路线 L也会变长,复合材料中的小导体串、并联发生断路,从而引起材料电阻上升(如图 7b中,RAB为 2.5 R）。在远离冲击点区域,受到的冲击能量小于冲击损伤能量阈值,因此,冲击作用并没有产生损伤,反而使复合材料中碳纤维的接触点增多,电流截面积 S增加,复合材料电阻 R变小。

图7 冲击后复合材料电路变化示意图 (a）低能量冲击;(b）高能量冲击;×表示电路断路Fig.7 Schematic of electric circuit in composites after impact (a）low energy impact;(b）high energy impact.×denotes disconnect of electric circuit

2.3 钻孔与冲击对碳/环氧复合材料电阻影响的比较

钻孔使复合材料产生穿孔性损伤,而且,钻孔面积即是复合材料损伤面积,公式(1）中 L,S能够具体测量出来,并根据不同的 C1,代入公式(3）可以计算出复合材料电阻变化情况。

对于冲击作用来说,只有高能量冲击,才能使复合材料产生穿孔性损伤。但是,复合材料损伤面积远大于孔的面积。孔周边的复合材料虽然损伤了,但仍然附着在复合材料板上,还能够导电。对于相等的损伤面积,与钻孔相比,高能量冲击能够使复合材料电阻增加幅度更小些。因此,对公式(3）进行一定修正得出公式(4）,从而可以根据公式(4）计算高能量冲击对复合材料电阻的变化。也就是说,能够参照钻孔的方法,比较简便地计算高能量冲击对复合材料电阻的变化。

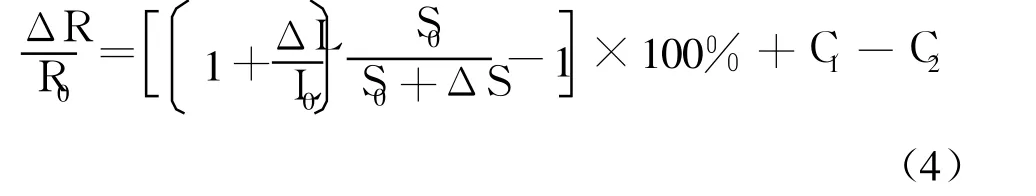
公式(4）中,C2为冲击损伤常数项,与冲击能量及冲击头形状、直径有关。本文中,C2约为 0.027。

为了验证公式(4）并简化计算,分别以损伤对其影响最明显的电极点为例(钻孔实验为 A2,冲击实验为A 1）,根据图 2中 6%钻孔面积(与 5.0J冲击产生的损伤面积相等）的相关数据,通过公式(4）可计算出 5.0J冲击作用使复合材料(A1）电阻增加 5.3%(钻孔使复合材料(A2）电阻增加 8%）,这与实验测量值基本一致。

3 结论

(1）钻孔使碳/环氧复合材料中碳纤维之间接触点减少,电流截面积减小,电荷传导路线变长,从而使复合材料电阻变化。根据钻孔模型可计算出复合材料电阻变化率。

(2）冲击作用使碳/环氧复合材料中独立导体之间的串、并联关系发生改变,从而引进复合材料电阻变化。根据修正后的钻孔模型也可计算出冲击穿孔复合材料电阻变化率。

[1]SHOUKAIWANG,CHUNG D D L,CHUNG JAYCEE H.Self-sensing of damage in carbon fiber polymer-matrix composite by measurement of the electrical resistance or potential away from the damaged region[J].Journal of Materials Science,2005,40(23）:6463-6472.

[2]于杰,王继辉,王钧.碳纤维/树脂基复合材料导电性能研究[J].武汉理工大学学报.2005,27(5）:24-26.

[3]ANGELIDISN,IRVING P E.Detection of impact damage in cfrp laminates bymeans ofelectrical potential techniques[J].Composites Science and Technology,2007,67(3）:594-604.

[4]LOUIS M,JOSHI S P.An experimental investigation of through-thickness electrical resistance of CFRP lam inates[J].Composites Science and Technology,2001,41(6）:56-65.

[5]骆心怡,王开坤,熊克,等.碳纤维复合材料单向层合板自传感特性[J].北京科技大学学报,2002,24(6）:638-642.

[6]WANG Xiao-jun,WANG Shou-kai,CHUNG DD L.Sensing damage in carbon fiber and its polymer-matrix and carbonmatrix composites by electrical resistancemeasurement[J].Journalof Materials Science,1999,34(6）:82-89.

[7]王钧,刘东,张联盟.碳纤维增强聚合物基复合材料自诊断性能研究[J].武汉理工大学学报,2002,24(4）:36-38.

[8]沈烈,益小苏.一个单向碳纤维增强树脂基复合材料导电结构模型[J].复合材料学报,1998,15(3）:66-70.

[9]XIA ZH,CURTINW A.Modeling ofmechanical damage detection in CFRPs via electrical resistance[J].Composites Science and Technology,2007,67(10）:1518-1529.

Modeling of Electrical Resistance Influence in Carbon/Epoxy Composites Result from Drilling and Impact

XIE Xiao-lin1,2,QUAN Hong-ying2,LIZhi-peng2,WANG Gao-chao2,Zhang Jian-chao2
(1.College of Materials Science and Engineering,Wuhan University of Technology,Wuhan 430070,China;2.Key Laboratory of Nondestructive Testing(Nanchang Hangkong University）,Ministry of Education,Nanchang 330063,China）

Electrical resistance of carbon/epoxy composites weremeasured before and after they were drilled or impacted separately,themechanism of electrical resistance change in composites were analyzed,the calcu latingmodelof resistance influence in composites were established.The results show thatelectrical resistance of compositeswas changed after they had been drilled or impacted,it can be ascribed to the change of contact point among carbon fibers(sectional region of electrical current）and charge conducting route in composites.Impact calculatingmodel derivate from drillingmodel can greatly simp lify the calcu lating of influence from impact on electrical resistance in composites.According to themodeling of electrical resistance influence in carbon/epoxy composites resulting from drilling and impact,the fractional change in resistance of composites can be calculated,and they coincided with the experimental results.

carbon/epoxy composites;drilling;impact;electrical resistance change;modeling

10.3969/j.issn.1005-5053.2010.1.016

TB332

A

1005-5053(2010）01-0085-05

2009-07-15;

2009-09-28

教育部无损检测技术重点实验室开放基金(ZD 200829001）

谢小林(1974—）,男,讲师,博士生,主要从事聚合物基复合材料研究,(E-mail）XXL0810@qq.com。