路面破碎机电液系统的自适应反推滑模控制
张平均 蒋新华
1.中南大学,长沙,410083 2.福建工程学院,福州,350108
0 引言
共振式混凝土路面破碎机[1]是一种新型的路面整改用工程机械,其行走机构采用液压比例泵控马达系统。电液比例系统[1-2]动态特性具有较强的非线性,且存在不确定性的模型参数和负载扰动,如压力损失、阀的非线性特性等。同时行走机构本身和作业路面的参数也存在着较大的变化,如轮缘半径的变化、路面坡度、材质和发动机速度的变化等。液压行走系统的结构和参数特征,对行走速度控制的稳态精度、动态特性造成较大的影响。
Lyapunov函数在非线性系统的自适应控制设计中具有重要的作用,但如何构造Lyapunov函数需要理论的支持,而自适应反推法[3-5]提供了一种较为简便的结构化、系统化方法,当干扰或不确定性不满足匹配条件时,具有明显的优越性。滑模控制方法[6-9]对系统数学模型精确度要求不高,算法简单,对系统参数摄动和外部扰动具有较好的鲁棒性等优点。自适应反推法和滑模控制方法之间的结合在非线性不确定控制系统中得到了应用研究[10-13]。
本文针对共振式混凝土路面破碎机行走机构液压系统的参数不确定性,采用基于自适应反推滑模的控制策略,从而保证系统控制的稳定性和高精度的速度跟踪特性。
1 路面破碎机行走机构的模型
路面破碎机行走机构是由一个行走泵驱动两个行走马达,再分别经减速机构驱动两个后轮而工作的。通过速度踏板实现行走泵排量的电比例控制,两行走马达排量根据负荷调整,分别由各自的电磁阀进行开关量控制,使马达排量达到最大或最小,从而实现对设备的行走速度进行控制。
行走机构的比例变量泵控马达系统由多个液压元件组成,可以分解为比例阀控制、泵变量机构、泵控马达速度控制组合和机械传动行走控制组合等部分,见图1。其中泵控马达组合的动态方程是建立在变量泵和马达流量平衡以及马达和负载转矩平衡方程的基础上的,在忽略马达和负载之间连接刚度的情况下,建立系统模型如下:
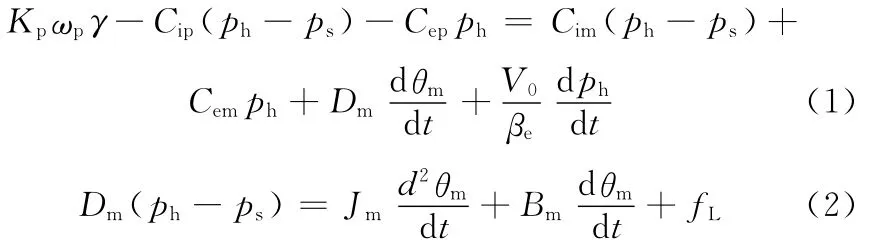
式中,Kp为变量泵的排量梯度,m3/rad;ωp为变量泵的转速,rad/s;γ为变量泵斜盘倾角,rad;Cip、Cep分别为变量泵的内外泄漏系数,m5/(N·s);Cim、Cem分别为马达的内外泄漏系数,m5/(N·s);ph、ps分别为高低压腔侧压力,Pa;Dm为马达排量,m3/rad;θm为行走马达轴转角,rad;V0为泵和马达工作腔以及连接管道的总容积,m3;βe为液压回路综合弹性模量,N/m3;Jm为折算到行走马达轴上的总转动惯量,kg·m2;Bm为折算到马达轴上的总黏性阻尼系数,N/(m/s);fL为作用行走马达轴上的总不确定性项,它包括了外负载转矩及负载扰动等的不确定性扰动。
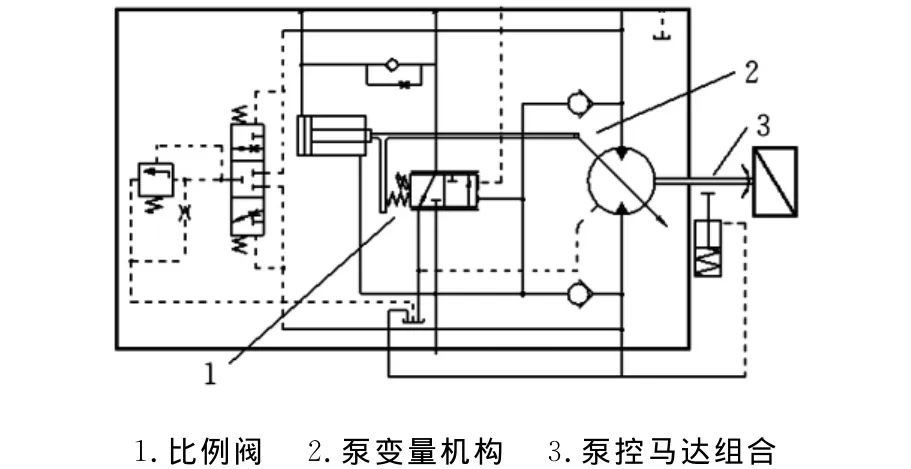
图1 破碎机行走系统液压原理图
比例泵控制组合包括了电比例方向控制阀和阀控液压缸的泵斜盘倾角调节结构,在忽略阀的频率特性情况下,等效为

式中,u为比例阀的控制输入信号;xv为比例阀阀芯位移,m;Ka为比例放大器增益;Kbv为比例阀的增益系数;Kγ为变量泵斜盘倾角系数;Kq为比例阀在稳态工作点附近的流量增益,m3/s;L为变量活塞油缸施力点与斜盘铰接点间的距离,m。
行走机械传动控制组合实现角速度到直线速度的转换和动力传递,破碎机车轮半径为0.7225m,速度检测采用75脉冲/转的旋转编码器,定义

式中,v为后轮行走速度,m/min;Kv为速度反馈回路增益;θ为后轮轴旋转角位移,rad。
基于式(1)~ 式(5),取状态变量x1=v、x2=v·,则系统的状态空间模型为

式中,ωm为液压固有频率;ξm为阻尼比;Ctp为泵泄漏系数;Ctm为马达泄漏系数;Jt为折算到测量端的总转动惯量,kg·m2。
本文的研究着重于泵控马达速度控制系统参数中的不确定性,由于系统温度、工作油压等的不同,Ct、βe及Bm等均是变化的,同时ωm、ξm明显为非线性的,因此模型中定义α1、α2、α3为作用在各环节上的不确定性参数项。在实际系统中,可以认为这些不确定性项是有界的。
2 自适应反推滑模控制器设计
2.1 自适应反推滑模控制律的设计
自适应反推设计方法是将复杂的非线性系统分解成不超过系统阶数的子系统,然后为每个子系统分别设计Lyapunov函数和中间虚拟控制量,一直后推到系统的实际控制信号,从而完成整个控制器的设计,其最大优点是最终得到的控制肯定可以保证整个系统的稳定。
系统的控制目标是马达旋转速度跟踪,定义各步的跟踪误差为e1=v-vr,其中,vr为第一步的期望值。为了使速度跟踪误差趋于零,定义第一步的Lyapunov函数为
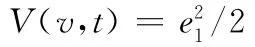
对其求导得

定义第二步的Lyapunov函数为
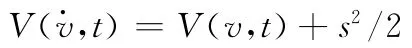
其中,s为滑模控制的切换函数,定义s=c1e1+e2,其中常数c1>0,且

对V2求导,代入s·和e·2·,有

对于系统中的不确定性参数,可以采用取其上界或平均值的方法设计反推滑模控制器为

其中,u为加在比例泵控制组合上的实际控制信号;a、b均为控制器仿真参数,a>0、b>0;α1、α2、α3、fL均为相应的平均值,可由其上下界确定。实际应用中的滑模控制系统参数的不确定性和非线性等因素影响,使得滑动模态产生高频抖振,高频抖振可能激发系统未建模部分的强烈振荡,出现超调过大、过渡过程延长,甚至出现不稳定状态,且静态指标也会降低,抖振问题己成为滑模变结构控制在工程应用中的突出障碍。如何消除抖振而又不失强鲁棒性,仍是滑模变结构控制必须解决的首要问题,下面采用自适应算法对前面定义的不确定参数项进行实时估计,以提高参数的适用性能。
2.2 稳定性分析
定义Lyapunov函数为
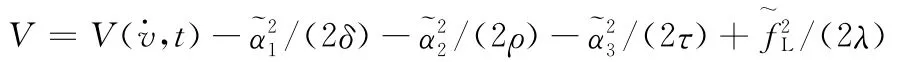
估计误差分别定义为

对其求导:
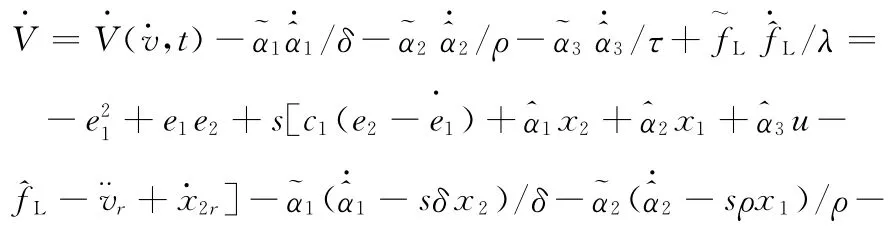
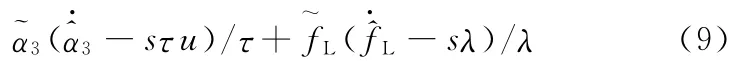
式(8)可以重写为

设计自适应律为

将式(10)、式(11)代入式(9)得

定义

3 仿真和实验结果
根据前面推导出的系统模型和控制策略,结合路面破碎机液压回路的设备选型,确定其参数的标称值如下:V0=5.0×10-4m3、Ct=2×10-10m5/(N·s)、Dm= 5.5×10-6m3/rad、βe= 2×107N/m3,Jt=0.05kg·m2,Bm=6.8×10-5N/(m/s),ph=30MPa,ωm=0.45,ξm=232,Ke=3.24,Kf=3.11,α1=22,α2=40,α3=3,fL=57。
在MATLAB6.5软件环境下对该控制系统进行了仿真实验[14],为了模拟参数的不确定性,选取fL=57sin6t,采样周期为0.001s。控制器仿真参数a=12,b=20,c1=1.1,δ=3,ρ=15,τ=18,λ=15。仿真结果如图2和图3所示。
根据图2的控制器输出us比较分析,采用自适应反推滑模控制方法时,经过一段时间调节后,控制量的颤振幅度较小,说明控制策略能根据不确定性参数项的估计值自动调节滑模校正项的控制增益,有效地抑制了控制量的颤振强度。这主要在于系统的自适应律可有效抑制参数的不确定性。

图2 两种情况下us的变化曲线

图3 速度方波响应曲线
图3 为幅值等于15m/min的方波控制下的系统速度响应,显示出具有较好的性能指标,速度动态升、降曲线符合液压系统要求,且超调较小,可以提高液压元件的安全性,稳态精度较高,可以在此基础上提高整车的节能性能。
根据图4分析,在速度的上下调节时,速度的波动曲线可以满足系统的运行要求。
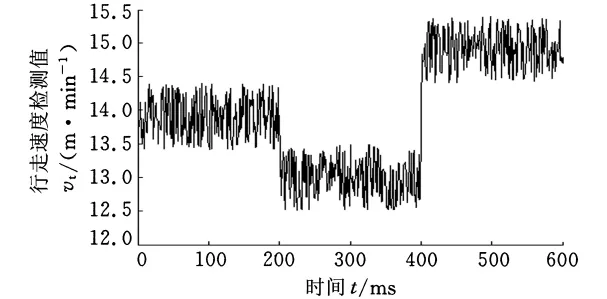
图4 行走速度调节曲线
4 结语
本文针对路面破碎机行走机构的速度控制问题,采用了自适应反推滑模控制方法,对于参数扰动及负载波动,具有较好的动态响应性能,且控制算法简单,便于工程机械车载控制系统的应用。
[1] Eugeniusz B,Miroslaw C,Witold G.Load-independent Control of a Hydraulic Excavator[J].Automation in Construction,2003,12(3):245-248.
[2] Pommier V,Sabatier J,Lanusse P,et al.Crone Control of a Nonlinear Hydraulic Actuator[J].Control Engineering Practice,2002,10(4):391-402.
[3] Guang L,Amir K.Robust Control of a Hydraulically Driven Flexible Arm Using Backstepping Technique[J].Journal of Sound and Vibration,2004,208(3/5):759-775.
[4] Kim K,Kim Y.Robust Backstepping Control for Slew Maneuver Using Nonlinear Tracking Function[J].IEEE Trans.on Automatic Control,2003,11(6):822-829.
[5] 董文瀚,孙秀霞,林岩.反推自适应控制的发展及应用[J].控制与决策,2006,21(10):1081-1087.
[6] Edwards C.A Practical Method for the Design of Sliding Mode Controllers Using Linear Matrix Inequalities[J].Automatica,2004,40(10):1761-1769.
[7] Barrolini G,Pisano A,Punta E,et al.A Survey of Applications of Second-order Sliding Mode Control to Mechanical Systems[J].International Journal of Control,2003,76(9):875-892.
[8] 徐东光,吴博,吴盛霖,等.基于模糊调节的Stewart平台积分滑模变结构控制器的设计[J].中国机械工程,2008,19(4):402-405.
[9] 段锁林,安高成,薛军娥,等.电液伺服力控系统的自适应滑模控制[J].机械工程学报,2002,38(5):109-113.
[10] 安树.反演滑模控制在BLDCM伺服系统中的应用[J].机械工程与自动化,2008,151(6):161-163.
[11] 郑剑飞,冯勇,郑雪梅.不确定非线性系统的自适应反演终端滑模控制[J].控制理论与应用,2009,26(4):410-414.
[12] Ali J,Alan S,Zinober I,et al.Adaptive Sliding Mode Backstepping Control of Nonlinear Systems with Unmatched Uncertainty[J].Asian Journal of Control,2004,6(4):447-453.
[13] 李俊,徐德民.电机驱动机械手的自适应反演变结构控制[J].机械科学与技术,2001,20(4):528-530.
[14] 刘金琨.滑模变结构控制 MATLAB仿真[M].北京:清华大学出版社,2005.

