斜角切削的热力建模与仿真分析
李炳林 王学林 胡于进 李成刚
华中科技大学,武汉,430074
0 引言
目前,切削机理的研究主要集中在相对简单的直角切削,但实际加工过程中的切削绝大多数都属于斜角切削。直角切削是斜角切削的特殊情况,它又是铣削分析的基础,所以研究斜角切削更具普遍意义。斜角切削的建模有单一剪切面斜角切削建模和平行面剪切区斜角切削建模两种。Merchant[1]参照直角切削模型,建立了单一剪切面的斜角切削模型,得出了剪切流角和切屑流角的关系。Shaw等[2]提出了以切削速度和切屑速度确定的平面为等效平面的概念。Morcos[3]用等效平面方法,通过塑性力学原理得出了斜角切削的滑移线解。Usui等[4]提出了与实际近似一致的能量解法,通过求解剪切功和摩擦功之和的最小值,得出切屑流角和法向剪切角。Shamoto等[5]把 Merchant的最小能量原理和 Lee-Shaffer的最大剪切应力原理扩展到斜角切削中,提出了计算斜角切削几何角度的数值迭代方法。
单一剪切面模型会产生速度的不连续而导致剪应变率无限大,Oxley[6]提出了直角切削的平行面剪切区模型。该模型不单纯用力学方法,而是考虑了材料的流动应力变化。剪切区的流动应力计算是预测切削力的关键。流动应力一般可由三种方法得到:第一种方法是通过切削实验测出切削力,然后逆向分析得到流动应力。第二种方法是用有限元方法。第三种方法是通过材料实验(高速高温拉伸试验或切削实验)得到材料的本构关系,然后通过建立剪切区的热力控制方程预测出流动应力。实际上,第一种方法是通过切削实验直接逆向分析得到流动应力;而后两种方法是先通过材料试验得到材料模型,然后用分析方法或数值方法间接正向预测出流动应力,这更具普遍性和实用性。在Oxley加工预测理论中有很多的未知系数,更加重要的是材料模型没有可供用的准确试验数据,在研究中很难推广。Lin等[7]把Oxley的直角切削理论延伸到斜角切削上。Moufki等[8-9]假设垂直于剪切面方向的静水压力分布是常数,并考虑运动方程中的惯性项,建立了斜角切削流动应力的计算方法。但对一般的切削加工,塑性流动产生的惯性力可以忽略[10]。
本文提出一种建立斜角切削热力模型的新方法,其核心是围绕剪切区流动应力的计算。通过定义等效平面角来确定等效平面的方位,用坐标变换法分析了斜角切削中的向量关系。在剪切区,采用不等分剪切区模型,建立了应变、温度和应力的控制方程,并考虑了材料的加工硬化和热软化对流动应力的影响,最后通过流动应力计算出切削力。所提出的斜角切削分析预测方法不需要额外的实验测试,仅需材料属性和切削条件就能预测出切削力。
1 斜角切削的几何关系
图1定义了斜角切削相关的切削参数,其中λs为刃倾角,γn为法前角,a为切削厚度,b为切削宽度。先定义7个坐标系,这些坐标系定义在基平面Pr、切削平面Ps、法平面Pn、剪切平面Psh、前刀面Aγ、等效平面Pe上,如图2所示。

图1 斜角切削示意图

图2 斜角切削的几何关系
(1)坐标系(xo,yo,zo)。xo平行于切削速度,yo和zo确定Pr,xo和yo确定Ps。
(2)坐标系(xn,yn,zn)。yn平行于切削刃,xn和zn确定Pn,zn平行于zo。
(3)坐标系(xr,yr,zr)。yr平行于yn,yr和zr确定Aγ,zr垂直于切削刃。
(4)坐标系(x,y,z)。y平行于yn,x和z确定Pn,z垂直于Psh。
(5)坐标系(xc,yc,zc)。zc为切屑流方向,yc和zc确定Aγ,xc平行于xr。
(6)坐标系(xs,ys,zs)。xs为剪切流方向,xs和ys确定Psh,zs平行于z。
(7)坐标系(xe,ye,ze)。xe平行于xs,xe和ze确定Pe,ye垂直于等效平面。
坐标系(xo,yo,zo)绕zo轴旋转角度λs得到坐 标 系 (xn,yn,zn)可 表 示 为:(xo,yo,zo)转变换关系如图3所示,其中,φn为法向剪切角,ηc为切屑流角,ηs为剪切流角,ηe为等效平面角。

图3 坐标系之间的旋转变换关系
2 斜角切削的运动分析
斜角切削常用的分析方法有两种:一种是法平面法[1,5],另一种是等效平面法[2-4]。等效平面是由切削速度和切屑速度决定的平面,把斜角切削机理看作是二维切削状态的累积。本文定义了等效平面角来确定等效平面的方位,有

因等效平面通过xo,所以xo在垂直于等效平面的ye方向的投影等于零,于是有

材料流在剪切带的始剪切线处的合速度等于切削速度;在剪切带的终剪切线处的合速度等于切屑速度,如图4所示。
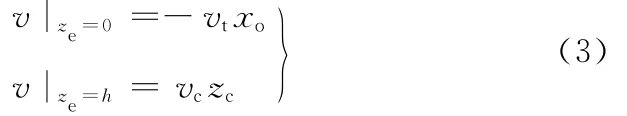
式中,v为材料塑性流动速度;vt为切削速度;vc为切屑速度。

图4 等效平面上剪切区的示意图
根据材料在塑性变形时,速度场必须满足不可压缩假设[10],可以得到切削速度vt与切屑速度vc之间的关系:

3 控制方程
3.1 材料控制方程
由于Johnson Cook(JC)模型的准确性和简洁性,很容易推广到其他材料,所以本文材料模型采用常用的JC本构方程表示:

式中,A、B、C、n、m 均为材料常数;γ为剪切应变;γ·为剪切应变率;γ·0为参考剪切应变率;T为绝对温度;Tr为参考温度;Tm为熔化温度。
3.2 变形控制方程
在等效平面Pe(xe,ze)中,由相容条件可得剪应变率γ·和速度场的关系有

式中,vxe、vze分别为材料在xe和ye方向上的速度。
γ·也是应变γ的随体导数。因为在稳态流假设条件下,γ的时间偏导数等于零,所以有

式中,t为时间。
剪切区是一个非常窄的区域(合理的平均值大约 是 0.025mm[11]),且 有 很 高 的 应 变 率。Oxley[6]的实验结果显示应变率在两个边界剪切线处近似等于零,而在中间的主剪切面上达到最大。Astakhov等[12]提出把剪切区分为宽区和窄区,并用切屑的显微照片和微硬度法验证了分为两个不等区的正确性。Tounsi等[13]采用不等分剪切区模型,并假设直角切削中剪切区的应变率呈不对称的分段线性分布,并由此识别出了材料JC模型的常数。在等效平面Pe上,本文采用了直角切削中的不等分剪切区模型,如图4所示。主剪切面Psh把剪切区分成两个不等的部分,划分系数为k(0<k<1)。在主剪切平面Psh上,剪应变率达到最大值γ·max,而剪切方向速度被认为等于零。根据Tounsi等[13]的剪应变率在剪切区呈分段线性分布假设,剪应变率可表示为
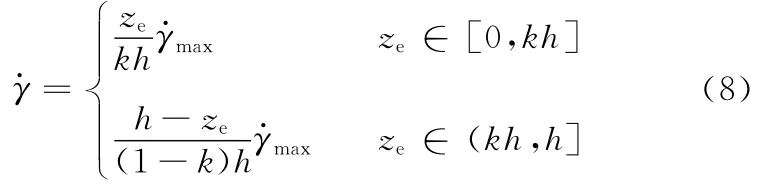
式中,h为剪切区厚度。
联立式(7)和式(8),考虑到在始剪切线处的应变等于零,对ze积分得

联立式(6)和式(8),可得

式中,vxe(0)、vxe(h)分别为材料速度在始剪切线和终剪切线处xe方向上的分量。
主剪切面被定义为剪切方向速度等于零的平面,所以有

由式(11)可得
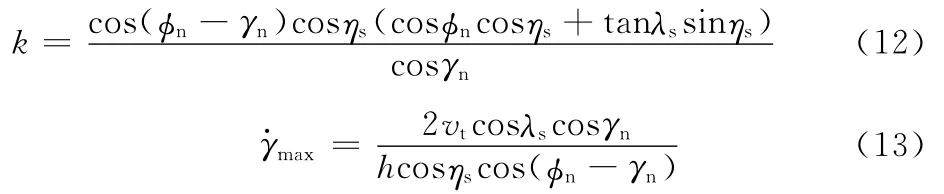
把式(12)和式(13)代入式(8)、式(9)和式(10)中,就可得到剪切区的剪应变率、剪应变和剪切速度的分布。
3.3 温度控制方程
假如塑性变形功中转化成热量的分数(Taylor-Qinney系数)为μ,在切削过程中,通常可以把剪切区看成绝热情况,因此热导率λ=0。在稳态流情况下,二维热传导方程可简化为

式中,ρ为材料密度;c为质量热容。
式(14)的一个热力边界条件为:切屑在始剪切处的温度等于初始工件温度Tw,即

初始工件温度近似等于室温。
上述式(5)、式(8)、式(9)、式(10)和式(14)是工件材料在剪切区的热力控制方程,其中γ和γ·是关于ze的函数,τ是关于ze与T的函数,所以式(15)是T关于ze的一阶常微分方程,对其进行数值积分,就可得到剪切区的温度分布,然后回代入式(5)中,即可得到剪切区的剪应力分布和主剪切面上的剪应力值。
4 切削力的计算表达式
假设主剪切平面上的剪切应力是均匀分布的,剪切力Fs与剪切应力τs成正比例,可得

设Fns为垂直于主剪切面上的正压力,由作用在切屑上的力平衡关系可得
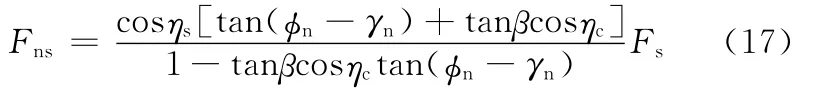
式中,β为刀具与切屑面之间的平均摩擦角。
在斜角切削中,切削力Fc、背抗力Fd、进给力Ff是切削合力F在单位向量xo、yo、zo方向上的分量,可表示为矩阵形式:

在计算切削力时,法向剪切角φn、平均摩擦角β和剪切流角ηc都是未知角。可以假设斜角切削中法平面的剪切角满足Merchant公式:
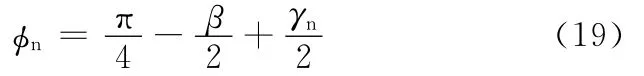
刀具与切屑面之间的平均摩擦因数f由Schulz[14]的经验公式得出

式中,f0、p为常数。
联立式(4)、式(19)和式(20),即可得到法向剪切角和平均摩擦角。剪切流角可由Moufki等[8]的隐式方程迭代计算,可以表示成下面形式:

5 仿真与分析
5.1 42CrMo4钢
为了验证提出模型的正确性,将仿真结果与Mou f ki等[9]的斜角切削实验数据作比较。42CrMo4钢的流动应力数据和热-物理属性如下:A=612MPa,B=426MPa,C=0.008,n=0.15,m =1.46,γ·0=0.0011/s,Tm=1800K,Tr=300K,ρ=7800kg/m3,λ=54W/(m·K),c=500J/(kg·K)。
其他已知参数:h =0.025mm,μ =0.85,Tw=300K,f0=0.704,p=-0.248。
本文预测结果与Moufki等[9]的实验结果均列于表1。切削力、进给力和背抗力的仿真与实验结果见图5、图6和图7。从图5、图6和图7中可以得出,实验和预测的切削力、进给力和背抗力的变化趋势是一致的,但存在一定的误差。影响误差的主要因素如下:

图5 切削力的预测与实验结果

图6 进给力的预测与实验结果
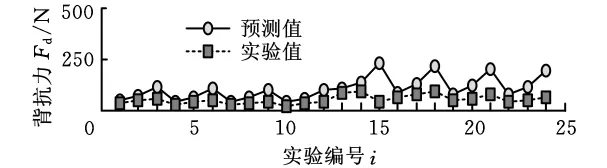
图7 背抗力的预测与实验结果
(1)切削刃半径的影响。本文公式推导中假设切削刃绝对锋锐,事实上切削刃总存在刃口半径。因为刀具刃口半径会引起产生犁耕力,导致实验力比预测力偏大。
(2)摩擦因数的影响。刀具与切屑面之间的平均摩擦因数主要依赖切屑速度、平均温度和平均正压力影响。式(20)的经验公式只考虑了切屑速度对摩擦因数的影响,而没有考虑切削厚度对摩擦因数的影响。事实上当切削厚度的增大时,会产生更多的切削热而导致刀具与切屑面的摩擦因数的下降。
(3)剪切带厚度的影响。由于准确地测量各种情况下的剪切带厚度是很困难的,本文取了典型剪切带厚度值h=0.025mm[11]。但实际上切削厚度增大,剪切带厚度也较大。
(4)材料流动应力数据的影响。Moufki等[9]的流动应力数据是通过高速变形实验得到的,实验过程中材料的应变、应变率和温度没有达到切削过程的大应变、高应变率和高温的特殊条件。

表1 42CrMo4钢的斜角切削实验[9]与本文预测结果(γ0=0°,b=3mm)
影响切削力、进给力和背抗力大小的主要因素有:
(1)切削厚度。图8给出了本文的预测值与文献[9]的实验数据,从图8可以看出预测的结果是切削力与切削厚度成正比变化,但在较大的切削厚度时与实际测量结果有较大差异,这是由于平均摩擦因数公式(式(20))中没有考虑切削厚度对摩擦因数的影响。在考虑切削厚度对摩擦因数的影响情况下,切削厚度增大,产生更多的热,摩擦因数减小,切削力又要减小。综合正反两个方面的作用,切削力不与切削厚度成正比例增大。
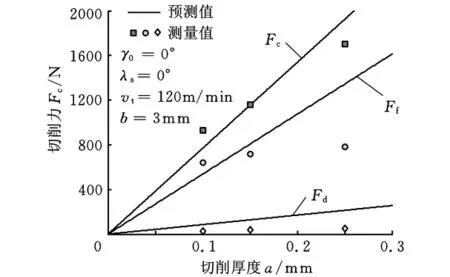
图8 切削厚度对切削力的影响图
(2)切削速度。在中速情况下,切削力一般随切削速度的增大而减小,如图9所示。

图9 切削速度对切削力的影响
(3)刃倾角。从图10可以发现,切削力和进给力不依赖于刃倾角的变化,但是对背抗力的影响较大,背抗力随刃倾角的增大而增大,这与Lin等[7]的预测结果是一致的。
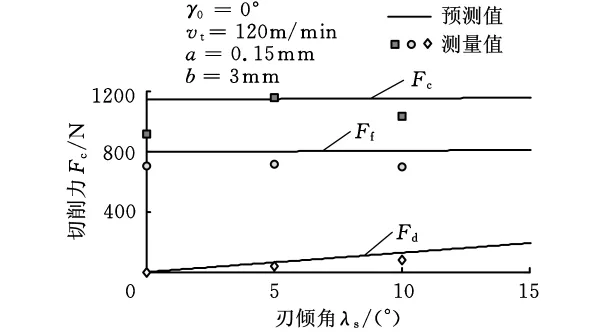
图10 刃倾角对切削力的影响
5.2 45钢
为了进一步说明提出的斜角切削模型对立铣加工同样适合。本文对45钢做了切削实验,如图11所示。45钢的JC常数[15]:A=507MPa,B=320MPa,C=0.064,n=0.28,m=1.06。刀具参数:HSS立铣刀,半径为16mm,名义螺旋角为30°,径向法前角为15°,刀齿数为3。切削参数:切削深度为5mm,切削层公称宽度为4mm,主轴转速为600r/min,每齿进给量为0.06mm。走刀路线:直线。铣削方式:逆铣。通过把立铣刀的切削刃离散成一系列的微元斜角切削单元,计算出立铣的切削力,具体的计算方法参考文献[16]。

图11 立铣加工实验
仿真和实验结果如图12所示。从图12可以发现,仿真结果和实验测量在X方向和Y方向较一致,在Z方向上有较大的误差,但这对加工精度的影响很小。需要说明的是,本文提出的模型具有普遍性,不仅可以用于铣削的建模,也可用于其他切削加工方法的建模,如车削和钻削。

图12 立铣切削力的验证
6 结束语
本文提出了一个新的斜角切削热力模型。定义了等效平面角来确定等效平面的方位,把不等分剪切区的直角切削理论延伸并应用到斜角切削中。在求解切削力时,通过建立剪切区的剪切速度、剪应变、剪应力和切削温度的控制方程,考虑了加工硬化和热软化对流动应力的影响。提出的斜角切削模型为复杂的铣削和钻削建模分析奠定了理论基础。将仿真结果和已有文献的斜角切削数据进行了对比,验证了提出模型的有效性,立铣削加工实验说明了提出的斜角切削模型普遍适用于其他具有复杂切削刃的加工建模。
[1] Merchant M E.Basic Mechanics of the Metal Cutting Process[J].Journal of Applied Mechanics,1944,A66:168-175.
[2] Shaw M C,Cook N H,Simth P A.The Mechanics of Three-dimensional Cutting Operations[J].Transactions of the ASME,1952,74:1055-1064.
[3] Morcos W A.A Slip Line Field Solution of the Free Continuous Cutting Problem in Conditions of Light Friction at Chip-tool Interface[J].Journal of Engineering for Industry,1980,102:310-314.
[4] Usui E,Hirota A,Masuko M.Analytical Predictions of Three Dimensional Cutting Process Part 1:Basic Cutting Model and Energy Approach[J].Journal of Engineering for Industry,1978,100:222-228.
[5] Shamoto E,Altintas Y.Prediction of Shear Angle in Cutting with Maximum Shear Stress and Minimum Energy Principles[J].Journal of Manufacturing Science and Technology,1999,121:399-407.
[6] Oxley P L B.Mechanics of Machining[M].Chichester:Ellis Horwood,1989.
[7] Lin G C I,Mathew P,Oxley P L B,et al.Predicting Cutting Forces for Oblique Machining Conditions[J].Proceedings of the Institution of Mechanical Engineers,1982,196:141-148.
[8] Moufki A,Dudzinski D,Molinari A,et al.Thermoviscoplastic Modelling of Oblique Cutting Forces and Chip Flow Prediction[J].International Journal of Mechanical Sciences,2000,42:1205-1232.
[9] Moufki A,Devillez A,Dudzinski D,et al.Thermomechanical Modelling of Oblique Cutting and Experimental Validation[J].International Journal of Machine Tools and Manufacturing,2004,44(9):971-989.
[10] Johnson W,Mellor P B.Engineering Plasticity[M].New York:John Wiley &Sons,1983.
[11] Shaw M C.Metal Cutting Principles[M].Oxford:Oxford University Press,1984.
[12] Astakhov V P,Osman M O M,Hayajneh M T.Re-evaluation of the Basic Mechanics of Orthogonal Metal Cutting:Velocity Diagram,Virtual Work Equation,and Upper Bound Theorem[J].International Journal of Machine Tools and Manufacturing,2001,41(3):393-418.
[13] Tounsi N,Vincenti J,Otho A,et al.From the Basic of Orthogonal Metal Cutting Toward the Identification of the Constitutive Equation[J].International Journal of Machine Tools and Manufacturing,2002,42(2):1373-1383.
[14] Schultz H.High-speed Machining[M].Carl Hanser:Munich,1996.
[15] 陈刚,陈忠富,陶俊林,等.45钢动态塑性本构参量与验证[J].爆炸与冲击,2005,25:451-456.
[16] Altintas Y.Manufacturing Automation:Metal Cutting Mechanics,Machine Tool Vibrations and CNC Design[M].London: Cambridge University Press,2000.

