车辆担保期内产品质量问题早期预警研究
涂华刚 林 燕 吴有成 金 平
上海大众汽车有限公司,上海,201805
0 引言
企业担保期内的索赔数据在可靠性工程中有许多重要的应用[1-6],其中一个重要的应用和挑战是,利用该数据与生产数据、销售数据结合,对产品在市场上可能发生的质量问题进行早期检测[7-8]。
本文在分析整车企业质量担保期内的索赔数据的特性基础上,提出了一种综合千车故障数控制图的市场质量问题早期监控策略,并就其核心算法原理、算法步骤、参数优化设计、系统实现以及实例分析等多个方面展开了较为详细的论述。研究结果对于整车企业研究并监视其产品售后市场质量状况具有借鉴意义。
1 索赔数据的统计特性分析
索赔数据的生命周期包含四个重要的时间特征,分别是生产日期tprod、销售日期tsold、修理日期trepair及结算日期或索赔数据接收并确认日期treport。一个索赔数据的生成需经历以下三个时间阶段:从车辆生产完毕到车辆销售成功的时间阶段T1(即销售时间),T1=tsold-tprod;从车辆开始使用到进维修站修理的时间阶段T2(即售后使用时间);T2=trepair-tsold;从索赔申请提出到认可或结算的时间阶段T3(即数据接收及确认的时延),T3=treport-trepair,T3为结算日期和索赔申请填报的修理日期的间隔天数。
销售数据滞后T1的分布是影响故障率统计的一个重要分布。如果等待时间T1较短,会因抽样量过小,涵盖不全而导致一部分抽样误差出现,致使估计的变异性增大。只有足够大的销售月份偏移(offset)才能减小因抽样误差而带来的影响。
现以某公司2004年的真实统计数据为例来分析索赔数据滞后T3的分布。该公司索赔申请的流转时间为30天之内的约占总数的22%,60天内的约占80%,90天以内的约占95%,120天以内的约占99%。也就是说,一个索赔申请从提出到认可的整个过程所需时间T3约有3~4个月。即使在这段时间内生产过程发生了系统性变化,也很可能无从得知。这种数据滞后状况的客观存在,严重影响着故障率统计数据的及时性和完整性,这对于提早发现市场新问题和质量波动情况是极为不利的[4-6]。
抽样等待时间间隔T的选择取决于所需监控的使用月份数、数据填充的饱和度以及估计误差的大小。其中T2即为所需监控的使用月份数(month in service,MIS),数据填充饱和度受T3影响,T1影响估计误差的大小。
从以上分析可知,在一个生产周期内生产的车辆由于销售时间T1的不同往往会具备不同的售后表现,且给定使用时间T2的索赔往往也分布在几个不同的月份,因此需要三个维度对索赔数据进行多元分析[7]。
2 千车故障数及其历史平均水平的定义和计算
整车或零部件的千车故障数是一个很重要的指标,常用于描述轿车的质量,其计算公式如下:
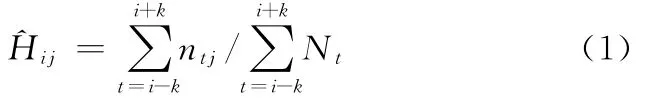
式中,ntj为生产月份t在给定使用月份j下所发生的实际故障数;Nt为给定车型在第t个生产月份下的抽样量;k为指定的第i个生产月份下的前后月份偏移,k=0,1或2。
在新车上市阶段,如t≤0,可令ntj=0,Nt=0。
千车故障数的历史平均水平的计算公式如下:
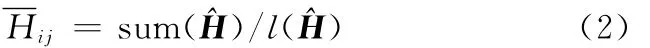
式中,Hij为第i个生产月份在第j个使用月份下对应的千车故障数历史平均水平;^H为指定历史跨期((i-m,i-1)下各生产月份千车故障数估计值的截尾向量;l(^H)为向量^H的长度。
为恰当反映出最近历史的千车故障数真实状况,同时避免因个别月份批量性千车故障数高点而对历史平均水平的影响,本文采用各历史时刻千车故障数估计值的移动截尾算术平均值作为千车故障数的历史平均水平。通过采用历史跨期中千车故障数介于25及75分位内的数据,可以将这段时期内千车故障数的历史平均变化受批量问题的影响减小到最小。根据式(2),可得两端截尾月份数lm为
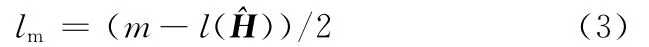
其中,m为定义的历史时间跨度,m越大,千车故障数历史平均水平表现出来的波动越平稳;但缺点是,对千车故障数的波动不能及时把握,会出现上升斜坡过长,报警的点数过多等现象。通常取m=12,即对过去一年千车故障数平均水平予以评价。当m=12时,可计算出截尾月份数lm=3。计算lm的目的是为了排除因批量问题的发生对历史平均水平的影响,以提升侦测时的灵敏度。
在新车上市阶段,历史时间跨度m可以通过以下公式获得:m=ED-ST,其中,ED为历史终点,即ED=i-(k+1);ST为历史起点,即ST=ED-12(最近一年)+1;如果ST <1,那么令ST=1。
历史时间跨度m及两端截尾月份数lm的选择可参考表1所示的规则表。
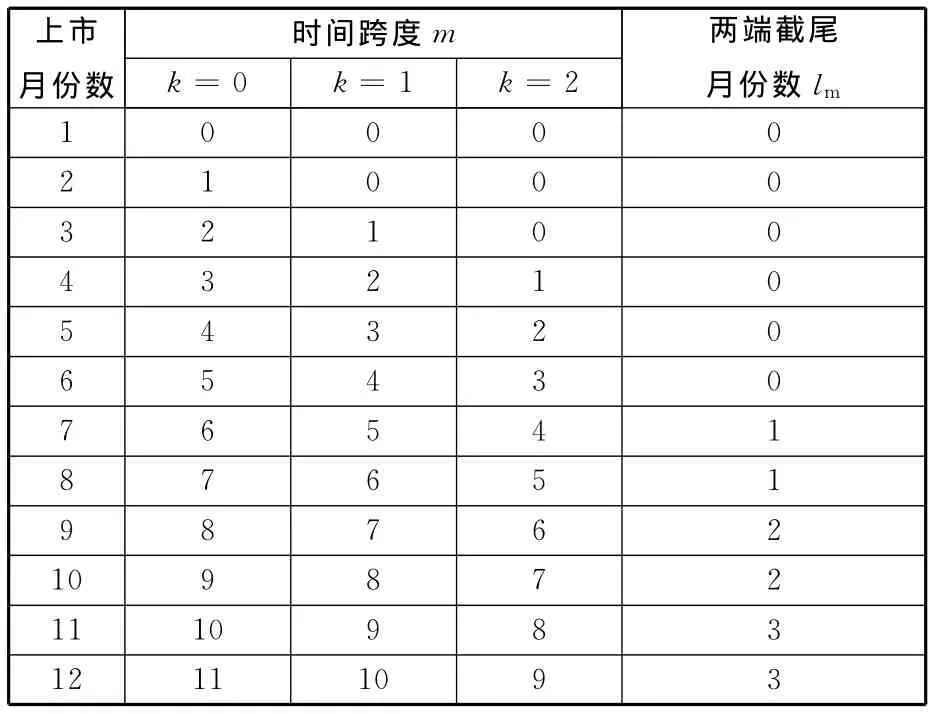
表1 历史时间跨度及两端截尾月份数选取规则表
3 千车故障数综合控制图
对于一个给定的生产周期,在一定的抽样等待时间间隔T下,不同售后使用时间的故障率变化情况,可以通过比较实际故障率和预期故障率的大小来进行监控。其假设检验可表示如下[7]:

其中,对于售后使用时间j而言,λj代表实际的故障率而λ0j代表预期的故障率。
一般来说,我们认为:如果Sij>Cij,对于第i为第i个生产周期生产的在第k个销售周期出售的、处于第j个售后使用时间段的车辆的索赔数量;Cij=,Cij为索赔总数量的临界值,Uikj为第i个生产周期生产的在第k个销售周期出售的、处于第j个售后使用时间段的车辆的预期索赔数量临界值。Uikj与千车故障数的历史平均水平Hij、生产后各个销售周期内车辆的销售数量Nik及误报警概率α有关。
然而,在实践中我们发现,当不合格数比率p即产品故障率以千车故障数为衡量基准时,基于上述原理设计的控制图会遭遇零一决策(zeroone decision)、较高误报警概率以及无法监视过程的瞬间变化等缺点[8]。
为了克服上述缺点,本文根据综合控制图(synthetic control chart)[9-17]原理构建了综合千车故障数控制图(Syn G)。Syn G控制图利用了合格连串长度(CRL)以监视基于千车故障数的不合格数比率p的变化。CRL定义为两个不合格品间的合格品长度(包含最终的不合格品)。使用CRL监视p变化的基本思想是:当p值变大,CRL值将期望变小;当p值变小,CRL值将期望变大。
由于CRL服从参数p之几何分布,其期望值E(CRL)与累积分布函数F(CRL;p)分别为

在误报警概率α下,CRL控制图之双边控制上下界限分别用UCL、LCL表示,可得
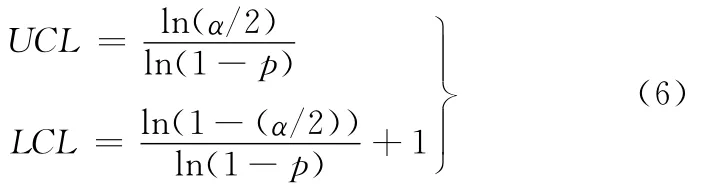
CRL控制图之平均连串长度ARL定义为CRL控制图显示控制外信号平均所需的样本点数,可由下式计算获得[8]:

在实际运用中,如果仅需监控质量变差的情况,则只需单边检验,由式(5)计算获得[10]:
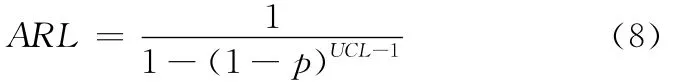
为进一步提升属性控制图的监视效率,考虑到生产过程的连续性问题,本文提出了算术加权移动平均Syn G控制图来克服生产过程中相关性问题所带来的影响。Syn G控制图的基本设计思想是,将CRL控制图中合格及不合格品视为Shewhart控制图中样本点未超出及超出其上控制边界(监视千车故障数的增加,Shewhart控制图仅需上控制边界)的样本,CRL控制图中监视的不合格数比率即为Shewhart控制图中样本点超出其上控制边界的概率。其算法步骤如下:
(1)在平均运行长度ARL指标约束下,对单边检验(one-sided test)下的控制边界(upper control bounds,UCB)及合格串长度CRL进行综合优化设计,以决定Shewhart控制图之上边界UCB*,CRL控制图之下边界L*。
(2)计算监视月份在样本大小为N下的千车故障数G 值,G =^Hij。
(3)当G落于Shewhart控制图之接受区域,此样本视为CRL控制图之合格样本,转步骤(2);反之,此样本视为CRL控制图之不合格样本,转步骤(4)。
(4)计算目前样本与上次视为不合格样本之样本长度(此次不合格样本列入计算但不包含上次不合格样本),此长度视为CRL控制图之CRL观测值。
(5)若L*≤CRL,过程视为仍处于控制内状态,转步骤(2);反之,过程被认为可能已改变至控制外状态,转步骤(6)。
(6)综合控制图显示为控制外信号,即发出预警。
(7)对各车型所有零件重复上述步骤,找出所有可能风险零件列表。
(8)对所有风险零件按模糊层次分析法进行排序,确立各车型质量整改项目。
(9)展开质量分析,找出并消除导致质量问题系统性变差的可归属原因。当过程回复至控制内状态后,转步骤(2)。
4 参数优化设计
Syn G控制图的设计通常基于ARL的表现,即当过程处于控制内状态时,ARL必需较长,以保证较低的误报率;当过程处于控制外状态时,ARL必需较短,如此才能迅速发现过程的变化。
参数优化设计过程如下:
(1)给定控制内平均显示时间(ARL1)以及CRL控制图之边界参数L(L为正整数),从L=2开始,计算千车故障数G落于Shewhart控制图之拒绝区域之外的概率α,由式(5)和式(8)可知:
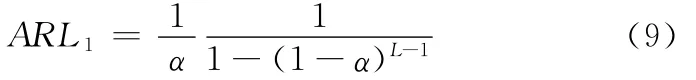
(2)当过程变坏导致千车故障数增加时,假设欲监测的控制外千车故障数为G+ΔG,其中ΔG为千车故障数增量,ΔG>0。当抽样量为N时,根据步骤(1)求得的α,通过求解以下方程组,可得控制外漏报警概率β:

其中,UB 为Shewhart控制图之控制边界,Fαν11ν12、Fβν21ν22分别为临界值为α,自由度为ν11、ν12及临界值为β,自由度为ν21、ν22的F累积分布函数,它们是β的函数。控制内误报警概率α表示生产正常情况下,纯粹是由于偶然因素导致仍有一部分点子落入Shewhart控制图之控制边界拒绝域之外的概率。控制外漏报警概率β表示当生产发生异常波动时,仍有一部分点子可能会落入Shewhart控制图之控制边界可接受域之内的概率。千车故障数增量ΔG>0,表示系统状态变差。
将求出的β值代入下式,即可求出控制外平均运行长度ARL2:
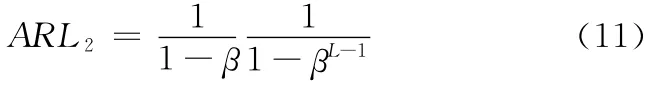
(3)如果目前之G+ΔG控制外ARL2大于前一个,转步骤(4);否则,L←L+1,转步骤(2)。
(4)将前一个(L*,α*)组合,作为综合控制图的最佳设计参数。
(5)根据最佳设计参数组合(L*,α*)、待评价生产月份在最近一年内的千车故障数的历史平均水平Hij,及待评价生产月份样本大小N,由下式可得Syn G控制图的控制边界

式中,λ(k)为记忆修正因子。
在实际设计时,针对实际千车故障数可能出现的较大过程偏移,可以采用监控长度ARL2≤3作为参数优化设计界限,来筛选固定优化参数(L*,α*)以简化Syn G控制图的设计。仿真结果显示,虽然Syn G控制图是为针对某特定欲监视过程偏移而设计的,但所有过程偏移之控制外ARL2均较Shewhart控制图低。
此外,为了进一步提升大的过程偏移的监视效率,诸如阶跃变化的过程偏移监视效率,通常还需指定一个千车故障数上边界USB,USB可通过尽可能降低误判概率α获得。令ARL1=12000,L→∞,这时可得误报警概率α=0.000 083,将其代入式(12)可得指定的故障数控制上边界USB,超过该指定控制上边界USB的监视月份将予以直接预警。
另外,为了提升问题预警的鲁棒性(robust),我们还精选了遍布全国的27家中心维修站(27SST),并以江苏、浙江、上海等核心销售区域为抽样重点进行数据监控。这些地区的索赔信息可能并不一定通过索赔结算系统的校验,但是通过利用27SST的快速反馈信号,并采用一种所谓变抽样区域(VSS)的方法,可以一定程度上确保知道目前显示的样本过程是否的确发生了系统性变化。
5 层次分析
本文采用层次分析法来筛选出真正意义上有风险的零件,并按优先级顺序排序,以便质量保障部门能够将纷繁复杂的质量信息集中加以管理,并实施集中统一协调。风险指数η的定义如下:

式中,ω为风险权重,时间越近权重越大;IO用来表示在对应的生产月份(month of production,MOP)和使用月份MIS是否有异常,为二元逻辑变量(TRUE,FALSE);mop1、mop2分别为关注的生产月份范围起止点,通常为一年或三个月;mis1、mis2分别为关注的使用月份数范围起止点。
在企业具体实践过程中,预警风险指数仅仅是层次分析所考虑的因素之一。索赔费用、是否为新增故障模式、措施落实情况、车型产销量、问题的复杂性因素、用户抱怨强度、安全性因素、概率损失,以及供应商水平等因素,都应该加以考察。
6 应用效果及预警实例
本文提出的设计思想和方法,已经在上海市重点产品质量攻关项目——上海大众汽车有限公司市场质量信息预警系统(MOP/MIS预警系统)中得到了应用和实施,取得了良好的应用效果。以某车型某零件为例,其使用3个月(3MIS)的预警曲线如图1所示,其数据状态更新日期为2007-11-06,横坐标为生产月份(“0411”表示2004年11月份,其余类似)。图1中虚线表示基于上述预警算法所构建的预警系统认为可能有问题的生产月份。从图1中可以看出,在2006-07~2006-11月中,过程控制环节出了一点小问题(壳体合模线未修导致泄漏)而影响了千车故障数曲线,接着正如我们所预料的那样,从2007-05起千车故障数曲线一直呈明显变坏的趋势。此外,该零件按上述层次分析中的风险排名规则已列在第2位。通常,这样的零件展示给主管工程师的信号应该是非常严重的。后经分析证实,该零件的模具在2007-05月时已出现严重老化问题。作为对比,按照传统的MOP/MIS系统(不带预警功能)中传统的抽样等待间隔来计算,在2007-11数据更新当月,其使用3个月的千车故障数至多只能展示到2007-04月份,即2007-04以后的点将无法展示,更不用说评价其好坏。另外,如果此时仅按其综合平均千车故障数排名来计算的话,其整车排名则排在第196位,展示给质量分析工程师的印象是,该零件的质量状况还是比较令人满意的,根本看不出什么意外。该预警系统使专业部门发现市场出现可靠性问题的时间比以前足足早了4个月。

图1 某车型某零件的预警实例
实践表明,该预警系统已成为上海大众汽车有限公司监视售后市场质量变化的重要工具。该预警系统的应用不仅全面提升了企业质量管理和监控的能力,而且可为企业每年节约1800万元以上的索赔费用,其有效性已经在企业的生产实践中得到了充分的验证。
[1] Karim M R,Suzuki K.Analysis of Warranty Claim Data:a Literature Review[J].International Journal of Quality & Reliability Management,2005,22(7):667-686.
[2] 张建国,许海宝.汽车质量保证期故障信息的可靠性分析方法[J].中国机械工程,2000,11(5):544-548.
[3] Attardi L M,Guida G.Pulcini.A Mixed-weibull Regression Model for the Analysis of Automotive Warranty Data[J].Reliability Engineering & System Safety,2005,87(2):265-273.
[4] Alam M M,Suzuk K.Reliability Analysis of Automobile Warranty Data Using Censoring Information Related to Random Failures[C]//Proceedings of the 5th Asian Quality Congress.Incheon,Korea,2007:542-547.
[5] Rai B,Singh N.Hazard Rate Estimation from Incomplete and Unclean Warranty Data[J].Reliability Engineering & System Safety,2003,81(1):79-92.
[6] Rai B,Singh N.Forecasting Warranty Performance in the Presence of the‘Maturing Data’Phenomenon[J].International Journal of Systems Science,2005,
36(7):381-394.
[7] Wu H,Meeker W Q.Early Detection of Reliability Problems Using Information from Warranty Databases[J].Technometrics,2002,44(2):120-133.
[8] Xie M,Lu X S,Goh T N,et al.A Quality Monitoring and Decision-making Scheme for Automated Production Processes[J].International Journal of Quality and Reliability Management,1999,16(2):148-157.
[9] Honari B,Donovan J.Early Detection of Reliability Changes for a Non-Poisson Life Model Using Field Failure Data[C]//RAMS 2007Proceedings.Orlando,2007:346-349.
[10] Huang H,Chen F.A Synthetic Control Chart for Monitoring Process Dispersion with Sample Standard Deviation[J].Computers and Industrial Engineering,2005,49(2):221-240.
[11] Chen F L,Huang H J.A Synthetic Control Chart
for Monitoring Process Dispersion with Sample Range[J].The International Journal of Advanced Manufacturing Technology,2005,26(7):842-851.[12] Davis R B.Woodall.Evaluating and Improving the Synthetic Control Chart[J].Journal of Quality Technology,2002,34(2):200-208.
[13] Wu Z,Spedding.A Synthetic Control Chart for De
tecting Small Shifts in the Process Mean[J].Journal of Quality Technology,2000,32(1):32-38.[14] Wu Z,Yeo S H.Implementing Synthetic Control Charts for Attributes[J].Journal of Quality Technology,2001,33(1):112-114.
[15] Scariano S M,Calzada M E.A Note on the Lower-sided Synthetic Chart for Expnoentials[J].Quality Enginerring,2003,15(4):677-680.
[16] Calzada M E,Scariano S M.The Robustness of the Synthetic Control Chart to Non-nomality[J].Communications in Statistics-Simulation and Computation,2001,30(2):311-326.
[17] Costa A F B,Rahim M A.A Synthetic Control Chart for Monitoring the Process Mean and Variance[J].Journal of Quality in Maintenance Engineering,2006,12(1):81-88.

