基于广义信息熵测度的制造过程质量评估
张根保 曾海峰 王国强 张家为
重庆大学,重庆,400030
0 引言
制造过程是产品质量形成过程中的重要环节,在确认产品设计质量的前提下,它是实现产品设计质量的关键。从信息论的角度看,制造过程的复杂性是指描述制造过程状态所预期需要的信息量。复杂性的程度称为复杂度,制造过程的复杂度越大,表明不确定性和不可预测性越大,进行过程建模所需的信息就越多[1]。目前,国内外对制造复杂性的研究主要集中于生产运营层面,如生产调度、企业物流及资源分配等[2-6],文献[7-9]从人因工程的角度分析了制造过程的复杂性,文献[10]研究了复杂产品的装配决策问题,提出通过防差错设计的装配规划等来降低复杂性,但这些研究未能对造成复杂性的根本原因进行解释和分析,而且很少系统分析制造过程的复杂性对质量控制的影响。
为保证产品制造质量,必须了解复杂性对制造过程的影响、控制过程向随机性演化的趋势。过程运行复杂性行为与开放系统的熵变特性是一致的,根据耗散理论,制造系统的有序结构是在非平衡条件下通过物流、信息流和控制流的作用得以维持的[11]。信息熵与过程有序度之间存在一定的关系,即过程的信息熵大,其有序程度低;反之,过程的有序程度高,则其熵小。这样,通过分析信息熵的变化,然后利用复杂度与过程有序度的关系,就可以用动态复杂度来描述系统的质量状态和演化方向。应对制造过程中的复杂性策略可以分为两种:一种是尽量避免、降低和消除制造过程的复杂性;另一种是理解和管理复杂性,通过对制造过程的定量描述和定性分析,预测和控制过程的质量[12-13]。然而无论采用哪种策略,都必须理解和衡量过程的复杂性。
为定量描述制造系统中的复杂性现象,本文对信息熵理论进行扩展,建立基于规模、难度和状态多样性的广义信息熵模型,然后按照复杂性对时间的依赖关系,将制造过程的复杂性分解为静态复杂性和动态复杂性,利用广义信息熵模型来研究制造过程复杂性的测度方法,并将其用于过程质量控制评估,从复杂性的角度给出过程质量控制有效性的定量测度方法。
1 复杂性的测度
1.1 信息熵的基本概念
在物理学中,熵是表征系统运动混乱程度或系统状态数量丰富程度的物理量;而在信息论中,熵又能描述系统的不确定性和复杂程度。制造系统作为复杂开放系统,每个确定的系统状态都对应着一种有序的要素结构,系统状态的转移意味着一种新的有序结构的出现[14]。按照信息论对熵的定义,设离散型随机变量X具有n种可能的取值 (x1,x2,…,xn),且各值的概率分别为 (p1,p2,…,pn),则 X 的熵定义为[13,15]
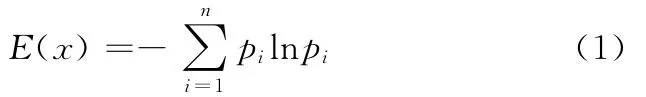
1.2 复杂性测度的广义信息熵模型
仅依照信息熵描述复杂度,难以完整表达制造过程中的规模复杂性现象(如特征、工序的数目等),而忽略规模复杂性显然与实际情况不符,标准信息熵模型的另一个缺陷是无法充分利用设计、制造、工艺人员的经验信息。为此根据制造系统的特点,参照文献[7]的复杂度模型,从数量、多样性和相对难度三个方面考虑,建立复杂性测度的广义信息熵模型(extended information entropy model,EIEM),如图1所示。其中数量或规模造成的复杂性要素为

式中,N为对象规模或数量。

图1 复杂性测度的广义信息熵模型
状态多样性造成的复杂性要素采用下式计算:

式(3)中pi由对象的状态划分确定。本研究将过程/工步划分为正常或特定异常,对于有n种状态的工步PS,异常状态种类为n-1,即将对象 划 分 为 PSSn,PSS1,PSS2,…,PSSi,…,PSSn-1,其中PSSn表示正常状态,PSS1,PSS2,…,PSSn-1为特定异常状态。PSSi概率的具体值pi由工步在该状态下持续的时间TPSSi确定,为便于计算,要求按照异常状态的主因对工步状态进行明确的划分,即在特定时间工步的状态属性必须是唯一的,于是pi=TPSSi/T,其中T为工步PS的总持续时间。
实现难度造成的复杂性用难度系数KC表示,如工序的复杂性随其实现难度的增加而增加。KC具有主观性和和模糊性的特点,因此需采用模糊评价、灰色评价等描述不确定性属性的方法计算。
本文采用三角模糊数进行评判,计算过程中综合运用模糊集理论和层次分析法,以三角模糊数代替常规层次分析法中的标度,确定KC的实现难度。KC的评价步骤如下:①确定评价人员或评价小组,确定待评的过程/工序,建立实现难度评价的层次模型;②确定三角模糊评语等级;③建立模糊判断矩阵;④计算各过程/工序在隶属于同一准则的各考核指标下的实现难度评价分值;⑤计算在各准则及总目标下的评价结果向量,根据计算结果获得各过程/工序实现难度的评价向量,具体计算过程参见文献[16-17]。
根据以上方法获得的实现难度为相对实现难度,对特定过程/工序/工步的质量评估,可以直接运用相对实现难度计算,此时隐含假设难度最小的过程为标准过程,并以模糊评价相对难度系数作为实现难度。如果要利用本方法对多个制造过程进行质量比较,需计算绝对实现难度,此时只需确定某过程的实现难度为标准过程难度,通过与相对难度系数对比,就可求出以标准过程难度为基准的各过程的绝对实现难度。
结合以上三个要素,复杂性测度的广义信息熵模型为

式(4)不但能够捕捉对象状态变化造成的动态复杂性,而且表达了对象规模造成的复杂性,比单独采用信息熵模型或组合规模复杂性模型更符合制造过程复杂性的实际情况。同时,式(4)通过H和DR从客观角度衡量对象的复杂性,通过KC从主观的角度搜集设计、制造、工艺人员的经验信息,其测度要素比单纯依赖主观评估的复杂性度量模型更全面。
2 制造过程的复杂性测度
2.1 制造过程的复杂度
制造过程的复杂度与产品的需求密切相关[1],产品制造需满足设计要求,因此工件的材料、加工工序、设备类别、夹具、检验量具、运行模式等影响制造过程的因素都可能造成复杂性。按照复杂性的来源和特点,我们将这些要素归为工艺复杂性、过程复杂性及由两者造成的系统宏观运行复杂性三类,三类复杂性之间的关系如图2所示。
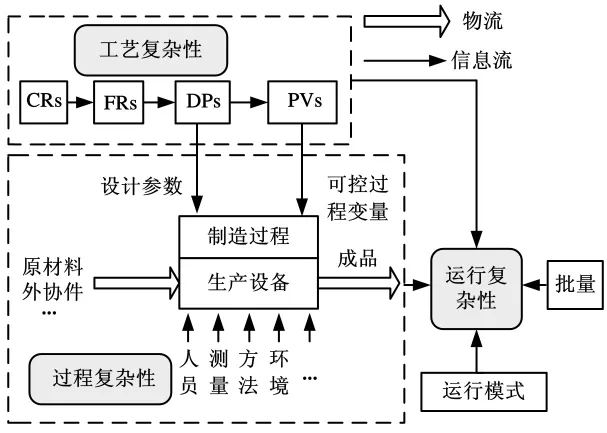
图2 制造系统复杂性分解
工艺复杂性在设计过程中产生,同样功能的产品,如果工艺方案不同,制造过程的复杂性也不同,因此需考虑从顾客需求 (CRs)→功能需求(FRs)→设计参数(DPs)→过程变量(PVs)各转化过程;过程复杂性描述将DPs转化为实际物理特征中的不确定性,因此过程复杂性应涵盖了制造资源约束下的工序能力及制造过程中5M1E产生的随机影响;运行复杂性主要关注系统宏观上是否按预定的调度计划运行,如果系统按预计的调度计划生产运行,制造系统的运行复杂性保持不变,系统处于受控状态,当系统的内外环境的变化导致调度计划与实际状态偏离时(如临时产品的加工、设备故障、调整运行模式等),系统运行复杂性增加[13]。
制造过程的复杂性就是产生于这些要素的多样性和不确定性,为便于利用复杂性测度的广义信息熵模型描述制造过程的复杂行为,按照对时间的依赖性把过程复杂性分为静态复杂性及动态复杂性。定义加工过程为P= {P1,P2,…,Pi,…,Pcn},Pi= {PSi1,PSi2,…,PSij,…,PSici},PSij={PSSij1,PSSij2,…,PSSijk,…,PSSijcij},其中Pi为加工过程的第i道工序,PSij为工序Pi的第j道工步,PSSijk为工步PSij的第k个状态,cn为工件加工所需的工序数目,ci为工序Pi所含工步数目,cij为工步PSij的状态数目。
2.2 制造过程静态复杂度
过程的静态复杂度是描述制造过程预期状态所需要的信息量,用CS表示。CS主要由工艺方案及实现工艺方案所涉及的制造资源决定,不随时间变化。文献[1]把来源于多可选加工设备和多加工路线造成的复杂性称为虚拟复杂性(imaginary complexity),其实质是资源的组合优化问题,一般采用遗传算法、蚁群算法、免疫算法来解决[18]。虚拟复杂度在产品的加工方案、工艺流程确定之后降为0,此时加工设备及路线都是确定的,因此过程静态复杂度不需要考虑虚拟复杂性。根据复杂性测度的广义信息熵模型,制造过程静态复杂性的数量要素Hi直接通过工步数目计算:

根据式(3),制造过程中工步PSij的静态多样性要素:
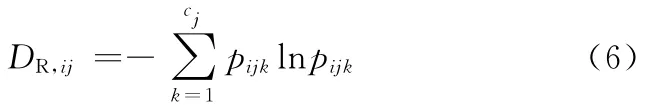
式中,pijk为工步PSij第k个状态的概率。
根据式(2)~ 式(4),工序Pi的静态复杂度表达式为
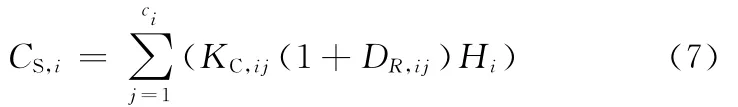
综合式(5)~式(7),工件制造过程的静态复杂度为
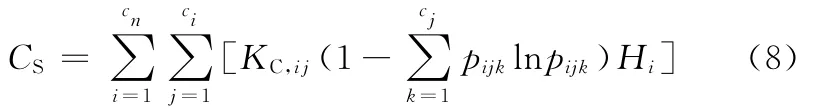
过程的观测尺度对CS的值影响较大,而观测尺度取决于对系统的关注点及可操作性等方面的考虑。为了便于比较和分析,对离散制造系统,取工步作为最小观测尺度,工步内或更小尺度上的状态变化不计入复杂性度量范畴。当然,根据分析需要也可以设置更大或更小的观察尺度,如分析水轮机、船用主轴这类大型工件的加工过程时就需进一步细分,以便考察和分析工步内的复杂性规律。
KC,ij采用模糊评价确定,评价指标主要有材料的可加工性、设备的加工能力、产品特征的工艺性、质量要求、质量检验难度等。评价决策人员由来自设计、工艺和制造部门组成,以综合利用这些人员的经验信息。
理想条件下制造过程各工步的预期状态为设计期望,因此静态过程为确定状态系统,DR,ij=0。工艺设计方案在本质上决定了数量要素Hi和难度系数KC,ij,从而确定了系统的静态复杂度。
2.3 制造过程的动态复杂度
静态复杂度只考虑产品制造的期望状态,而动态复杂性则需要进一步关注制造过程中实际发生的状态,即制造过程中的状态不确定性。制造过程在运行中的实际状态由过程检测或状态监测获得,当加工状态偏离期望时,系统的熵增加,对任意工序Pi,其动态复杂度由下式计算:
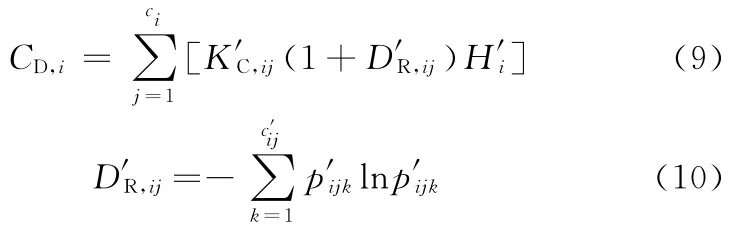
综合式(9)、式(10),工件制造过程的动态复杂度为

其中,D′R,ij为工步PSij的动态多样性要素,K′C,ij为PSij的动态难度系数,H′i为Pi的动态数量复杂性要素,D′R,ij为动态多样性要素,c′n为实际加工中所用的工序数目,c′i为实际加工中工序Pi所含工步数目,c′ij为实际加工中工步PSij的状态数目,p′ijk为工步PSij处于第k个状态的概率,在加工期间如果工艺设计方案不变,则K′C,ij= KC,ij,H′i= Hi,否则需重新评估。
如果加工过程保持在期望状态,则D′R,ij=DR,ij。实际上,由于受到人员、设备、材料、外界环境等因素的随机影响,加工状态是围绕期望状态波动的,因此D′R,ij>DR,ij。设工步PSij的状态数目为c′ij,其期望状态概率为p′ij1,则其他状态数目为c′ij-1,且有
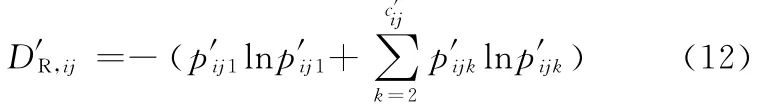
状态发生变化并不意味着发生故障,如为了保证加工精度而定期对夹具、刀具进行必要的调整,这种加工状态的变化就不属于故障状态。但是由于这种调整打断了正常的加工,同样增加了复杂度,因此状态复杂度又可表示为
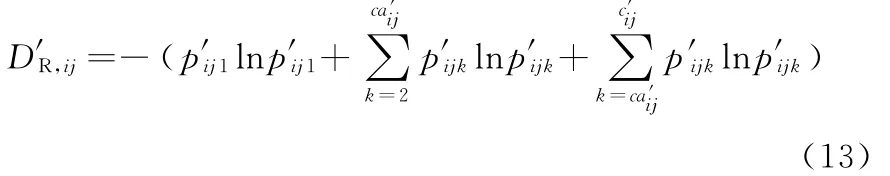
其中,ca′ij为工步PSij调整后正常状态的数目,工步PSij故障状态的数目为cij-ca′ij-1。为便于比较,与静态复杂性一致,D′R,ij同样取工步为最小观测尺度,状态发生的概率根据实际统计数据确定。当以工步为最小观测尺度时,如果调整未打断正常加工工序,则调整不计入状态复杂性,如机床的自动补偿。
3 基于复杂度的过程质量评估
3.1 过程质量的有效性评估
过程质量的有效性是指过程控制达到预期结果的程度。根据AD信息公理,信息量最小的过程,制造的产品满足设计要求的概率最大,因此可以利用静态复杂性和达到质量控制要求时的动态工序复杂性对过程质量的有效性进行描述。加工过程由于受到各种随机因素的扰动,不可避免地会发生偏离,但工序的K′C,ij和H′i不变,所以动态复杂性的变化主要来源于D′R,ij,根据式(13),D′R,ij的变化又可以分为两种类型:
类型1 在出现异常前主动中断工序进行调整,调整后工件质量符合要求,此时D′R,ij的第二增大。这种情况增加了加工过程的复杂度,但是加工状态的变化属于质量控制下的调整,因此有利于质量控制有效性的维持和改进。
类型2 在发生状态异常,工件加工质量不符合要求时中断工序,则此时D′R,ij的第三项增大,这类复杂性除了造成生产中断外,还导致返工和废品等,破坏了工序的有效性。
D′R,ij发生类型1的变化说明企业已经掌握了工序变化的信息和规律,并且能够利用这些信息进行工序调整。但必须注意的是,过度频繁地中断生产进行工序调整将增大加工成本,而且这种调整对工序质量控制的改进是有极限的,因此需设定合理地调整周期以保证成本和质量的最佳平衡。当D′R,ij变化源于类型二变化时,如果状态异常造成的质量异常超过规定比例,则说明工序能力过低,必须进行工序改进。
根据以上分析,质量控制的动态有效性可用下式评估:
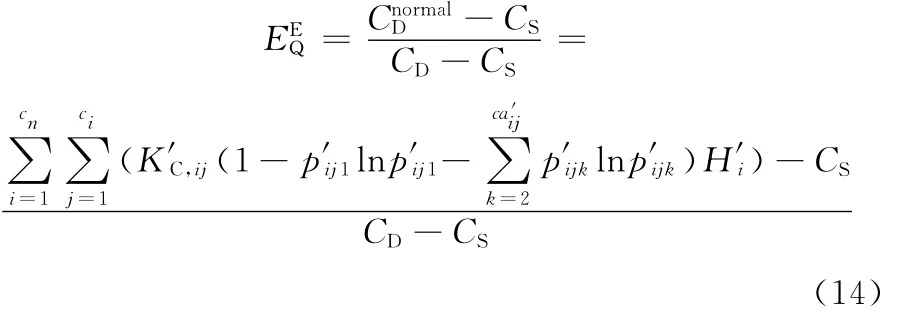
其中CnormalD为工件加工质量正常情况下的复杂度,计算方法参见式(9)~ 式(13)。
过程的动静态复杂度的一致性反映了加工过程在内外部环境扰动条件下,保持稳定的加工质量的能力,可作为过程健壮性评估指标,通过下式计算:

如果加工过程的两个类型的状态多样性水平都很低,表明过程的抗扰动能力相对较强,在无需过多过程维护的情况下也能保证加工质量和较低的故障水平。
利用基于复杂度的定量分析对现行质量控制方案进行评估,则可以帮助企业分析控制方案的有效性,深入分析造成复杂性的原因,找出质量改进的方向和途径。
3.2 基于复杂度的质量监测
为保证产品制造质量,需监测制造过程的动态变化,控制过程向随机性演化的趋势。通过监测C′D的平均变动,然后利用复杂度与过程有序度的关系,就可以用动态复杂度来描述过程的质量状态和演化方向。设从t0开始,以Δt为统计周期对加工过程进行监测(Δt大于最小观测尺度),则t1时的过程复杂度为,可根据式(9)计算,因此动态复杂度在t0-t1期间的相对平均变动为
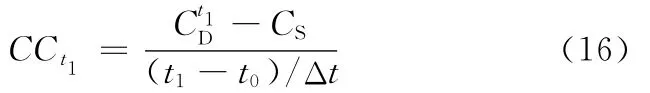
通过对复杂度变化的持续监测,得CCt={CCt1,CCt2,CCti,…},根据这些数据就可判断过程有序度的变化,从而估计质量的状态和变化趋势。
4 案例研究
某企业的齿轮加工过程包括毛坯粗加工、半精加工及精加工等7道工序,23道工步。齿轮具体参数如下:模数m=2.25mm,齿数z=50,压力角α=20°,螺旋角β=20°,毛坯为45钢,毛坯外形尺寸为φ121mm×68mm,其他参数如图3所示。工序10到工序40采用CA6140车床加工,三爪自定心卡盘定位。滚齿工序50采用Y3150加工,芯轴定位。工序60采用X6132铣床加工。
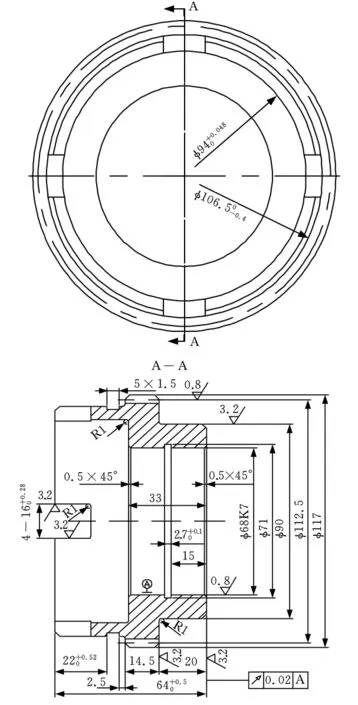
图3 车床齿轮零件图
4.1 齿轮加工过程的静态复杂度
首先确定齿轮加工的数量复杂性和难度复杂性要素。数量复杂性要素根据齿轮加工的工步数目确定,表1列出了齿轮加工的主要工序、工步及其内容以及一些参数。难度系数通过模糊决策方法确定,评价决策人员来自于设计、工艺和制造部门。在静态复杂度计算之前,先用Grubbs检验法对可疑数据进行检测,剔除异常值和粗大误差数据,保证数据的一致性和可用性。表1直接给出评估结果(KC列),根据式(8),齿轮加工过程的静态复杂度为14.03。
4.2 齿轮加工过程的动态复杂度
为简化计算,本算例假设加工期间工艺设计方案不变,因此动静态数量复杂性和难度复杂性要素相同(表1中 H 和KC列),即K′C,ij=KC,ij,H′i= Hi。本例观察周期Δt取40h(5×8h),表1中第5列和第6列分别为在出现异常前主动中断工序进行调整的概率和加工质量异常中断工序的概率。由于篇幅关系未列出具体各状态类别和具体数据,只给出这两类类型发生的总概率。下面以滚齿工序为例,给出两类状态多样性的计算方法。

表1 齿轮加工工艺及复杂度算例
滚齿工序在观察周期内,工作正常的概率p′ij1=2200/(40×60)=0.917;定时进行滚齿机刀具检查耗时100min,p′ij2=100/(40×60)=0.042;因齿向误差超差,调整压紧螺母和垫片耗时40min,p′ij3=0.017;因为滚刀崩刀导致加工的轮齿表面同一部位产生纵向的沟纹,通过轴向窜动滚刀解决,耗时60min,p′ij4=0.025,根据式(13),可知D′R,50,1=0.3726。其他各工序D′R,ij计算方法类似,计算结果见表1中第9列。根据式(11),计算得最终动态复杂度为15.9864。
4.3 齿轮加工过程质量控制的有效性评估
加工过程质量控制的有效性按照式(14)评估:

这说明过程中的动态复杂度中有63.17%是过程正常状态下产生的,其余复杂性由过程异常导致,为无效复杂性。进一步对表1第6列状态概率进行具体数据分析,发现镗孔工步10-5和滚齿工步50-1为造成异常类复杂性的重要原因。
根据式(15),过程的静动态复杂度的一致性指标为
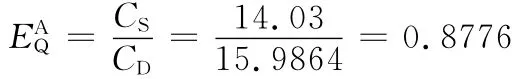
齿轮加工过程的静动态复杂度的一致性不高,为0.8776,说明过程的健壮性不高,为保证加工质量,加工过程中不得不进行大量调整和维护活动。
结合上述指标EEQ和EAQ分析,由于齿轮加工过程健壮性差,导致过程的抗扰动能力相对比较弱,因此必须依赖过程调整和维护活动保证工件加工质量。这种做法虽然保证了产品的质量水平,但是质量成本较高。必须找出提高过程稳健性的措施才能从根本上提高过程质量。对表1数据进行分析,我们提出如下改进措施:改进齿轮的毛坯加工和热处理工艺以提高毛坯精度,同时校准滚齿机,并强化齿轮加工规程。
根据式(16)计算平均动态复杂度,实施质量改进措施后持续监测平均动态复杂度8周,图4为基于复杂度的质量监测图,质量改进后平均复杂度从1.96下降到1.41,相比未改进前降低28%,同时加工合格率从79.6% 提高到97%。为从统计上检测质量改进的显著性,对质量改进前后合格率、平均复杂度进行假设检验。

图4 基于复杂度的齿轮加工过程质量监测图
取改进前后各8周的数据,利用配对样本(d1,d2,…,d8)来检验,di=Xi-Yi,Xi、Yi分别为质量改进前后的合格率\平均复杂度。配对样本可以看作是来自正态总体N(d,σ20+σ21)的样本,此时σ0≠σ1,n0=n1,对于平均复杂度,检验假设H0:d=0,H1:d>0,由于方差σ20+σ21未知,绝域为T>tα(n-1)。经计算得平均复杂度tco=tα(n-1)=t0.01(7)= 2 .9998,tco= 1 4.25 >2.9998,故拒绝H0,即认为平均复杂度显著降低。同理,计算得合格率tcf=15.6>2.9998,故认为改进后合格率得到显著提高。可见与质量改进前相比,质量改进措施有效降低了齿轮加工过程的复杂度,提高了合格率。
本案例利用广义信息熵模型对齿轮加工质量进行了评估。评估综合了数量要素、实现难度和状态多样性要素造成的复杂性,比单纯采用信息熵模型、规模复杂性模型或主观评价模型更为全面。
从本案例可以看出,通过广义信息熵模型的过程数量复杂性和难度复杂性要素,可以进行制造过程静态评估。本例中齿轮加工过程的静态复杂度评估值为14.03,而单独采用信息熵模型,无法进行制造过程的静态复杂性评估;广义信息熵模型通过纳入状态多样性要素,实现对齿轮加工过程质量评估的动态化。例如,在实施质量改进措施后,制造过程的平均复杂度从1.96下降到1.41,而规模复杂性模型在产品的设计方案和工艺方案确定以后就不再变化,是一种静态评估模型,无法体现制造过程中质量状态的改变;主观评价模型由于一般不进行动态评价,因而也无法对两次之间制造过程质量的变化作出响应,而广义信息熵模型中将实现难度的评价值以加权系数的形式处理,在综合设计、制造、工艺人员主观经验信息的同时,避免了无法进行动态制造过程质量评估的问题。
5 结束语
过程控制是产品制造质量控制的重要方法,制造过程中的复杂性导致过程建模、预测和控制困难。为保证产品制造质量,必须了解复杂性对制造过程的影响,控制过程向随机性演化的趋势。制造过程中的信息熵与其复杂度成反比关系。为定量测度制造过程中的复杂性,本文对信息熵理论进行扩展,建立了基于规模、难度和状态多样性的广义信息熵模型;然后提出利用此复杂性测度模型,进行制造过程静态和动态复杂度的测度方法,并将其用于制造过程质量控制评估,从复杂性的角度给出了过程质量控制有效性的定量评价方法;最后通过实例展示了该理论和方法的有效性。需注意的是,熵量计算是一种宏观定性方法,通过广义信息熵的测度实现制造过程复杂性的量化,是针对复杂制造过程的一种间接评估方法。对制造过程中可直接量化的过程质量特性,采取质量统计方法评价更为简洁和准确。本文提出的复杂性测度理论和方法为描述和分析制造过程提供了一个新的视角和方法,可应用于制造系统可靠性、健壮性等其他方面的分析。
[1] Nam S.Axiomatic Design:Advances and Applications(the Oxford Series on Advanced Manufacturing)[M].London:Oxford University Press,2001.
[2] 姚倡锋,张定华,彭文利,等.面向复杂零件网络化制造的资源优化配置方法[J].计算机集成制造系统,2006,12(7):1060-1067.
[3] 吴正刚,韩玉启,宋华明,等.复杂产品的模块化制造战略研究[J].中国机械工程,2005,16(20):1826-1830.
[4] Cho S,Alamoudi R,Asfour S.Interaction-based Complexity Measure of Manufacturing Systems Using Information Entropy[J].International Journal of Computer Integrated Manufacturing,2009,22(10):909-922.
[5] Papakostas N,Efthymiou K,Mourtzis D,et al.Modelling the Complexity of Manufacturing Systems Using Nonlinear Dynamics Approaches[J].Cirp Annals-manufacturing Technology,2009,58(1):437-440.
[6] Siemieniuch C E,Sinclair M A.On Complexity,Process Ownership and Organisational Learning in Manufacturing Organisations,from an Ergonomics Perspective[J].Applied Ergonomics,2002,33(5):449-462.
[7] Eimaraghy W H,Urbanic R J.Modelling of Manufacturing Systems Complexity[J].CIRP Annalsmanufacturing Technology,2003,52(1):363-366.
[8] Eimaraghy W H,Urbanic R J.Assessment of Manufacturing Operational Complexity [J].CIRP Annals-manufacturing Technology,2004,53(1):401-406.
[9] Eimaraghy W H,Urbanic R J.Modelling of Manufacturing Process Complexity[J].CIRP Annalsmanufacturing Technology,2003,52(1):363-366.
[10] Zhu X W,Hu S J.Karen Y,et al.Modeling of Manufacturing Complexity in Mixed-model Assembly Lines[J].Journal of Manufacturing Science and Engineering-transactions of the Asme,2008,130(5):1-10.
[11] 尹晓虎,钱彦岭,杨拥民,等.基于熵的装备维修系统效能评估与仿真[J].系统仿真学报,2008,20(16):4404-4407.
[12] Efstathiou J.The Utility of Complexity[J].Manufacturing Engineer,2002,81(2):73-76.
[13] 饶运清,Efstathiou J.基于信息熵的制造系统复杂性测度及其在调度中的应用[J].机械工程学报,2006,42(7):8-13.
[14] 汪泽焱,益晓新.基于基点和熵的系统评价指标赋权法[J].解放军理工大学学报,2002,3(3):91-95.
[15] 张志峰.离散制造企业生产物流的熵模型评价及其应用[D].武汉:华中科技大学,2008.
[16] 姬东朝,宋笔锋,喻天翔.模糊层次分析法及其在设计方案选优中的应用[J].系统工程与电子技,2006(11):1692-1694.
[17] 曹柬,周根贵.一种新的敏捷虚拟企业合作伙伴选择与评价方法[J].中国机械工程,2004,15(22):2009-2013.
[18] 刘金山,廖文和,郭宇.基于双链遗传算法的网络化制造资源优化配置[J].机械工程学报,2008,44(2):189-195.

