点啮合齿面CNC制造技术的曲面包络逼近法
周凯红 周晓艳
桂林航天工业高等专科学校,桂林,541004
0 引言
准双曲面齿轮副齿面是一种满足高速重载动力传动要求的点啮合齿面,它的啮合性能由啮合点处两齿面的几何结构确定。基于传统摇台式机床的格里森齿面展成技术不能控制两齿面啮合迹线上每一个啮合点处的几何结构,无法保证加工齿面的啮合性能。基于计算机数字控制技术的Free-Form型多轴联动数控机床的出现为改变这种状况提供了可能。但基于该技术的齿面展成方法是,通过对刀具与工件在展成参考点处的相对空间位置和运动进行等效转换,直接将传统摇台机床加工准双曲面齿轮的原理和方法运用于Free-Form型机床。这种方法的实质是以数控机床模拟传统摇台机床的功能,没有充分发挥Free-Form型机床万能运动的特点,无法加工优化设计的啮合特性预定的点啮合齿面[1-2]。Litvin等[3]通过展成一个与目标齿面沿一给定的曲线相切的近似曲面,并以该曲面按一个给定的目标函数逼近目标齿面来确定刀具与工件的相对位置和相对运动即机床加工调整参数。该方法只能部分满足齿面预定的啮合性能要求[4]。与上述两种材料线去除齿面加工方法不同,文献[5]将点啮合齿面视为一般的自由曲面,在通用数控机床上以具有自适应性法矢的球面作为加工刀具,按给定的刀具轨迹规划完成齿面的加工。该方法的缺陷是,其材料去除方式是点去除,加工效率低,但从理论上说它能精确加工任何设计齿面。该方法主要用于大模数齿轮和齿轮模具的加工。
本文提出了在内蕴齿面微分几何特性的曲面活动标架下确定刀具相对工件展成运动的新方法,按此方法加工得到的齿面在指定的接触迹线附近与目标齿面有二阶切触,并能通过改变刀具在展成目标齿面上指定接触迹线各点时的姿态,使刀具的包络面的其他区域以最小偏差逼近目标齿面。这就是所谓展成点啮合齿面的包络逼近原理。本文所提出的这种齿面展成方法可以在Free-Form型五轴联动的数控机床上展成按预定啮合特性设计的点啮合齿面。
1 点啮合齿面展成运动的曲面活动标架描述方法
点啮合齿面的啮合特性由两啮合齿面接触迹线上每一个啮合点处的零至二阶参数以及接触迹线以外两啮合齿面的间隙确定。基于数控技术加工具有预定啮合特性的点啮合齿面就是控制刀具相对工件的运动,使刀具曲面在此运动下的包络面与加工目标齿面沿齿面接触迹线具有二阶切触,而在接触迹线以外的区域,包络面按预定的(最小)偏差逼近加工目标曲面。因此,展成齿面的刀具相对工件的运动应按加工目标齿面的几何结构来控制和描述。
活动标架的概念起源于研究刚体运动。Darboux等[6]以空间曲线的Frenet标架沿曲线的运动来研究空间曲线的微分结构。Cartan将活动标架引入空间曲面的研究,又将其从运动群推广到任意李群,并引进外微分形式,形成研究曲面微分结构的新方法[7]。这一新方法的特点是将曲面微分特性与标架沿曲面的运动联系起来,特别适合描述和控制刀具展成复杂曲面的相对运动。
如图1所示,刀具曲面Σt通过相对于坐标系Sp{Op;xp,yp,zp}的运动Ψ 包络出曲面Σg。设Lp是曲面Σg上的一条曲线,Lt是曲面Σt上的一条曲线,Lp与Lt对于运动Ψ相互共轭。Lg是形成包络曲面Σg的特征线。因此,在运动的任意时刻,曲面Σt与Σg相切于Lg,而Lg总与Lt和Lp三线交于点M,故在点M,对于曲面Σt与Σg分别有活动标架Sft{M;αt,υt,nt}和Sfp{M;αp,υp,np}。其中,αi(i=t,p)是曲线Li在点M 的单位切矢,ni是曲面Σ(i)在点M 的单位法矢,υi=ni×αi。加工目标齿面Σp与曲面Σg固结且沿曲线Lp与曲面Σg具有二阶切触,即曲面Σg和齿面Σp沿曲线Lp二阶及二阶以下参数均相等。
曲面Σt相对曲面Σg的角速度为

图1 基于曲面活动标架的齿面展成运动模型
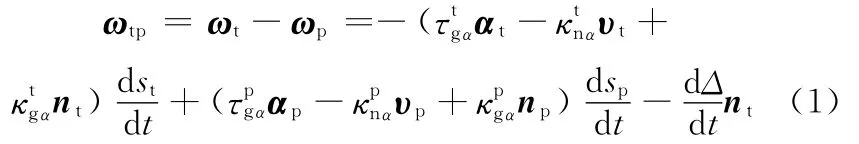
在M点,曲面Σt相对曲面Σg的速度为
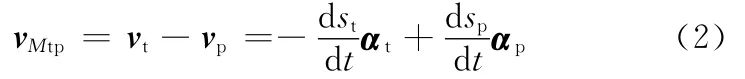
因此,在任意点P,曲面Σt相对曲面Σg的速度为

于是,曲面Σt的包络运动Ψ被表示为曲面Σt和Σg及其各自曲面上的曲线的微分几何(活动标架运动)参数及两曲面活动标架的相对位置参数的函数。
2 展成点啮合齿面的包络逼近原理
实际上,运动Ψ也代表一种从曲面Σt到曲面Σg的运动变换。如果曲面Σt是一种曲面结构比较简单的刀具曲面(如平面、圆柱面、圆锥面和各种螺旋面等),那么,通过控制这种变换就可能包络出结构复杂的曲面Σg使其以最小的误差逼近一个加工目标曲面。这就是包络逼近原理。
2.1 加工目标齿面Σp和刀具曲面Σt及坐标系
这里的加工目标齿面Σp及其上指定曲线Lm就是按预定啮合特性设计的点啮合齿面和其上的接触迹线,它在展成运动中始终与坐标系Opxpypzp固结。因为它是要求加工的目标齿面,所以,目标齿面Σp和指定的接触迹线Lm的方程是已知的,设其在坐标系Opxpypzp中可以分别表示为
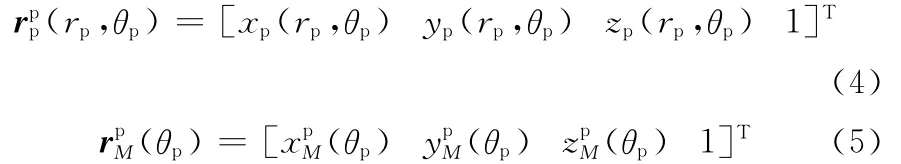
接触迹线Lm的切矢为

刀具曲面就是传统的标准刀盘,它是一个圆锥面,切齿刀盘与坐标系Otxtytzt固结(图2),它的参数方程在此坐标系中为

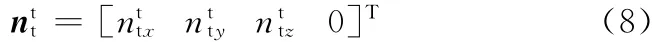
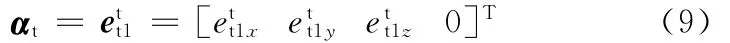
另一个主方向(沿圆锥准线)单位矢量为

图2 刀具曲面及其坐标系

刀具曲面Σt上展成目标齿面Σp上的接触迹线Lm的刀刃线Lt即圆锥面的一条母线Ln(图2)。
2.2 刀具包络面Σg和目标齿面Σp沿接触迹线Lm的二阶切触条件
设M处沿接触线Lg的方向为Ig,M处沿Σp上的指定的曲线Lm的方向为Im(即Lm在点M的切线幺矢ep的方向)(i=t,p;j=1,2)分别表示刀具曲面Σt和目标齿面Σp在M处的主方向(图3),那么,沿方向Ig,曲面Σt与曲面Σg的法曲率和短程挠率相等,即


图3 由二阶插值条件确定位置参数Δ
由于要求刀具曲面Σt所展成的曲面Σg与目标齿面Σp沿指定曲线Lm具有二阶切触,故在M点,曲面Σg与Σp具有相同的主方向和对应相等的主曲率,即

故由欧拉-贝特朗公式可求得
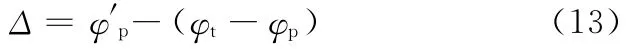
由式(11)~式(13)可将Δ表示为参数rtM和θp的函数。其中,rtM是点M 在曲面Σt上的啮合点到Σt的锥顶的距离。由于曲面Σt是锥面,当Σt沿锥面母线相对Σp移动(即rtM改变)时,Σt的包络曲面Σg总能与目标齿面Σp沿指定的曲线Lm具有二阶切触。但对于不同的rtM值,Σg在曲线Lm以外的区域逼近目标齿面Σp的程度是不同的,因此,可以通过控制rtM的变化,使Σg在曲线Lm以外的区域充分逼近目标齿面Σp来控制刀具加工出满足设计要求的齿面。
2.3 刀具曲面Σt及其包络曲面Σg在坐标系Sft中的啮合方程
刀具曲面Σt及其包络曲面Σg在坐标系Sft中的啮合方程可写为
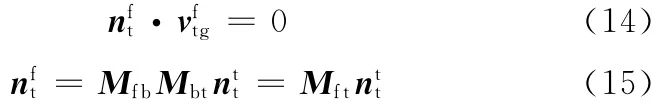
式中,Mfb为坐标系Sft到坐标系Sfp的变换矩阵(图1);Mbt为坐标系Otxtytzt到坐标系Sft{M:et1,et2,nt}的变换矩阵(图2);Mft为坐标系Otxtytzt到坐标系Sfp的变换矩阵(图2)。
将式(3)、式(15)代入式(14),将式(14)在坐标系Sft中写成齐次坐标的形式,并消去dsp/dt得

这里要特别指明的是,式(16)中的rtt是曲面Σt与曲面Σg的接触线Lg上任意点N到曲面Σt锥顶Ot的距离(即向量r的模)(图2)。
2.4 刀具曲面Σt的包络曲面Σg在坐标系Sp中的参数方程
曲面Σg是刀具曲面Σt相对工件运动形成的曲面族的包络面,它在工件固连坐标系Sp中的参数方程为

式(18)中的npp总是指向Σp的实体。
由式(17)可消去参数rtt,故曲面Σg的参数方程可表示为关于θt、θp、rtM和drtM/dθp的参数方程,这个曲面方程中的θp是曲面Σg的独立参数,它表示Σg与Σt接触线的位置。为了在下面曲面Σg与齿面Σp发生关系时,避免与Σp的参数θp混淆,故把这个曲面方程中的θp命名为θg,即
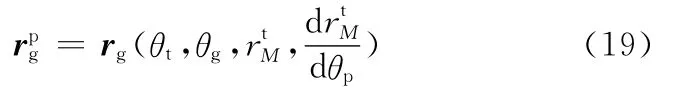
2.5 通过曲面Σg逼近目标齿面Σp确定参数rtM和drtM/dθp
刀具曲面Σt沿接触迹线Lm相对齿面Σp按式(3)运动,在与齿面Σp固连的坐标系下展成曲面族Σg(式(19))。这是一个与齿面Σp在接触迹线Lm附近有二阶切触的曲面族,若以Σg最小偏差逼近目标齿面Σp为条件,可以从此曲面族中优选出一个曲面,从而确定rtM及drtM/dθp,进而由式(13)确定Δ(rtM,θp),最终由式(3)确定刀具与工件之间的相对运动。为此必须建立以曲面Σg与目标齿面Σp偏差距离δ最小为目标的齿面优化模型。

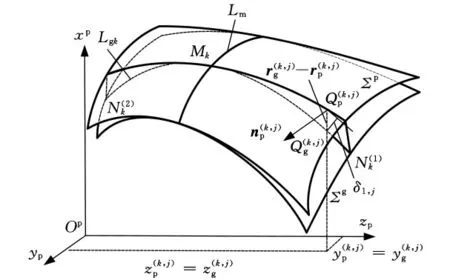
图4 曲面Σg沿接触线Lgk与曲面Σp的偏差的确定
因为要同时控制接触迹线Lm两侧的偏差最小,所以,齿面优化目标是接触迹线两侧的偏差和最小,故曲面逼近的数学模型如下:
目标函数

约束条件

判断Fk是否小于一个设计所要求很小的偏差值ε,若是,则接受上述设计结果;若不是,则应改变刀具曲面Σt的形状,重新按上述方法设计刀具相对工件的运动。一般通过改变Σt的压力角即半锥角α0t或将Σt由锥面改为球面来满足加工要求。
确定与Mk对应的式(15)确定展成 Mk时的Δ,然后,由式(8)、式(12)确定刀具相对工件的运动。这就是由展成齿面的几何结构确定的刀具相对工件的运动方程,它写在坐标系Sfp下。通过坐标系Opxpypzp、Sfp、Sft和Otxtytzt之间的坐标变换矩阵可以将刀具相对工件的运动方程写到坐标系Opxpypzp中,并确定刀具相对工件的位置关系。上述刀具与工件相对运动和相对位置的描述都是在坐标系Opxpypzp、Sfp、Sft和Otxtytzt中进行的(图3、图4),与机床坐标系无关。要在Free-Form型机床上加工上述齿面,必须在Free-Form型机床上等效实现刀具与工件的上述相对运动和相对位置关系。
3 包络逼近原理在Free-Form型机床上的实现
3.1 Free-Form型机床简介
图5是CNC铣齿机的三维概念图。Free-Form型机床将齿轮加工所需的全部运动用六坐标数控轴实现,取消了摇台、刀倾及偏心机构等,它具有六个联动坐标轴:三个平动轴X、Y、Z;三个转动轴A、B、C。六根轴提供六个自由度,可灵活地控制工件与刀具在空间中的位置和运动。在Free-Form型机床上进行加工时,刀具与工件的运动被分解成为X、Y、Z三个方向的直线运动和A、B、C三个回转运动。刀盘轴线与Z轴平行,工件轴线平行于XZ平面。

图5 Free-Form机床的三维概念模型
另外,在Free-Form型机床上,六根数控轴的运动是独立的,但是,只有X、Y、Z三个方向的直线运动和A、B两个回转运动合成工件和刀具之间的展成运动,它们按不同组合进行联动,可以展成不同曲面逼近预先设计的齿面。刀盘轴线C只产生切削力所需的运动,与齿面展成运动无关。
3.2 机床运动分析坐标系
如图6所示,坐标系Otxtytzt和Opxpypzp是分别与刀刃和工件固结的坐标系,其中zt轴和zp轴分别与C轴和A轴重合。Omxmymzm是与机架固结的固定坐标系,Om位于A轴与B轴的交点,它的各坐标轴分别与机床各坐标轴对应平行。坐标系Ohxhyhzh与Omxmymzm的各对应坐标轴相互平行,其坐标原点Oh与坐标系Otxtytzt的坐标原点Ot重合于刀盘锥顶。轴zh与C轴重合。坐标系Oexeyeze相对坐标系Omxmymzm绕轴ym转动,ym与B轴平行。Oe与Om重合,轴ye与轴ym重合。坐标系Odxdydzd的xd轴与xe重合于A轴,其余各坐标轴与Oexeyeze的对应各轴相互平行,其坐标原点Od与Om的距离xmdx为常数。Od与Op重合于工件齿轮的根锥锥顶。

图6 Free-Form型机床运动分析所涉及的坐标系
3.3 机床加工调整参数的确定
在Free-Form型机床上实现包络逼近的实质是,通过图6所示的机床坐标系实现图7所示的与包络逼近等效的坐标变换。这一过程由以下两部分确定。

图7 在Free-Form型机床上实现包络逼近时,从刀具曲面到加工目标曲面的两条等效坐标变换路径
3.3.1 由刀具相对工件的等效运动关系确定机床加工时各控制轴的运动方程
按图5、图6所示的Free-Form型机床结构和坐标系关系,写出刀具和工件在五轴联动下的运动方程,并与式(1)、式(3)描述的方程比较,从而求出各运动轴的运动控制方程。
首先得到A轴的位置控制方程:

其次得到B轴的运动控制方程:

最后得到在机床坐标系Omxmymzm下展成点M处刀具相对工件的的速度为

由式(25)得在坐标系Omxmymzm中刀具锥顶Ot相对坐标原点Oe的运动速度为
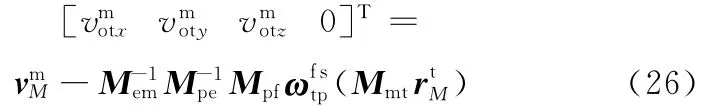
式中,Mem、Mpe、Mpf、Mmt均为坐标变换矩阵(图7)为角速度矢量的坐标方阵。
由式(26)可得机床沿X、Y、Z轴的运动方程。
式(24)、式(26)确定了Free-Form型机床按设计齿面要求加工预定齿面时各数控轴的运动方程,这里,A轴的运动是基准运动。
3.3.2 Free-Form型机床坐标系中刀具与工件相对位置关系的确定
按图5、图6所示的Free-Form型机床结构和坐标系关系,写出刀具和工件在五轴联动下的各机床坐标系的变换矩阵,并与坐标系Opxpypzp、Sfp、Sft和Otxtytzt组成的坐标系变换关系进行比较,从而求出各运动轴的位置控制方程:

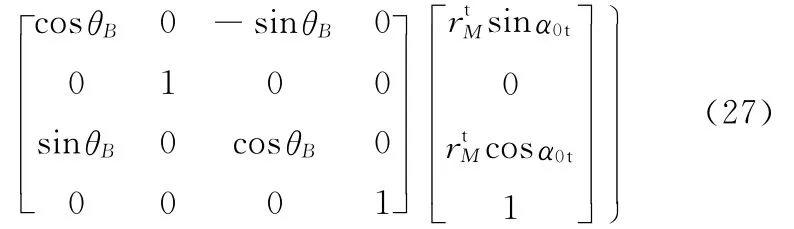
在式(27)中,θA已经由式(23)给出也已经由上节的曲面包络逼近模型确定,因此,在展成M点时,刀具锥面顶点Oh在机床坐标系Omxmymzm的坐标值可以用工件绕B旋转轴相对初始位置转过的角度θB表示。安装距的初始值(展成第一个点时的θB值)确定了展成点在机床坐标系中的位置,因此,可以根据机床结构和展成齿面在机床坐标系中的合理位置来选定θB的初始值,其他展成位置的θB值由式(24)对θp的积分式确定。恰当选择θB的初始值可以优化刀具展成齿面时的切削力。安装距的确定原理与θB的初始值相同。
在按上述方法确定了刀具相对工件的切齿运动和相对位置的控制,并通过五轴联动数控机床实现这些相对运动和五轴位置关系后,接下来要考虑的是齿深控制问题。这里,控制齿深的方法是:在不改变上述刀具与工件相对运动和相对位置关系的情况下,由预先设计的根锥,按啮合原理,对标准圆锥刀盘的刀顶面进行修形(展成),使它们在上述机床运动下与预先设计的根锥共轭,从而切实控制齿深。用这种方法就不必对已经按上述方法设计好的机床调整参数进行修正了。
4 切齿计算实例结果与分析
下面以一弧齿锥齿轮小轮凹面(正车面)的切齿计算为例来验证上述理论推导的正确性。齿轮的基本参数见表1;齿面接触迹线上部分点的一阶和二阶参数见表2。
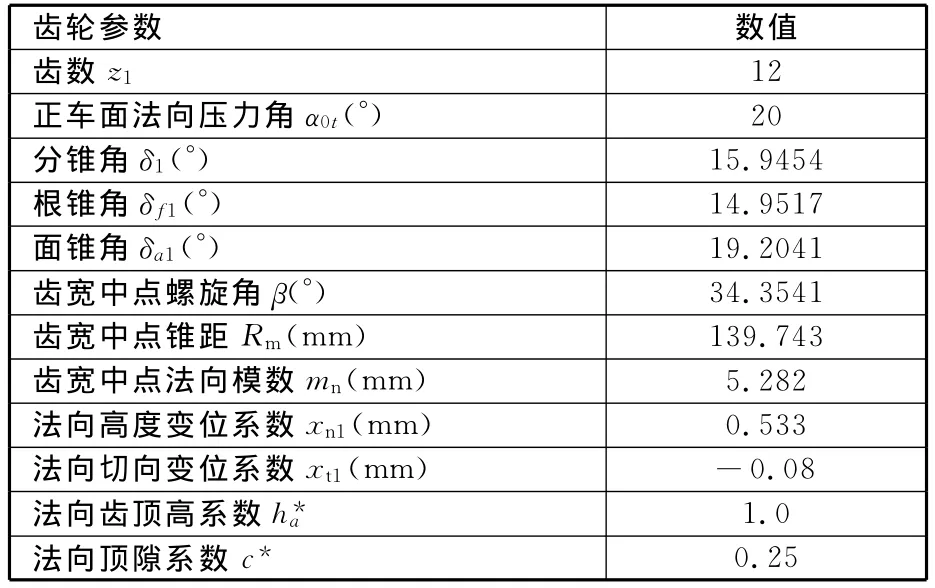
表1 弧齿锥齿轮副小轮主要几何参数表
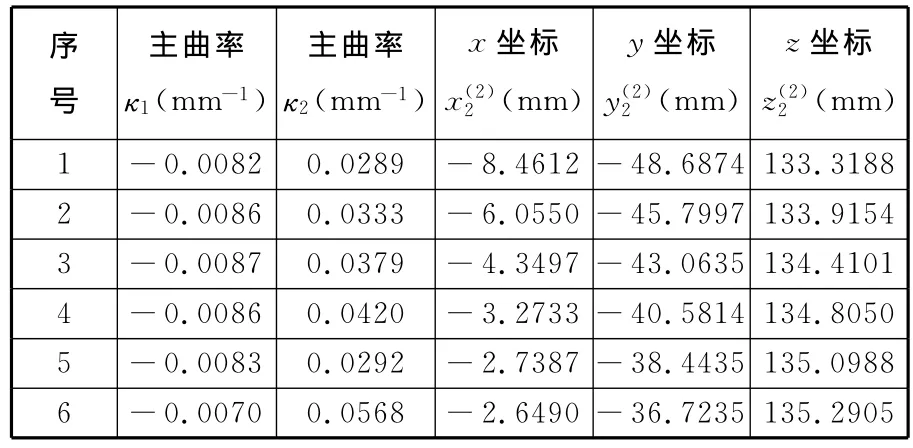
表2 齿面接触迹线上部分点的曲率及坐标
根据本文介绍的切齿加工原理可知:如果不计切齿计算误差和机床加工误差,在加工得到的齿面Σg上,沿指定的接触迹线上各点的零阶、一阶和二阶参数与要求加工的齿面Σp对应各点的零阶、一阶和二阶参数都完全相等,即Σp与Σg沿指定接触迹线具有二阶切触。因此,本文介绍的切齿方法能够加工按预定啮合特性设计的点啮合齿面。表3给出了展成接触迹线上各点的同时,在实际齿面范围内,展成齿面其他区域的最大偏差。图8是按本文介绍方法展成的齿面与理论齿面对照的拓扑修形图。这里的理论齿面是:由给定大轮齿面设计小轮齿面时,大轮按设计所要求的传动规律在工件坐标系中运动得到大轮包络面。其中,刀具包络面Σg、加工目标齿面Σp和大轮包络面都在工件坐标系Opxpypzp中,它们沿指定的接触迹线相切,且有二阶切触。在小轮坐标系中,这三个曲面的位置关系如图9所示。在这三个曲面中,刀具包络面Σg可以由刀具曲面通过展成运动,由啮合方程求得;大轮包络面可以由大轮齿面通过指定的大小轮的相对运动,由啮合方程求得。

表3 刀具在展成曲面与目标齿面的最大偏差δmax

图8 包络逼近法展成的小轮凹面与理论齿面凹面的偏差分析拓扑图(μm)

图9 大轮齿面包络面、小轮加工目标齿面和刀具齿面包络面之间的关系
加工目标齿面Σp要依据加载齿面接触分析(load tooth contact analysis,LTCA)的计算结果确定。由于LTCA的计算很复杂,且所得到的结果一般还需试验验证其精度,因此,一般Σp确切的曲面方程很难得到。考虑到大轮包络面与Σp有图9所示的位置关系,且二者偏差很小,故在本文中提到的刀具包络面Σg逼近的目标曲面(Σp),在实际切齿计算中用大轮包络面替代。由图8和图9可知,当Σg逼近大轮包络面的最大偏差为δmax时,Σg逼近Σp的最大偏差δmaxb将不大于δmax,因此,这种替代对最终得到的齿面啮合特性造成的影响是可以控制的,即这种影响可以控制在LTCA结果所要求的范围内。上述分析表明:包络逼近法展成的小轮齿面始终能确保其与大轮齿面啮合时获得沿预定接触迹线上每一啮合点都具有预定的啮合特性。
在本例中,按上节所介绍的切齿方法得到的齿面与大轮包络面的偏差最大值为0.45μm,与目标齿面的偏差最大值会小于这个值。进一步研究表明,如果适当改变刀具的形状,还可以进一步降低偏差,理论上可以证明曲面的包络逼近方法可以充分(无限)逼近加工目标曲面。这个实例也表明本文所介绍的加工方法具有很高的精度。
5 结束语
提出了在Free-Form型五轴联动数控机床上加工具有预定啮合特性的点啮合齿面的新的加工方法——曲面的包络逼近法。在新的齿面展成方法中,刀具相对工件的展成运动是在内蕴齿面微分几何特性的曲面活动标架下设计的,这就确保了加工得到的齿面在指定的接触迹线附近与目标齿面有二阶切触,并能通过改变刀具在展成目标齿面上指定接触迹线各点时的姿态,使刀具的包络面的其他区域以最小偏差逼近目标齿面。实例计算证实了所提出理论和方法能确保所展成的点啮合齿面沿接触迹线的每一啮合点具有预定的啮合特性,并在接触迹线以外的齿面区域高精度地逼近加工目标齿面。
[1] 樊奇,让·德福.格里森专家制造系统GEMS开创弧齿锥齿轮及双曲面齿轮数字化制造新纪元[J].产品与技术,2005(4):87-93.
[2] Hermann J S.Gleason Bevel Gear Technology[M].Rochester,New York:The Gleason Works,1994.
[3] Litvin F L.Gear Geometry and Applied Theory[M].San Diego:PTR Prentice Hall,1994.
[4] 苏智剑,吴序堂.基于计算机数字控制弧齿锥齿轮加工机床的准双曲面齿轮的制造[J].机械工程学报,2007,43(5):57-63.
[5] Suh S H.Sculptured Surface Machining of Spiral Bevel Gears with CNC Milling[J].International Journal of Machine Tools & Manufacture,2001,41:833-850.
[6] Darboux G.Theory of Surfaces[M].New York:Chelsea Publishing Co.Inc.,1974.
[7] 陈维桓.微分几何[M].北京:北京大学出版社,2006.

