经验模式分解改进算法的比较

李宏伟，刘宇航，杨 辉

（1.阜新市水土保持工作总站，辽宁阜新123000；2.中水东北勘测设计研究有限责任公司科学研究院，吉林长春130061）

Hilbert-Huang变换(Hilbert-Huang transform,HHT)[1，2]是 Norden E.Huang1998年提出的一种数据处理方法,经验模式分解 (empirical mode decomposition,EMD)是该方法的第一步。HHT比传统方法更适合分析非线形、非平稳数据。现在在地震工程、结构损伤、系统识别、音频分析等领域都得到了广泛的应用。

1 EMD分解

EMD分解必须满足2个假设：（1)在整个数据长度中，极值点的数量(包括极大值点和极小值点)和过零点的数量必须相等或至多相差一个。（2)在任一时间点上，信号局部极大值确定的上包络线和局部极小值确定的下包络线的均值必须为零。

分解方法用局部极大值和极小值的包络来进行。所有的局部极大值用三次样条函数插值形成数据的上包络，所有的局部极小值通过插值形成数据的下包络，求出上包络和下包络的平均值，根据过零点和极值点数目、包络均值为零的条件，检查原始数据减去平均值得到的是否是一个固有模态函数(intrinsic mode function，IMF)，如果不是，就对得到的数据再次进行筛选，直至得到符合上述条件的IMF。原数据减去第一个固有模态函数当作新的数据再进行筛选，直至残余项成为一个单调函数，分解停止，最后得到一系列的固有模态函数和一个残余项。

随着HHT研究的深入和应用的拓展，还有一些关键的理论和实际问题需要完善和改进。EMD中有几个关键问题对分解效果有显著影响，分别是：IMF的筛分终止条件判断依据；边界的端点处理问题；各个IMF是否正交。

2 Rilling算法

有效的IMF必须满足在任一时间点上，信号局部极大值确定的上包络线和局部极小值确定的下包络线的均值为零，通常的做法是利用Huang提出的标准偏差法[1,2]。然而,这个判断条件的大小直接影响 IMF 的稳定性[3，4]。

2003年，Rilling等[5]对原始EMD分解中的滤波停止条件进行了改进，该方法的核心思想是在EMD 筛选中引入 3个参数 θ1，θ2，α 作为判断依据[6]。具体过程是：确定时程曲线x(t)的所有极值点，所有的局部极大值用三次样条插值函数形成数据的上包络线fmax(t)；所有的局部极小值通过插值形成数据的下包络线fmin(t)，上包络和下包络的平均值仍记作m(t)。

计算模态幅值：

并引进新的评估函数：

筛选停止条件有2个：

（1）σ(t)≤θ1的时间(在等步长离散情况下为步长数)与全部持续时间之比至少达到满足1-α成立(其中α常取为0.05)，其目的是为了保证大多数数据波动的平均值足够小。

（2）σ(t)≤θ2，其目的是为了限制 EMD 分解时局部数据最大漂移。

与Huang的方法相比，σ(t)更能反映IMF的均值特性，且两个相互补充，使信号只能在某些局部出现较大波动，从而保证整体均值为零[7]。

为考查上述方法的效果，采用一个简单的解析信号：

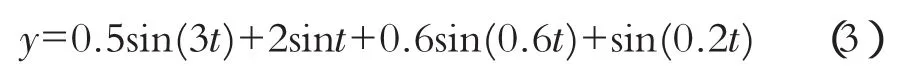
分别用标准偏差法和Rilling滤波方法进行计算比较。取 θ1＝0.05，θ2＝10θ1，α＝0.05，时间取 50s。

从平均频率和平均振幅两个方面衡量两种方法的优劣。Rilling算法得到的IMF和标准偏差法得到的IMF频率与原始波频率并没有明显的差异，但是从振幅来看，Rilling算法的振幅和原始波更为接近，特别在c3频段，两者的差别较大，所以Rilling的控制方法是优于标准偏差法的。

3 多项式拟合求端点的极值

EMD分解中，通过对原数据中的上极值点和下极值点分别进行三次样条插值拟合再求平均得到包络均值，在样条插值时常常不能确定端点处的极值，就会在样条插值时产生数据的拟合误差。不断累积的误差就会由端点处向内逐渐传播，信号的两端会出现严重的扭曲。

3.1 多项式拟合算法

端点常常并不是极值，如果能够根据极值点序列中端点以内数据的规律得出该序列在端点处的近似取值,则可以防止对端点插值出现较大的摆动。

取出原极值点序列最左端的3个极值点(如果极值点序列的个数小于3个则取序列中所有元素),对所取的极值点求出拟合多项式,计算出多项式对应数据序列左端点处的函数值,并把此函数值作为极值点序列在该端点处的近似取值,同理求出极值点序列在右端点处的近似取值。最后利用3次样条函数对新极值点序列进行插值得到上下包络线。3次样条函数在端点处有值可依,避免了上下包络线的摆动。

具体步骤如下：

（1）根据具体问题，确定拟合多项式的次数n；

（2）计算 Sr和 tq

式中m为终点的下标；xi是离散数据点的横坐标；r=0，1，2，…，n，n＜m。

其中 yi为离散数据点的纵坐标，q=0，1，…，n。

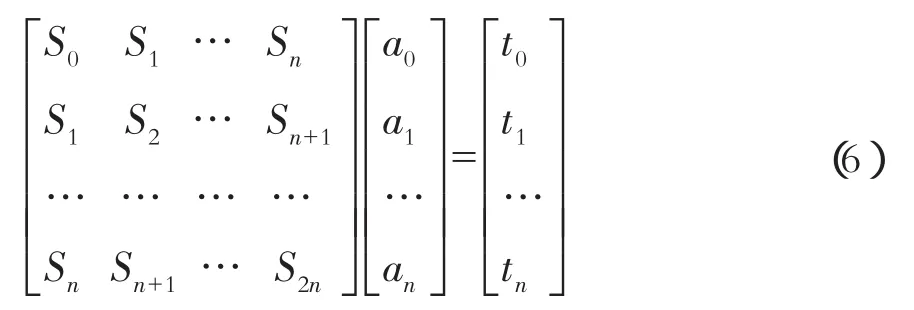
（3）由方程组(6)得到 a0，a1，…，an最后写出拟合多项式[8]：

3.2 运用多项式拟合算法对数据进行处理

将式（3）的解析信号通过多项式拟合算法分解，可以看到在c3和c5分量（图略）的端点处，发生了较大的区别，这是因为原来采用的端点处理手段是忽略内部数据信息的方法，只是强制解决了端点飞翼，但同时也引入了较大的端点误差，所以在端点处出现了较大偏差。进一步对照原始信号图（图略）中的对应c3频段波形可以证明，经过多项式拟合算法得到的结果，更加符合实际。

4 正交化经验模态分解方法

Huang提出的EMD分解方法不能从理论上保证严格的正交性，仅仅能从数值上表明各IMF是近似正交的，不正交意味着解不唯一，也意味着信号冗余度的增加和不能严格遵守能量的守恒定律。

4.1 固有模态函数的正交性判断依据

Huang定义了整体的正交性指标和两个分量

之间的正交性指标，离散数据的整体正交性指标[8]：

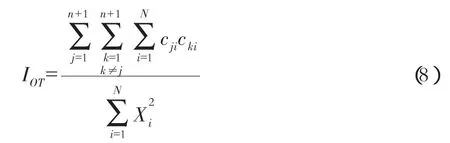
分量的正交性指标：

此外还可以通过一个能量指标来进一步表明各分量之间的正交性[9]，设原始信号的能量为Ex：

各分量的能量为

如果分解出来的各个IMF分量是正交的，那么信号分解后的总能量应保持不变且各分量之间的泄漏能量为零，即：

当各IMF分量之间完全正交时，IOT和IOjk的值应等于零。

4.2 IMF的正交化处理

对已经得到的各阶IMF分量进行正交化,可以得到完全正交的各阶IMF分量，步骤如下：

（2）正交化的IMF分量记做ci(t)，对第一个IMF分量，暂不作处理，即令c1(t)=c1(t)。

（3）从原来EMD分解得到的第二个IMF分量开始进行正交化处理：

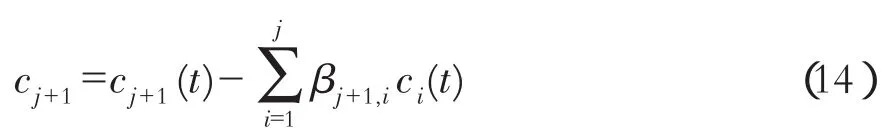
这样就可以从第j+1阶开始，消除各IMF中含有的非正交成分，可以得到信号X(t)的第j+1阶真正的正交化 IMF分量 cj+1(t)(j=1，2，…，n)。

（4）对 cj(t)做线性变换：

其中

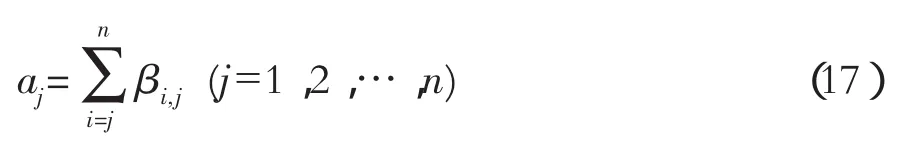
当 i=j时，βi,j=1。

通过这样的线性变换得到的各阶c*j(t)是完全正交的，而且是完备的。

4.3 应用正交化EMD方法对数据进行处理

对式(3)中的信号使用正交化EMD方法进行分解。把各IMF分量之间的正交性指标列于表中（表略），由于正交性是具有对称性的，表中数字是采用原始EMD分解得到的各IMF分量之间的正交性指标,表中下三角的数字是用新的方法分解的IMF分量之间的正交性指标。

按照原始EMD分解得到的整体正交化指标是0.064122，按正交化处理得到的整体正交化指标是0.0006443，相差近100倍，可以看出原始EMD分解得到的各IMF之间正交化程度是比较差的。基于正交化分解得到的各阶IMF分量之间的正交化程度要远好于原始EMD分解，其正交性指标都在10-16以下。从能量分析，真实信号的总能量是Ex＝3392.2，原始EMD分解的误差为8.89%,新的正交化EMD分解的误差仅为2.48%(见表1)。

可以发现，新的正交化EMD分解的缺点是：使每个IMF产生毛刺，而毛刺是由于扣除非正交分量的高频信号产生的结果，因为每个后面的IMF都要减去和前面IMF正交的部分，这就使得本来比较光滑的IMF变得不那么光滑。

5 结语

（1）Rilling算法可以控制信号在全局都不能出现超过标准的波动(σ（t）≤θz)，而即使在某些局部出现较大的波动，这些大的波动也只能是全部时间的一小部分，优于标准偏差法的全局笼统控制。

（2）端点处理采用多项式拟合方法，能够根据数据内部变化的走势来判断数据端点应该采用的包络线位置，可以避免延拓方法带来的主观因素和误差。

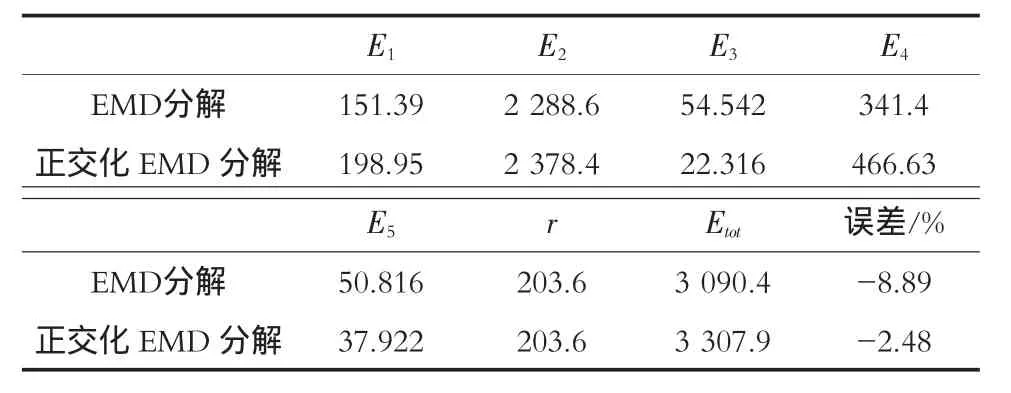
表1 信号总能量、各分量能量及各分量能量之和

（3）正交化处理能够保证各个IMF是严格正交的，使得各个IMF分量的能量和与原始波形的能量误差很小，符合工程需要。

[1]Norden E.Huang,Zheng Shen,Steven R.Long,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proc.R.Soc.Lond.A,1998,454:903:995.

[2]HUANGNE，SHENZ，LONGSR.Anewviewofnonlinear waterwaves:the Hilbert spectrum[J].Ann Rev Fluid Mech,1999,31:417-457.

[3]沈国际,陶利民,陈仲生.多频信号经验模态分解的理论研究及应用[J].振动工程学报,2005,18(1):91-94.

[4]丁康.平稳和非平稳振动信号的若干处理方法及发展[J].振动工程学报,2003,16(1):1-10.

[5]RILLING G,FLANDRIN P,GONCALVES P.On Empirical ModeDecompositionanditsalgorithms[C].IEEEEURASIP Workshop on Nonlinear Signal and Image Processing,Grado(I),June9-11,2003.

[6]李彬彬,袁中凡,杨春生.改进HHT算法及在心音信号分析中的应用[J].四川大学学报,2007,39(4):160-163.

[7]郑天翔,杨力华.经验模态分解算法的探讨和改进[J].中山大学学报,2007,46(1):1-6.

[8]刘慧婷,倪志伟,李建洋.经验模态分解方法及其实现[J].计算机工程与应用2006(32):44-47.

[9]楼梦麟,黄天立.正交化经验模式分解方法[J].同济大学学报,2007,35(3):293-298.

[10]Qiuhui Chen,N.E.Huang,et al.,A B-spline approach for empiricalmodedecompositions,AdvancesinConmutational Mathematics,2006,24:171-195.

[11]ZHAO Jin-ping,HUANG Da-ji.Mirror extending and circularspline function for empirical mode decomposition method[J].Journalof Zhejiang University(Science),2001,2(3):247-252.