基于时变自回归参数模型的滚动轴承智能故障诊断

李健宝 彭 涛

1.湖南工业大学，株洲，412008 2.中南大学，长沙，410083

0 引言

滚动轴承是旋转机械中应用最广泛的零部件之一，轴承工作状况的好坏决定着机器能否正常工作。统计显示，旋转机械设备的功能失效有30%是由轴承故障引起的，因此，对滚动轴承进行故障诊断具有十分重要的意义。

轴承运行时的振动信号是典型的非线性非平稳时间序列，很难用一个完全确定的数学函数来表达。因而对轴承进行故障诊断常通过提取振动信号的特征参数并建立其与运行状态之间的关系来实现。时间序列分析（time series analysis）通过将观测数据拟合为一个参数模型，实现对系统动态特征与内在结构关系的近似描述［1］。常用的时间序列参数模型，如自回归（autoregressive，AR）模型、滑动平均（moving average，MA）模型和自回归滑动平均（autoregressive moving average，ARMA）模型等，都是在假定数据序列为平稳的条件下建立的，在实际应用中存在一定的局限性。时变参数模型因其具有较高的非平稳信号时频分布分辨率而受到普遍关注［2－6］。时变自回归 （time－varying autoregressive，TVAR）模型是目前应用最多的一种时变参数模型，如文献［5］通过对滚动轴承振动信号的TVAR模型求取的时频谱进行奇异值分解，提取奇异值作为特征参数，文献［6］对转子系统振动信号的TVAR模型，提取其基函数的组合权值作为特征参数，实现了对旋转机械的状态监测和故障诊断。目前，直接提取振动信号TVAR模型的时变参数作为反映机械设备运行状态特征参数的研究还不多见。

通过对轴承振动信号的TVAR模型的时变参数进行大量实验研究分析，发现时变参数能有效利用信号的时频分布信息，较好地表征非平稳信号的动态特征。为此，本文提出一种基于时变自回归参数模型的滚动轴承智能故障诊断方法。首先对滚动轴承的振动信号建立时变自回归参数模型，提取时变参数的均值作为反映轴承运行状态的特征参数，然后采用支持向量机（support vector machines，SVM）分类器实现对滚动轴承的智能故障诊断。

1 TVAR建模原理

对离散时间序列｛x（t），t＝1，2，…，N｝可建立如下TVAR模型：

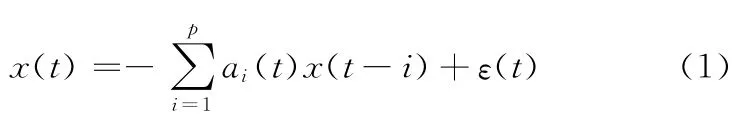
式中，ai（t）为时变参数；p 为模型的阶次；ε（t）为均值为零、方差为σ2的白噪声。

时变参数ai（t）可用一组基函数的线性组合来表示［7］，即

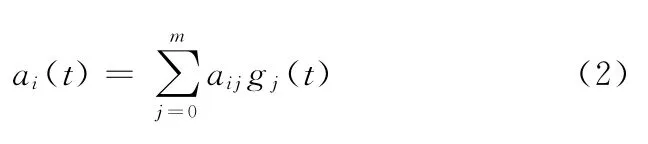
式中，m为基函数维数；aij为基函数的组合权值；gj（t）为一组基函数。

常用的基函数有时间多项式基函数、傅里叶基函数、离散余弦基函数、勒让德多项式基函数和离散长球序列基函数等。由于轴承的振动信号可近似看作是循环周期信号［8-9］，而傅里叶基函数比较适于周期变化情况［10］，因此，本文采用傅里叶基函数，其表达形式为

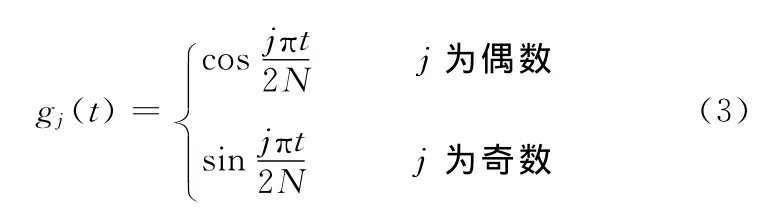
将式（2）代入式（1）可得

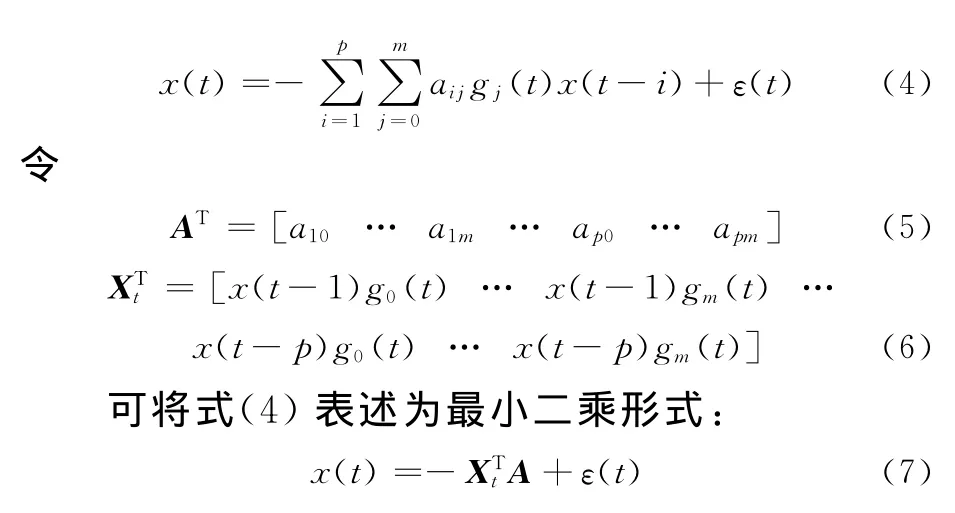
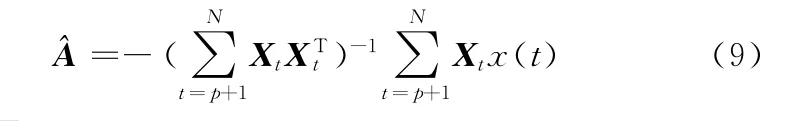
进而可以求得模型残差ε（t）的方差σ2的最小二乘估计值：

利用式（9）求解模型参数时存在矩阵求逆的问题，当矩阵较大时，求解式（9）需要很大的存储空间和很长的时间。可以利用递推算法来求解式（9）。令则有如下递推算法［11］：

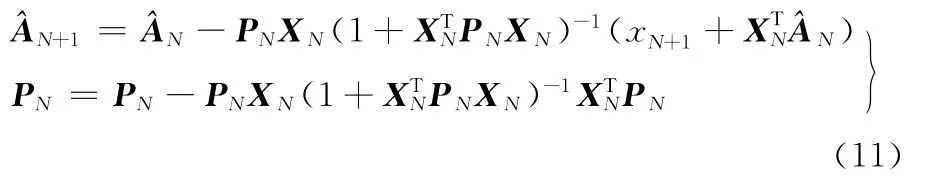
估计出参数a10，…，a1m，…，ap0，…，apm后，就可根据式（2）求出模型参数ai（t）在各个时刻的值。

在实际应用中，模型的阶次通常是未知的，需要根据观测数据来适当地判定。AIC准则（akaike information criterion）是目前应用比较广泛的定阶方法，通过使平均对数似然函数为最大或Kullback信息量最小来确定AR模型的最佳阶次，其定义如下［12］：

2 基于TVAR模型的智能故障诊断方法

本文提出的滚动轴承智能故障诊断方法流程见图1，首先对滚动轴承运行时的振动信号建立时变自回归参数模型，用模型参数的均值构建特征向量来表示第i个样本信号（i＝1，2，…，N），然后采用支持向量机实现状态的智能识别。

图1 故障诊断流程图

具体实现过程如下：

（1）分别在轴承正常、内环故障、滚动体故障和外环故障状态下，按一定的采样频率进行采样，获得一定数量的振动信号作为样本（1024个采样点为一个样本）。

（2）对来自传感器的含有大量噪声的原始信号进行低通滤波等预处理，得到待分析信号x（t），利用式（12）确定p、m，然后由式（11）估计出参数A，建立时变自回归参数模型。

（4）利用训练样本对SVM分类器进行训练，SVM的建立详见文献［13］。

（5）用训练好的SVM多类分类器对测试样本进行故障模式识别。

3 实验分析

3.1 实验 Ⅰ

本部分采用的数据全部来自美国Case Western Reserve大学滚动轴承数据中心［14］。测试平台如图2所示，由1492W（2马力）三相交流电机（左）、转矩传感器（中）、测力计（右）和电子控制装置（未显示）组成。电机轴由测试轴承支撑，通过放电加工（electro－discharge machining，EDM）技术在测试轴承中植入单一局部故障缺陷，故障点直径分别为177.8μm（7mil）、355.6μm（14mil）和533.4μm（21mil），深度为279.4μm，测试轴承为6025－2RS JEM SKF型深沟轴承。

图2 测试台

振动信号通过加速度传感器采集，采样频率为48kHz。在不同电机负载／转速工况工作条件（0、746W、1492W 和2238W）、4种不同故障类型（正常状态、滚动体故障、内环故障、外环故障）和3种不同故障程度情况下记录振动加速度信号数据，共获得40组数据（正常状态无故障大小，只需采集不同工况下的4组数据），并将每组数据以1024个采样点为一个样本构成一组样本集。按相同负载／转速、相同故障程度分类，可将40组样本集分成12个数据集，每个数据集由在相同负载／转速和相同故障点直径条件下的4种不同故障类型样本集组成，如表1所示，表中，N表示正常状态，I表示内环故障，B表示滚动体故障，O表示外环故障（下同）。以相同负载／转速、相同故障类型分类（不包含正常情况），亦可将36组样本集分成12个数据集，每个数据集由在相同负载／转速和相同故障类型条件下的3种不同故障点直径的样本集组成，如表2所示，表中，FD7表示故障直径为177.8μm，FD14 表示故障直径为355.6μm，FD21表示故障直径为533.4μm（下同）。按第2节所述方法对各数据集进行仿真实验研究，在此以数据集D007＿0为例，对具体过程加以详细说明。

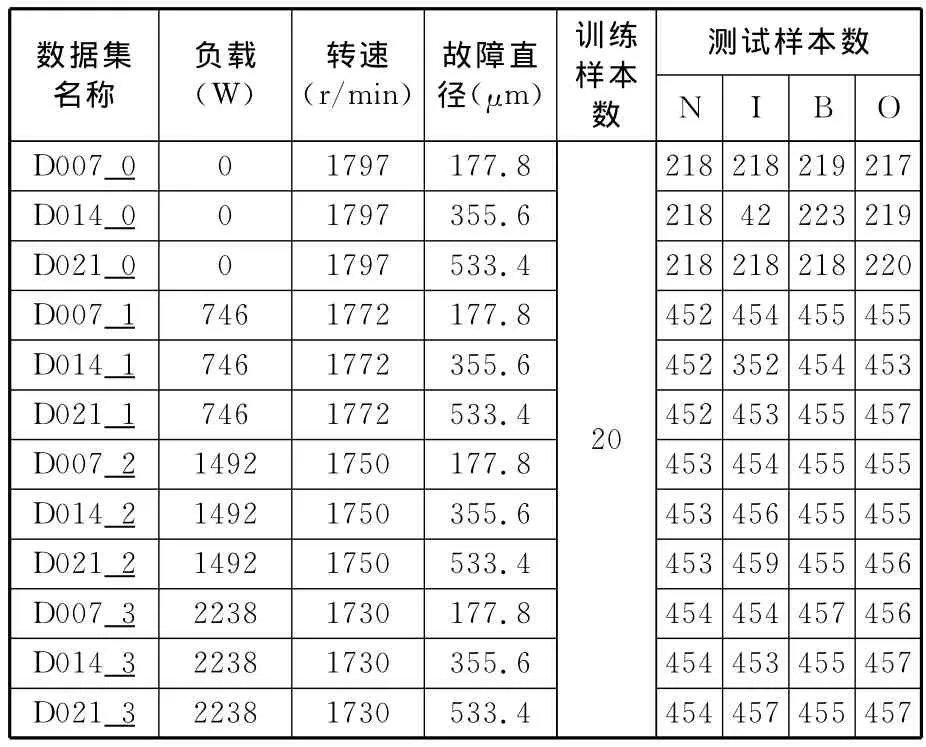
表1 样本集分类描述（一）

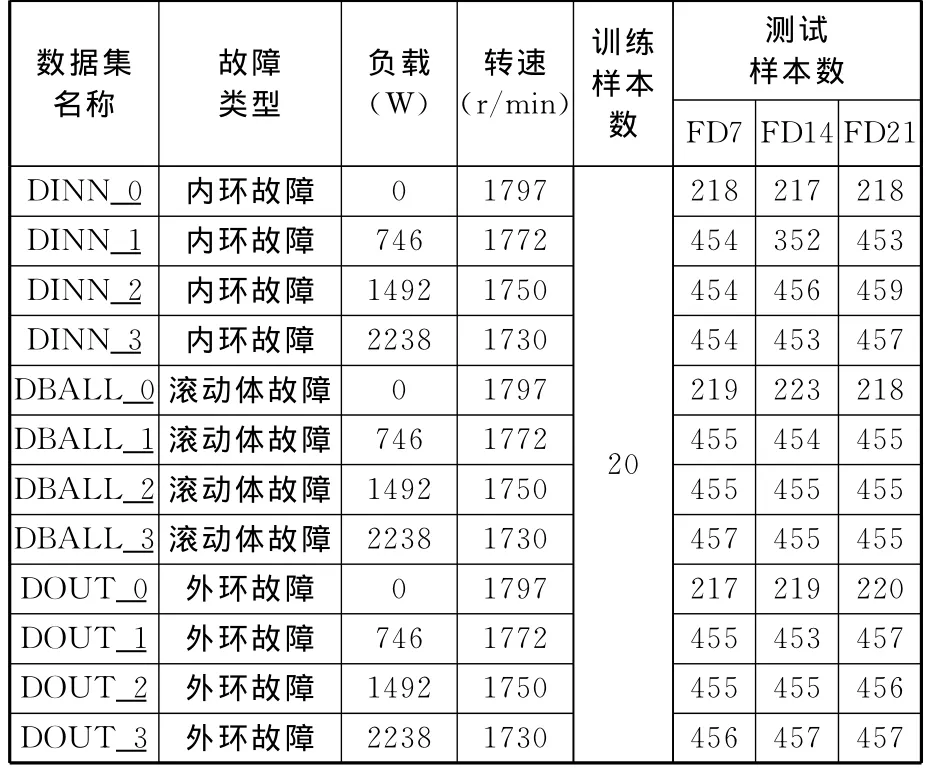
表2 样本集分类描述（二）

选取4种故障类型的样本各一个，进行模型阶次（p×m）的确定。得到正常状态的最佳模型阶次为19×4，内环故障的最佳模型阶次为18×3，滚动体故障的最佳模型阶次为18×3，外环故障的最佳模型阶次为20×3。为便于进行SVM分类，需对数据集中的各样本建立相同阶次的TVAR模型，为此，选取最佳模型阶次为18×3。然后求出数据集中各样本的时变参数，图3所示为数据集D007＿0中每类故障各一个样本的部分时变参数情况。可见，不同故障类型的时变参数之间具有较大的区分度，如正常和内环故障的时变参数a1（t）与滚动体和外环故障的时变参数a1（t）之间有较大的差异等。因此，时变自回归模型的参数可以用作反映轴承运行状态的特征参数。

如果直接将时变参数作为表征轴承运行状态的特征向量输入到SVM，则一个样本的输入即为18×1024＝18 432维的高维向量，不利于SVM的处理，且影响分类效率。为此，在求出轴承振动信号的TVAR模型参数的基础上，需进一步研究时变参数的特性来获取低维特征参数，用以表征轴承的运行状态。本文在建立轴承振动信号的TVAR模型后，分别对每一个时变参数求平均，这样18个时变参数可获得18个平均值，则特征参数的维数降至18维。在大量实验研究分析的基础上发现，在轴承的不同运行状态下，对应的TVAR模型参数的均值亦有着较大的可分性。以数据集D007＿0为例，各样本的部分TVAR模型参数的均值如图4所示，显然，不同故障类型所对应TVAR模型参数的均值之间仍具有较大的区分度。选取表2中的数据集DINN＿2进行分析，结果如图5所示，可见，不同故障程度所对应TVAR模型参数的均值之间同样具有较大的区分度。大量实验研究分析表明，时变自回归模型参数的均值可以较好地刻画运行在不同负载条件下不同故障类型、不同故障程度轴承的动态特性，因而可以用作描述轴承振动信号的特征参数。

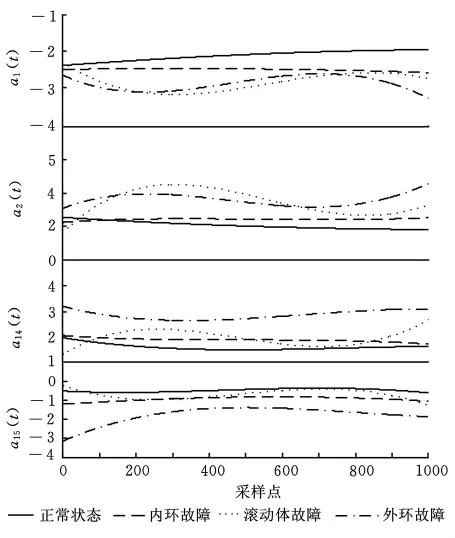
图3 单个样本的部分时变参数

图4 D007＿0各样本的部分时变参数均值

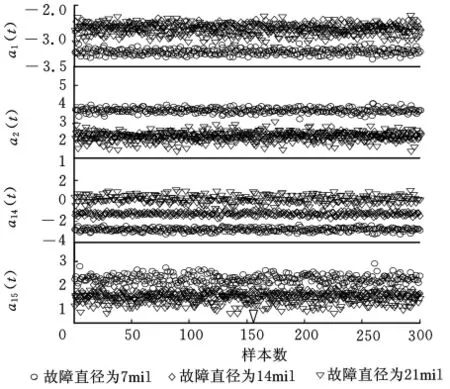
图5 DINN＿2各样本的部分时变参数的均值

因此，对轴承的振动信号建立18×3阶TVAR模型，采用模型参数的均值作为反应轴承运行状态的特征参数，即构建特征向量用以反映轴承的运行状态。由特征向量Xi构造出训练样本集和测试样本集利用训练样本对SVM分类器进行训练，并用训练好的SVM多类分类器对测试样本进行故障模式识别。

对表1、表2中的数据集分别进行仿真实验，结果如表3和表4所示，各状态均有较高的分类识别率。仿真实验结果说明，采用本文所提的特征提取方法可以有效地提取出反映轴承运行状态的特征参数，从而实现滚动轴承故障的有效诊断。将本文方法与文献［6］所提方法进行对比实验（均采用SVM作为分类器），限于篇幅，此处只列出各数据集整体分类识别率，分别如表3和表4中文献［6］方法一栏所示，可知，采用本文方法所获得的整体分类识别率均高于文献［6］所述方法，结果进一步说明了本文所提方法的有效性。

表3 测试结果（一）

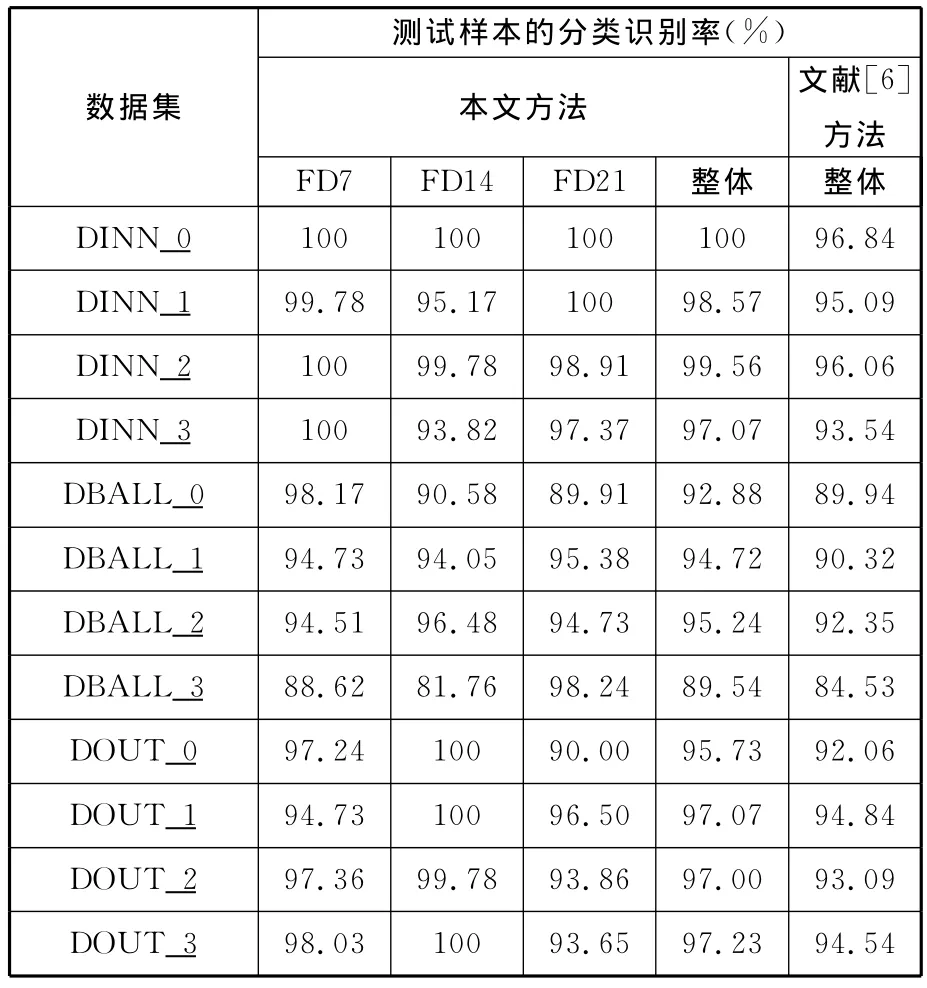
表4 测试结果（二）

3.2 实验Ⅱ

本实验是在笔者所在实验室的QPZZ－Ⅱ型旋转机械故障平台上进行的，装置如图6所示，轴承型号为N205型滚珠轴承。分别在不同负载、转速下通过安装在轴承座外壳上的加速度传感器采集轴承运行时的振动信号，采样频率为20kHz，模拟的故障分别为外环、内环、滚动体出现细小裂纹的情况。然后采用第2节所述的方法对其进行故障诊断，同样以1024个采样点为一个样本，得到各状态的训练样本和待识别（测试）样本数分别为20和480，诊断结果如表5所示。由表5可知，在不同的故障发生形式下，采用本文所提的方法对各种故障类型进行分析亦具有较高的分类识别率，说明本文所提方法具有一定的实用性。

图6 QPZZ－Ⅱ旋转机械故障模拟平台

表5 验证实验结果

4 结束语

通过对滚动轴承的振动信号建立时变自回归参数模型，提出了一种用模型的时变参数均值构建表征轴承运行状态特征参数的方法，经支持向量机分类器对所提取特征进行故障诊断与分类，实现了滚动轴承故障的智能诊断。利用不同运行状态下的数据进行仿真实验，结果证明了本文所提方法的有效性。

［1］ 吴今培，孙德山.现代数据分析［M］.北京：机械工业出版社，2006.

［2］ Chen Z S，Yang Y M，Hu Z，et al.Detecting and Predicting Early Faults of Complex Rotating Machinery Based on Cyclostationary Time Series Model［J］.Journal of Vibration and Acoustics，2006，128（5）：666－671.

［3］ Zhan Y M，Mechefske C K.Robust Detection of Gearbox Deteriorateion Using Compromised Autoregressive Modeling and Kolmogorov－Smirnov Test Statistic－PartⅠ：Compromised Autoregressive Modeling with the Aid of Hypothesis Tests and Simulation Analysis［J］.Mechanical System and Signal Processing，2007，21：1953－1982.

［4］ 王胜春，韩捷，李志农，等.基于TVAR的自适应时频分析及在故障诊断中的应用［J］.轴承，2007（6）：28－31.

［5］ Wang G F，Luo Z G，Qin X D，et al.Fault Identification and Classification of Rolling Element Bearing Based on Time－varying Autoregressive Spectrum［J］.Mechanical System and Signal Processing，2008，22：934－947.

［6］ 张龙，熊国良，柳和生，等.基于时变自回归模型与支持向量机的旋转机械故障诊断方法［J］.中国电机工程学报，2007，27（9）：99－103.

［7］ Pally R K，Louis Beex A A.Modeling of Time－varying Instantaneous Frequency in a Finitely Correlated Environment［C］／／In 16th International Conference on Digital Signal Processing.Santorini，2009：1165－1170.

［8］ McCormick A C，Nandi A K.Cyclostationarity in Rotating Machine Vibrations［J］.Mechanical System and Signal Processing.1998，12：225－242.

［9］ Capdessus C，Sidahmed M，Lacoume J L.Cyclostationarity Processes：Application in Gear Faults Early Diagnosis［J］.Mechanical System and Signal Processing，2000，14：371－385.

［10］ 张海勇，李勘.非平稳随机信号的参数模型分析方法［J］.系统工程与电子技术，2003，25（3）：386－390.

［11］ Girault J M，Ossant F.Time－varying Autoregressive Spectral Estimation for Ultrasound Attenuation in Tissue Characterization［J］.IEEE Transactions on Ultrasonics，Ferroelectrics，and Frequency Control，1998，45（3）：650－659.

［12］ Zhan Y M，Jardine A K S.Adaptive Autoregressive Modeling of Non－stationary Vibration Signals Under Distinct Gear States.Part 1：Modeling［J］.Journal of Sound and Vibration，2005，286：429－450.

［13］ 杨正友，彭涛.基于振动信号分析和支持向量机的滚动轴承故障诊断［J］.湖南工业大学学报，2009，23（1）：96－99.

［14］ Case Western Reserve University.Bearing Data Center［EB／OL］.［2010－02－10］.http：／／www.eecs.cwru.edu／laboratory／bearing／welcome＿overview.htm.