速度前瞻控制中的伺服动力学约束条件

杨征宇 李 宁 闫 华

南京工程学院，南京，211167

0 引言

在数控加工中，复杂的加工路径被CAM的后置处理器分解成一系列的微小路径段。数控系统对每一小路径段进行插补运算和加减速控制。对于由大量的微小线段组成的加工路径，如果还按照处理长线段的方式，在每个线段内独立地进行加减速控制，将会导致伺服系统频繁启停，加工缓慢［1］。解决这一问题的办法是采用速度前瞻技术，将相邻的小线段当成一个整体，提前考虑前面的若干个小路径段的情况，以决定当前插补线段的速度。

目前，国内外对小线段高速加工问题的研究已经取得了一定的成果，文献［1］研究了基于前瞻技术的微小线段连续轨迹插补方法，通过预测轨迹的曲率变化，自适应调整进给率以达到高速高精加工的目的。文献［2－3］研究了基于样条技术的前瞻插补方法，得到了样条曲线和直线的衔接点处位置、斜率、曲率连续性的条件，并利用曲率门限标准识别拟合曲线的锐角，计算拟合曲线内相邻线段衔接处与锐角处的进给率，另外也研究了NURBS样条曲线的实时自适应前瞻插补算法。文献［4］基于机床伺服驱动的功率限制，提出了速度约束条件。但是在机床进给控制中，伺服驱动电机总是工作在恒转矩状态，而非恒功率状态，因而所提出的速度约束条件有一定的局限性。文献［5］构建了插补几何元素衔接矢量角模型，并把S形加减速算法运用到速度前瞻算法，使得整个插补过程更加柔顺。文献［6］研究了小线段高速加工速度衔接数学模型，提出了在相邻路径段转角处的加工速度约束条件。但是这些约束条件是根据运动学原理提出的，没有考虑机床的动力学伺服特性对小线段加工速度衔接规律的影响。文献［7］讨论了微小线段之间过渡的问题，提出了当剩余距离小于一个插补周期里的运行距离时，提前变换方向，采用斜线连接过渡的方法，但是没有讨论速度的约束条件及变化规律。

本文从机床伺服驱动系统的动力学特性出发，研究了在高速加工中相邻小线段间拐角处的速度衔接数学模型，分析了机床伺服系统的动力学特性对速度衔接过渡过程的影响，给出了相应的速度约束条件。

1 小线段加工速度衔接过程分析

本文以空间直小线段为例，分析速度衔接过渡过程。如图1所示，加工路径是从小线段An－1An，过渡到小线段 AnAn＋1。设在线段 An－1An上的终点加工速度是v1e，在线段AnAn＋1上的起点加工速度是v2s，为保证加工速度的平稳，应当有的夹角是θ，小线段An－1An与小线段AnAn＋1的夹角是π－θ。速度从v1e过渡到v2s是在一个插补周期Δ内完成的，设机床进给加速度为a，则有：

式中，（v1x，v1y，v1z），（v2x，v2y，v2z），（ax，ay，az）分别为v1e、v2s、a在三个坐标轴上的投影。

图1 小线段衔接

根据图1，在由v1e和v2s组成的三角形中，有

将式（2）直接代入式（3）并整理可得

在式（4）等号右边的是一个小于零的量，等号左边的则是三个坐标轴方向的速度和加速度的乘积之和。由式（4）可以看出，在三个坐标方向的速度和加速度的乘积中，至少有一个是负的，并且这个负的乘积项在数值上居主导地位。这就说明，在小线段速度衔接的过程中，无论线段的方向角怎么变化，至少有一个坐标轴方向处于制动减速状态，并且这个坐标轴方向的伺服驱动机构的制动减速性能决定了小线段加工速度衔接的质量。

2 小线段衔接速度的约束条件

在机床进给驱动中，伺服驱动电机工作在恒转矩控制状态下，短时间里允许输出转矩超过额定值，但是输出功率以额定值为上限。对于处于制动状态下的坐标轴来说，伺服电机短时工作在发电状态，其提供的制动转矩使机床减速。位置进给伺服系统加减速性能源于静态和动态两个方面：在静态方面源于伺服电机最大输出转矩的限制；在动态方面源于伺服系统内部的速度环带宽对速度过渡快速性的限制。下面分别对这两方面进行讨论。

2.1 伺服电机的最大输出转矩限制与小线段衔接速度的关系

如图1所示，设小线段An－1An的方向角是（αn，βn，γn），小线段AnAn＋1的方向角是（αn＋1，βn＋1，γn＋1）。从线段An－1An到线段AnAn＋1，加工进给速度的方向发生改变，但大小不变，均为vn。对各个坐标轴，伺服系统的运动速度发生了改变，其加速度为

各个坐标轴的最大加速度受限于伺服电机最大输出转矩。为不失一般性，可以假定各轴均采用直接驱动的方式，并假定各丝杠螺距相同，则各个轴的最大加速度为

式中，Txmax、Tymax、Tzmax为三个轴伺服电机的最大驱动力矩；amx、amy、amz为根据电机最大力矩确定的各轴的运动加速度；Txf、Tyf、Tzf分别为三个轴方向的切削反抗力矩；Jx、Jy、Jz为折合到伺服电机轴上的有效转动惯量；L为传动丝杠的螺距；m为垂直运动的有效质量。

如果主要研究制动减速的坐标轴，那么在制动减速的过程中，切削反抗力矩与电机的制动力矩是同向的，并且大大小于电机的制动力矩。因此可以令

小线段过渡时的速度vn应当满足：

2.2 速度环带宽与小线段衔接速度的关系

一般数控机床的位置进给伺服系统采用半闭环的控制方式，位置控制器采用“比例＋前馈”的控制策略，内部的速度环可以用一个二阶环节来表述［8］，如图2所示。在图2中，Kp是位置比例增益，F是前馈增益，Kz是机械传动机构的增益，Kv是速度的闭环增益，ωN是速度环带宽，ζ是速度环的阻尼系数。

如上所述，在小线段衔接的过程中，沿加工路径的进给速度大小不变，方向改变，因而至少有一个坐标轴上的伺服系统的指令速度会发生较大改变，并且这一改变是发生在一个插补周期Δ内的。事实上，各个坐标轴上伺服的最大加速度，不仅受限于伺服电机的输出转矩，还必须受限于速度环的带宽。

图2 伺服系统动态结构图

在机床加工过程中，为了保证加工质量，伺服系统必须单调跟随控制指令，不应出现超调和振荡现象。理论和实践均表明，速度环频带宽度越宽，越能够保证伺服系统良好的跟随性能。若带宽固定，减小指令加速度，也可使伺服系统跟随性能变好。

伺服系统的速度环带宽是一个重要的设计指标，目前对一般的国产伺服驱动器而言，这一指标达到了250Hz左右，国际上较先进的伺服驱动器的速度环带宽可达400Hz。指标是在伺服电机惯量与负载惯量相匹配的情况下达到的。速度控制环节的阻尼系数ζ也是一个重要的性能指标，与传动机构的惯量和刚度以及黏性摩擦因数等有关［8］。在实际应用中，速度环一般是“微欠阻尼”的，可以用速度超调量σ来衡量速度跟随响应的品质。利用MATLAB7.0的数值计算和图形功能，可以得出σ与速度环带宽、运动加速度、阻尼系数ζ等的关系。

在速度环带宽的范围为100～500Hz、运动加速度的范围为0.1～1.0m／s2条件下，分别计算了在4种阻尼情况下，速度超调与带宽及加速度的关系，计算结果如图3所示。在计算中，利用了自制的伺服性能测试台的一些机械参数：转动惯量0.0026kg·m2，丝杠螺距8mm。

图3显示的结果表明，速度超调与运动加速度、带宽、阻尼等都有关系，以阻尼系数ζ＝0.800的情况为例，若希望将速度超调控制在0.5%以下，如果速度环带宽为400Hz，则坐标轴运动加速度不大于0.5m／s2即可；如果速度环带宽为250Hz，则坐标轴运动加速度则不能大于0.3m／s2。

若三个坐标轴根据带宽、阻尼等条件而确定的运动加速度分别是ahx、ahy、ahz，并且令

那么小线段过渡时的速度vn还应当满足：

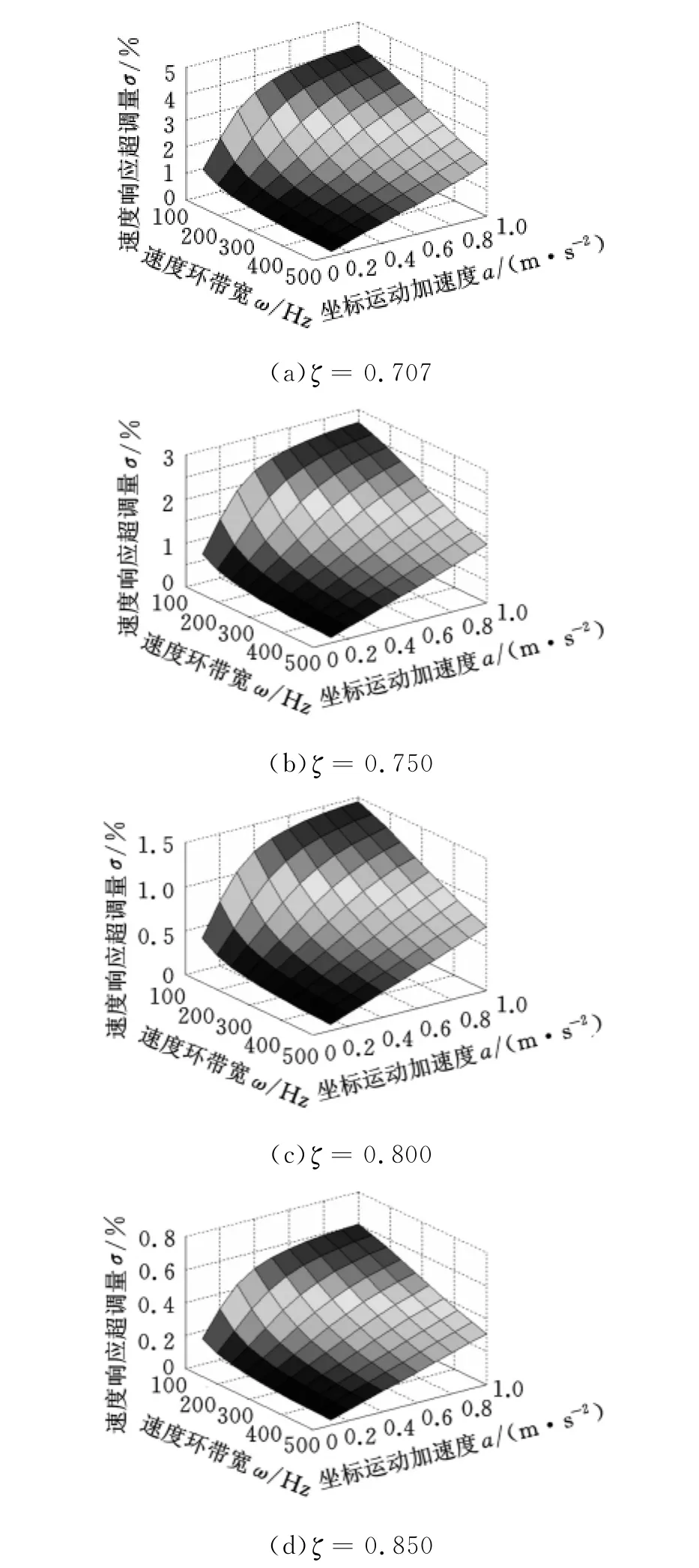
图3 速度超调与带宽和加速度的关系

3 约束条件在速度前瞻算法中的应用

前面分析了伺服系统的动力学特性对数控机床连续小线段衔接速度的约束条件，这样的约束条件可以应用在速度前瞻算法中。具体方法如下：

式中，vns为小线段的起点速度；vne为终点速度；s为小线段的长度；anx、any、anz为三个坐标轴方向的实际加速度；ahx、ahy、ahz分别为按照速度环带宽确定的三个坐标轴方向的最大加速度。

4 实例验证

将速度前瞻技术应用到数控加工中还涉及诸如工艺参数、刀具系统、数控编程等方面的技术问题，本文试图从分析机床伺服动力学特性的角度，对线段间的衔接速度作一些估计和限制，希望藉此提高加工效率并保证速度衔接的平滑性。

本文选用了如图4所示的某乘用车发动机盖冲压模具型面的数控铣削加工作为前三节理论研究的验证实例。数控加工设备为意大利萨克曼兰鲍蒂公司的龙门式五轴数控高速铣削中心SPEDH60。该加工中心采用连续叉式铣头，工作台三个轴的行程分别为6000mm、3500mm、1500mm，快速进给速度达20m／min，主轴转速为18 000r／min，数 控 系 统 为 Simens840D，支 持NURBS插补格式。发动机盖零件冲压凹模型面的数控铣削从粗加工到局部精整加工共有8道工序，本文选取XY平面中曲率变化大的6个圆角处的加工路径进行比较研究。选用第8道精整工序，在应用CAM对加工区域进行后置处理时加入速度前瞻约束条件，生成相应的刀具轨迹，如图5所示。在凹模模型上进行精整铣削加工的比对切削实验，常规数控程序切削时间为56min33s，引入速度前瞻约束条件程序的切削时间为44min15s，提高加工效率约20%，切削表面质量达到零件设计要求。图6所示为凹模型面精加工刀具轨迹。

图4 发动机盖外板零件数模

图5 考虑速度前瞻数控加工的刀具轨迹设计

图6 凹模型面精加工刀具轨迹

5 结束语

本文分析了数控机床伺服系统的动力学性能对空间小线段连续加工衔接过程的影响。从各个坐标轴电机的最大力矩以及速度环带宽等伺服性能参数出发，得到了对衔接过程的速度和加速度影响的一些约束条件，这些约束条件主要与相邻线段的方向角的变化有关，在三个坐标方向上，方向角变化最大的方向一般是受约束最严格的。在数控实际加工中的验证表明，将本文给出的约束条件应用到速度前瞻算法中，可以在保证速度衔接的平滑性的前提下，有效地缩短加工时间，提高加工效率。

［1］ Ye P Q，Shi C，Yang K M，et al.Interpolation of Continuous Micro Line Segment Trajectories Based on Look－ahead Algorithm in High－speed Machining［J］.International Journal of Advanced Manufacturing Technology，2008，37（9／10）：881－897.

［2］ Tsai M－S，Nien H－W，Yau H－Z.Development of a Real－time Look－ahead Interpolation Methodology with Spline－fitting Technique for Highspeed Machining［J］.Int.J.Adv.Manuf.Technol.，2010，47：621－638.

［3］ Wang H T，Zhao D B.Research and Implementation of NURBS Real－time and Look－ahead Interpolation Algorithm［C］／／2009International Conference on Measuring Technology and Mechatronics Automation.Zhangjiajie，2009：273－276.

［4］ 彭芳瑜，李黎.连续小直线段高速高精度插补中的动力学约束条件［J］.计算机辅助设计与图形学学报，2006，18（12）：1812－1816.

［5］ Cao Y N，Wang T M，Chen Y D，et al.High－speed Control Algorithm Using Look－ahead Strategy in CNC Systems［C］／／2008 3rd IEEE Conference onIndustrial Electronics and Applications.Singapore：2008：372－377.

［6］ 王宇晗，肖凌剑.小线段高速加工速度衔接数学模型［J］.上海交通大学学报，2004，38（6）：901－904.

［7］ 叶佩青，赵慎良.微小直线段的连续插补控制算法研究［J］.中国机械工程，2004，15（15）：1354－1356.

［8］ 董玉红，邵俊鹏，周室仁.CK7815数控机床进给伺服系统的建模及仿真［J］.哈尔滨理工大学学报，2005，10（3）：25－30.