基于真实接头车身概念模型的结构优化

宋 凯 成艾国 胡朝辉 钟志华

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

0 引言

传统的汽车车身概念模型大多采用具有等效特性的梁单元来模拟车身中的类梁形结构，用板壳单元组成车身大的覆盖面，用刚性单元或柔性的接头单元［1］来代替车身主要的接头结构。研究表明将接头作刚性处理可能使整车刚度增大50%～70%［2］，可见车身接头的刚度模拟十分重要。

计算机性能的快速提高以及高精度多参数近似模型的普遍应用已使概念模型的计算和优化时间不再是主要考虑的问题，那么概念模型中直接采用真实接头就成为一种较好的选择，其主要原因如下：

（1）传统概念模型采用柔性单元模拟接头时，需要提取接头的刚度。在提取接头刚度的过程中，接头几何中心点位置的选取和接头各个分支的截取长度对接头的刚度结果影响较大，容易产生较大误差；对于车身A柱下接头这类复杂的接头，提取刚度的工作量也较大。

（2）由于车身疲劳寿命的薄弱点一般在门框的角部区域，所以想要在概念设计阶段就考虑车身的疲劳耐久性能，就需要采用具有真实接头的概念模型。

（3）真实接头能准确地表达接头的质量，在概念模型的后续优化分析中可以将接头质量的变化考虑在内。

本文以国内某款自主研发的多功能乘用车为例，在其概念设计阶段首次建立了由真实接头并辅以梁单元和大尺寸壳单元组成的车身概念模型。

1 真实接头车身概念模型的建立

汽车车身的特性主要由车身关键截面特性、车身接头特性以及车身的框架结构特点决定，图1给出了基于真实接头车身概念模型（简称ZJ）的汽车车身设计流程。

图1 基于ZJ的汽车车身设计流程图

1.1 车身关键截面特性数据库

典型的车身关键截面一般是由若干层冲压钣金件通过焊接边上的若干焊点连接而形成的封闭截面，图2所示为某车型门槛梁典型截面。根据车型的不同，车身关键截面定义的位置也稍有差别，图3给出了某车型车身关键截面的位置。

图2 车身典型关键截面示意图

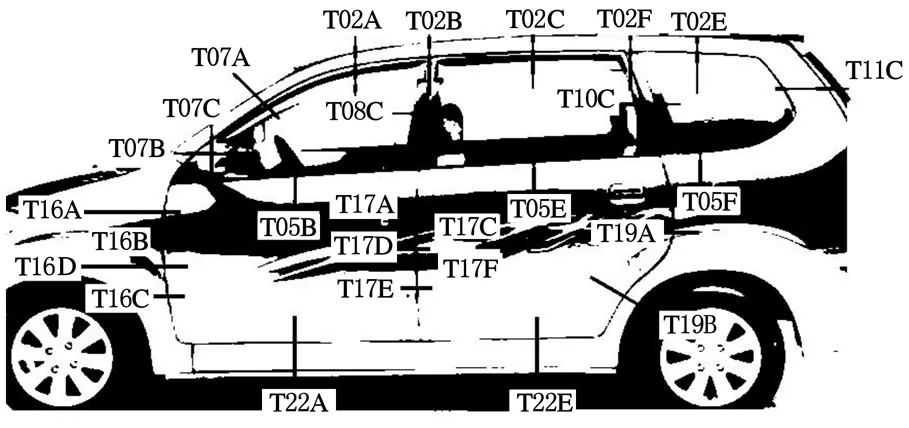
图3 车身关键截面位置示意图

车身关键截面特性数据库是一个汇聚了各种车型各个关键截面特性的综合信息库，它包含了各个截面的形状和位置，截面中每层零件的厚度及材料，截面的材料面积S，截面惯性矩Iy、Iz，截面惯性积Iyz，截面扭转常量Tj，截面所包围的总面积A等，它是设计厂家日积月累形成的核心资料。

1.2 车身真实接头数据库

接头是车身结构的关键过渡部分，其结构往往比较复杂，一个合理的接头结构不仅可以增加车身的刚度，而且可以提高车身的疲劳耐久特性，图4给出了某车型典型的接头位置示意图。

图4 车身典型接头位置示意图

要建立真实接头数据库，首先要确定如何截取接头部分，由于不同车型的接头结构可能差别较大，故对于接头的截取就不能简单地规定各个分支的截取长度，而要遵循几个原则：首先，尽量保留接头的特征和各个分支的圆角过渡部分；其次，尽量保留接头中的加强板结构。图5为某车型B柱下端接头的截取效果图。

图5 某车型B柱下端接头截取效果图

1.3 ZJ的建立与验证

在国内某款自主研发的多功能乘用车概念设计阶段，进行前期CAE分析的输入条件只有该车的外造型面、整车的总布置尺寸等，详细的车身有限元模型较难建立，需要建立概念模型。本文根据该车型的整体尺寸和基准车的结构特点，组合调用车身截面数据库和接头数据库中相应的数据，利用MSC.Patran软件建立的真实接头车身概念模型如图6所示。模型总长4200mm，总宽度1600mm，总高度1700mm；车身主要的承载结构，如A柱、B柱、C柱、D柱、门槛梁、顶盖周边梁、车架前后大梁和地板横梁等采用薄壁梁单元模拟，模型中梁单元共364个，有38种不同规格的截面特性；主要板壳承载部件，如地板、顶盖、前后轮罩、后侧围和防火墙等采用板壳单元模拟，模型中该类大尺寸壳单元共1110个；对车身结构性能影响较大的关键接头，如A柱、B柱、C柱、D柱的接头采用参考车或基型车的真实接头有限元模型代替，模型中真实接头左右对称共计14个；ZJ中共计810 24个节点，772 44个单元。概念模型中，梁单元与接头的分支通过RBE2单元连接，梁单元和壳单元通过共节点连接；真实接头中各个零部件采用CWELD单元模拟点焊，采用RBE2单元模拟二氧化碳保护焊。

图6 ZJ示意图

有研究表明，详细车身有限元模型中局部采用梁单元代替相应的详细结构，其精度是可以满足工程需要的［3］。本文建立的ZJ特性如表1所示，从表中可以看出，ZJ的各种参数和该车型最终的详细有限元模型参数比较接近，说明本文建立的概念模型满足前期工程应用的精度要求。由于最终的详细有限元模型是在概念模型的基础上通过优化设计和局部调整后得到的，所以本文的ZJ和最终详细有限元模型的特性会有一定的误差。

表1 详细有限元模型和ZJ特性对比

2 近似模型的构建

近似方法是一种计算效率高、能较大程度加快优化过程且可靠性较高的优化设计方法，它的数学本质是利用逼近近似技术对离散数据进行拟合或插值来实现对未知点响应的预测，它是实验设计、数理统计和最优化技术的一种综合。

2.1 拉丁方试验设计

在整个设计空间选取有限数量的样本点，使之尽可能地反映设计空间的特性，即称为试验设计［4］，它是构建近似模型必不可少的步骤。本文采用拉丁方试验设计，它是一种充满空间的设计，它使输入组合相对均匀地填满整个试验区间，每个因素的设计空间都被均匀划分，并且所有因素都有同样数目的分区。然后，所有这些水平随机地组合在一起，同时，每一个因素的每个水平只被研究一次，这样就形成了采样点的设计矩阵，由于每个因子在每个水平上都能得到均匀地应用，因此，拉丁方试验设计能够以较少的样本点反映整个设计空间的特性，是一种有效的样本缩减技术，具有效率高、均衡性能好的优点［5］。

2.2 移动最小二乘响应面法

响应面方法作为目前应用最为广泛的近似方法，它是一种以试验设计为基础的用于处理多变量问题建模和分析的一套统计处理技术，其实质是以试验设计、经验公式或数值分析为基础，对设计空间内的设计点的集合进行连续的试验求值，构造目标和约束的全局逼近。在工程应用领域，多项式响应面模型应用比较广泛，本文采用移动最小二乘二阶多项式响应面模型，其基本理论可简述如下：

式中，xi为设计变量；y为响应面拟合函数；m为设计变量的个数；β0、βi、βii、βij为待定系数。

对式（1）进行多元线性回归处理，即

一般设ε～ N（0，σ2）。对于待定系数βk（k＝0，1，…，r），利用M（M ≥r＋1）个样本点采用移动最小二乘法确定，通过对加权余量函数求极小值获得。加权余量函数定义为

式中，yI为第I个样本点的响应值；＾yI为第I个样本点的近似值；W（x－xI）为样本点xI在兴趣域Ωx内任意点x的权函数，它必须保证近似的局部性和连续性。

式中，s＝d／dmax；d为任意点x与采样点xI之间的距离；dmax为紧支子域的半径。

通常的权函数有指数型函数、三次样条函数和四次样条函数等，这里选用四次样条函数作为权函数：

2.3 响应面模型构建

2.3.1 白车身静态扭曲刚度分析模型的描述

在汽车行驶的过程中，车轮受到路面激励而使车身发生扭转变形的情况很普遍，车身抵抗扭转变形的能力将直接影响到车身的疲劳寿命及乘坐的舒适性。车身扭转刚度K反映了车身抵抗扭转变形的能力，该指标是车身常用刚度指标之一。

本文在白车身左右前悬中心点施加一对方向相反的z方向力F，约束左右前悬连线中点的平动自由度及车身后悬支点区域的平动自由度，此时，扭转刚度K为

式中，M′为加载的扭矩；θ为左右前悬中心连线的扭转角；δz为右前悬中心点z向位移值；F为每个前悬中心点的加载力（本文取值2000N）；Y为右前悬中心点y的坐标值（本文为577.8075mm）。

2.3.2 整车准静态强度分析模型的描述

汽车整车多工况准静态强度分析方法是常用的车身强度分析方法，该方法简述如下：根据车辆道路行使过程中车身各工况的加速度情况，计算出车辆4个轮胎处的路面载荷，将轮胎处的载荷通过车辆悬架的ADAMS模型转化为车身硬点处的载荷，将车身硬点处的载荷加载到整车（配重至满载状态）有限元模型，通过NASTRAN的惯性释放方法计算车身在各种工况下的应力情况。如图7所示，以ZJ为基础将整车中的动力系统、传动系统、排气系统、空调系统、座椅、乘员、车门、油箱、备胎和仪表板等非结构质量连接到白车身模型上，将整车有限元模型配重至满载设计要求的1600kg（不包含簧下质量）。

图7 满载状态整车有限元模型

本文选取车辆行驶过程中较为典型的过坑扭曲工况，重点关注白车身中各个真实接头的最大应力区域。

2.3.3 选择设计变量

在ZJ中，车身的类梁形结构由具有等效特性的梁单元模拟，而梁单元的特性（除它本身在整车坐标系中的位置）可以用截面的材料填充面积S，截面惯性矩Iy、Iz，截面惯性积Iyz，截面扭转常量TJ这5个参数表示。实际工程中车身关键截面的各种特性之间有较强的关联性。本文引入Donders等［6］提出的截面等效厚度T的概念，使截面的各个特性随等效厚度产生线性关联变化，其原理可简述如下：由于车身中大多关键截面具有类矩形特征，故该方法假设车身关键截面形状可表示为图8所示的壁厚为T的矩形，其截面特性经过简化可表示为矩形壁厚T的线性函数：

式中，矩形宽度b≈b1，矩形高度h≈h1。

本文将ZJ中关键截面等效厚度和真实接头中的加强板厚度作为变量，将白车身的扭转刚度K，受力较大的接头3、接头5、接头6、接头7的最大应力σ3、σ5、σ6、σ7和白车身质量mc作为响应量。由于车身变量较多，需要进行灵敏度分析以减少变量数目。如图9所示，首先根据实际工程经验初选模型中的33个截面（左右对称）的等效厚度变化率r（r为优化的截面等效厚度与初始的截面等效厚度之比）和7个接头（左右对称）中的加强板厚度t作为变量，然后对6个响应量分别进行灵敏度分析。表2列出了每个响应量敏感度最高的5个变量名称，最终选取的优化设计变量共10个，将它们作为两个分析模型的耦合设计变量，各个设计变量的初始值及取值范围见表3。

表2 每个响应量敏感度最高的5个变量

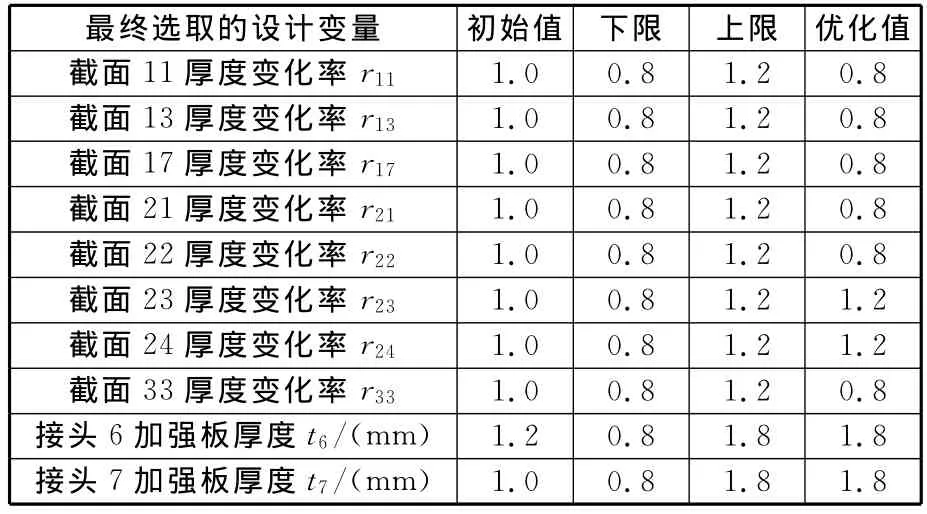
表3 设计变量初始值、取值范围和优化结果

2.3.4 移动最小二乘响应面模型构建

本文将每个设计变量平均分成70个设计水平，利用拉丁方试验设计方法进行70次采样。设置设计变量为r11、r13、r17、r21～r24、r33、t6、t7，将车身扭转刚度K和真实接头中受力较大的接头3、接头5、接头6、接头7的最大应力σ3、σ5、σ6、σ7作为约束函数，将车身的总质量mc作为目标函数构建其优化问题的近似模型：

其中，σ3、σ5、σ6、σ7的应力约束值是针对 DC03材料（弹性模量E＝210GPa，泊松比μ＝0.3，密度ρ＝7850kg／m3，屈服强度σs一般在120MPa至240MPa之间，抗拉强度σb≥270MPa）按照指定的车身疲劳寿命计算得出的，其中σ6、σ7的约束值根据实际工程经验适当放大。

2.4 响应面模型精度评价

近似模型需满足必要的精度才能够替代有限元模型进行优化计算。检验响应面模型精度可从两个方面进行：其一是检验响应面模型在采样样本点时的拟合相对误差；其二是检验响应面模型在设计空间中任意点的相对误差。相对误差RE的表达式为

式中，y为有限元模型仿真计算值；˜y为响应表面预测值。

图10为接头6最大应力σ6在70个样本点处的相对误差示意图，各个响应量在采样点的最大相对误差如表4所示。本文在设计空间中随机选取了5个样本点，各个响应量在任意样本点的相对误差如表5和表6所示。由表4～表6的数据可以看出，各响应量的相对误差绝对值大都在2%以内。综上所述，本文构建的响应面模型精度较好，可以代替真实有限元模型进行优化计算。

图10 接头6最大应力σ6采样样本点相对误差

表4 各响应量采样样本点最大相对误差

表5 任意样本点相对误差（一）

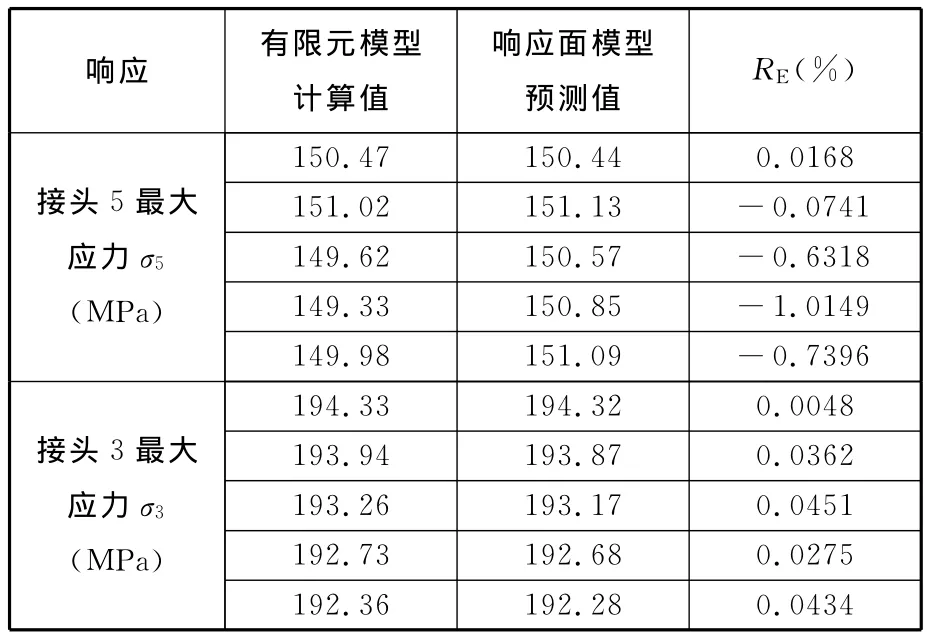
表6 任意样本点相对误差（二）

3 ZJ优化分析

在汽车概念设计阶段，车身结构变动的余地较大，车身关键截面和关键部件厚度等参数取值范围经常发生变化，要得到工程师比较满意的结果往往需要进行大量反复的优化计算，且本文ZJ的约束目标函数牵扯到两个计算模型，若每次都采用物理模型进行优化计算，则效率将会很低。因此，笔者构建近似模型来替代物理有限元模型进行优化分析，ZJ优化设计流程如图11所示。

图11 ZJ优化设计流程图

图12 目标函数mc的优化过程

利用连续二次规划优化算法对上述近似模型进行优化，目标函数mc的优化过程如图12所示，各个变量的优化值见表3，将变量优化值代入有限元物理模型计算的结果及响应面模型优化结果见表7。

表7 各响应优化前后结果对比

通过优化分析，ZJ的B柱上接头、C柱上接头、D柱上下接头区域在整车过坑扭曲工况下的最大应力满足了给定指标，车身的扭转刚度K也有了较大提高，并且白车身总质量减轻了6kg左右。

根据优化结果可知，D柱上下接头的加强板优化厚度都有所增厚，这是由于该车型尾门框接头在车辆行驶过程中受载荷较大，其应力水平主要和尾门框的局部刚度有关，在不改变尾门框大小的前提下，通过增加加强板厚度来提高刚度是最为有效的方法。根据灵敏度分析结果可知，B柱上接头和C柱上接头的加强板对该接头最大应力不是影响最显著的，这是由于B柱上接头、C柱上接头处于车身的中部，其受载情况和整个车身的刚度有较大关系，若能使车身均匀受载，即使不增加其加强板的厚度也能使其应力降低。根据优化得到的车身关键截面特性，考虑车身造型、内部空间以及总布置等方面的尺寸约束条件，同时考虑截面钣金件冲压成形等方面的形状约束要求，通过蚁群算法可以快速生成较为合理的截面形状，这里不再赘述。

通过在概念设计阶段就利用ZJ对车身敏感部位进行优化设计，从而减小了详细设计阶段的设计更改工作量和缩短了研发周期。该方法和现行商业软件SFE Concept相比，ZJ模型更加易于构建，对工程师的技能要求不高，计算效率也相对较快，且精度完全满足前期工程的应用需要，但是由于不是全参数化模型，所以对于模拟白车身整体结构框架形式的变形能力较弱。该车型最终状态的白车身有限元模型如图13所示，白车身参数如表1所示，白车身的刚度和模态指标均达到了设计要求，且该状态车身结构顺利通过了海南试验场26 000km的强化道路试验，目前该车型已进入量产阶段。

图13 最终状态的详细有限元模型

4 结论

（1）首次提出了适用于汽车概念设计阶段的由真实接头并辅以梁单元和大尺寸壳单元组成的车身概念模型。通过某自主研发的多功能乘用车应用案例，表明ZJ是一种易于构建、修改方便且满足工程应用精度要求的有效模型。

（2）在某自主研发的多功能乘用车概念设计阶段，建立了ZJ的强度分析模型和刚度分析模型，利用拉丁方试验设计方法和移动最小二乘响应面法构建了其近似模型，通过连续二次规划优化算法得到了车身截面特性和真实接头加强板厚度的合理组合，实现了车身的轻量化，为该车型的后续设计工作提供了重要的支持。

［1］ 黄金陵，娄永强，龚礼洲.轿车车身结构概念模型中接头的模拟［J］.机械工程学报，2000，36（3）：78－81.

［2］ Chang D C.Effects of Flexible Connections on Body Structural Response［J］.SAE Transactions，1974，83：233－244.

［3］ Mundo D，Hadjit R，Donders S，et al.Simplified Modeling of Joints and Beam－like Structures for BIW Optimization in a Concept Phase of the Vehicle Design Process［J］.Finite Elements in Analysis and Design，2009，45：456－462.

［4］ 刘文卿.试验设计［M］.北京：清华大学出版社，2005.

［5］ 张勇.基于近似模型的汽车轻量化优化设计方法［D］.长沙：湖南大学，2009.

［6］ Donderso S，Takahashi Y，Hadjit R，et al.A Reduced Beam and Joint Concept Modeling Approach to Optimize Global Vehicle Body Dynamics［J］.Finite Elements in Analysis and Design，2009，45：439－455.