电场活化聚合物卷筒型致动器设计方法研究
陈 娟 刘 琨 吕新生 张 晔
合肥工业大学,合肥,230009
0 引言
电场活化聚合物(DE)是一种能够在电流、电压或电场作用下产生物理形变的聚合物压电材料,这种形变具有瞬发性(微秒级),因此被视为微型机器人致动器乃至人造肌肉的理想材料。作为新一代的聚合物材料,电场活化聚合物能够对电的刺激表现出足够强的物理响应,具有应变量大、响应快、效率高等特点,可以应用于新型致动器以及新型传感器和发电机装置中。电场活化聚合物的独特特性能够从根本上影响新型致动装置的发展。近十年来,各国学者对该材料的性能进行了深入的理论和实验研究,特别在驱动材料方面[1-4]。在对电场活化聚合物变形特性的研究基础上,通过分析电场活化聚合物的驱动原理,分别设计出一维伸缩、平面弯曲、空间弯曲等卷筒型致动器,使其具有大的力输出、变形输出和较高的效
1 电场活化聚合物的驱动机理
1.1 驱动原理
处于电场中的弹性体沿电力线的方向收缩,同时沿垂直于电力线的方向膨胀,这种现象被称为麦克斯韦应力现象,也是电场活化聚合物致动器的基本作用原理[1]。如图1所示,沿电力线方向的有效作用(压)力p为
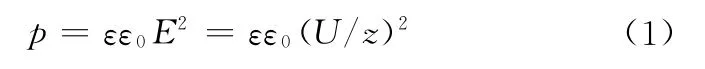
式中,ε为相对介电常数,F/m;ε0为真空介电常数,ε0=8.85×10-12F/m;E为电场强度,N/C;U为施加电压,V;z为电力线方向的材料厚度,mm[5]。

图1 麦克斯韦应力现象
与传统微驱动材料相比[6],电场活化聚合物比传统的脆性压电陶瓷产生的应变高出两个数量级,比形状记忆合金响应速度更快,因而成为国内外瞩目的新型微驱动材料。
1.2 预拉伸在电场活化聚合物变形中的作用
实验结果表明,电活化聚合物材料在加电压之前进行均匀预拉伸(图2a),将会提高材料的力学性能,即预应变越大产生的变形率更大。因此,预拉伸对材料在平面内的(面积扩大)变形起到了诱发和引导的重要作用。
当x、y两个方向的预拉伸比例不一样时,会出现大面积褶皱(图2b),褶皱纹理的走向为预拉伸小的方向,图像有呈现椭圆形状的倾向,这种不均匀预变形对材料的变形起到了一定的阻碍作用;而在没有预拉伸变形的情况下,变形的响应速度明显降低,图像表现为电极涂敷范围内材料凸起成半球面状(图2c)。

图2 不同预拉伸状态下的变形图
预拉伸的另一重要作用是提高抗电击穿能力。预拉伸比例越大,所能承受的极限电压越高(图3)[7],这说明预拉伸不仅能加快电场活化聚合物在电场力作用下的响应、提高变形率、减小工作电压,而且可大幅度增强其抗电击穿破坏的能力。

图3 预变形和单位厚度上极限电压的关系
2 致动器设计方法研究
目前比较实用的电场活化聚合物致动器结构类型大致可分为领结型、卷筒型和管型。其中卷筒型致动器的最大输出力比领结型致动器的最大输出力大,因而更适用于仿生机器及医疗等领域。卷筒型致动器结构特点是:采用弹簧元件提供预拉伸力;采用多层膜加大输出力。通常所采用的弹簧元件是圆柱弹簧,用数层已经覆盖上不同排列模式的屈从电极的电场活化聚合物薄膜包裹在弹簧周围,通电后可以使圆筒伸长或弯曲,如图4所示。

图4 卷筒型致动器
2.1 一维伸缩致动器
卷筒型一维伸缩致动器主要由电场活化聚合物薄膜(双层重叠)、预拉伸微调装置、圆柱螺旋压缩弹簧、弹簧导杆以及防护罩等几个主要部分组成,如图5所示[8]。

图5 卷筒型一维伸缩致动器结构图
2.1.1 一维伸缩致动器的力学模型
卷筒型一维伸缩致动器在工作状态下主要受到两个力的作用:一个是预拉伸力与加载电压以后的麦克斯韦应力的合力f0,另一个是弹簧受压缩后产生的弹性恢复力。当f0小于时致动器伸长;当f0大于时致动器缩短;当两者相等时致动器处于稳定状态。对于可利用公式=kx计算,这里重点讨论预拉伸力与加载电压(5500V)以后的麦克斯韦应力的合力f0。
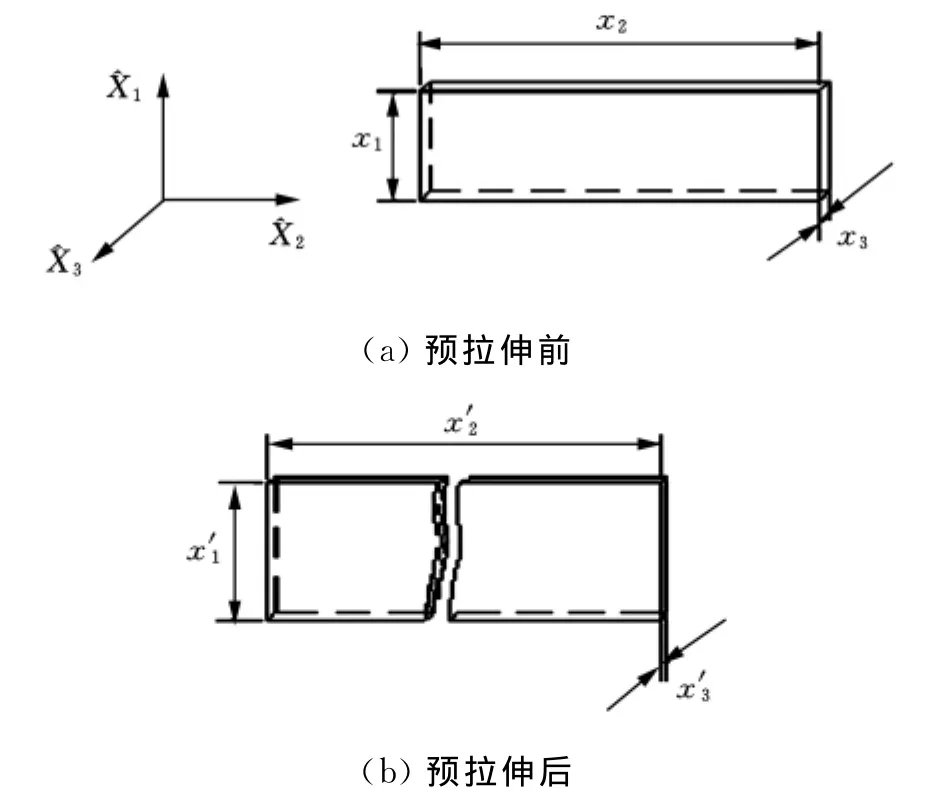
图6 DE薄膜预拉伸前后尺寸

式中,Y1为电极直线方向变形率;X(1)~X(4)依次为经过规格化处理的电压、预拉伸率、窗口直径、电极厚度值。
直线方向变形量则为

2.1.2 实验结果与分析
根据实验数据处理方法获得致动器位移(伸长)的实验值,该实验值与理论设计值不一致,导致这种差值的原因是:周向预拉伸力不能得到保持,从而出现图4所示的颈缩现象。
2.2 平面弯曲致动器
平面弯曲致动器是将电场活化聚合物膜片两面涂上屈从电极,卷成圆筒状,两端粘接在上下固定座上(图7),且圆周上两侧电极涂抹范围都小于180°,上下固定座之间的螺旋压缩弹簧使膜片获得一个轴向的预加应变,为防止致动器出现颈缩现象,设置了周向预拉伸力保持环及其安装工具。通电后卷筒在每一侧获得一个独立的致动运动:如果左半边通电,右半边保持断电,结果是左侧膜片伸长,造成整个卷筒(包括弹簧)向右弯曲;如果右半边通电,则整个卷筒向左弯曲;如果左右两侧同时施加相同的电压,则整个卷筒伸长,相当于一维伸缩致动器[10]。

图7 平面弯曲致动器结构图
2.2.1 平面弯曲致动器的力学模型
如图8所示,平面弯曲致动器受到3个力的作用:左右两侧膜片预拉伸后产生的恢复力与加载电压以后产生的麦克斯韦应力的合力F21和F22,以及弹簧受压缩后产生的弹性恢复力F1。有如下力平衡关系存在:F1=F21+F22。① 当F21=F22时无力矩;②当F21≠F22时产生力矩M,M = (F21-F22)R,使弹簧产生横向弯曲。

图8 平面弯曲致动器的力学模型
2.2.2 圆柱螺旋弹簧的横向弯曲刚度及其挠度、转角的计算
根据致动器结构特点,将弹簧视为当量悬臂梁建立弹簧横向刚度及其挠度、转角的计算模型,弹簧的下端为刚性固定,上端可在横向自由运动(移动或转动),承受轴向力P、横向剪力Q和力矩M。首先暂不考虑剪切变形的影响,当梁的跨度远大于横截面时,忽略剪力Q对变形的影响,则可得到横力弯曲变形公式[11]:
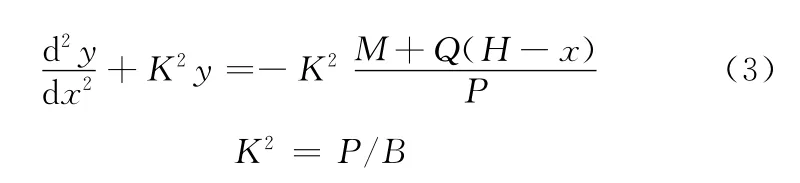
式中,B为当量悬臂梁的弯曲刚度;H为柱螺旋弹簧的高度。
经过一系列的推导,当量悬臂梁的自由端最大位移δx、转角γH的公式分别为

从而可以计算得到不同电压下的弯曲变形,计算结果如表1所示。
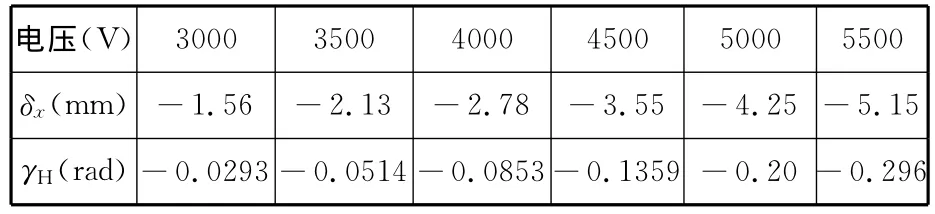
表1 不同电压下致动器的端部横向挠度和转角
采用上述弹簧圆筒结构,如果驱动器是用周围均匀布置4片或6片等DE薄膜的弹簧来构造的,则正对的两片DE薄膜成对作用构成一弯曲驱动器,即DE薄膜中的一片施加电压时,该侧薄膜将伸长带动弹簧向另一侧弯曲。适当控制相应的薄膜通断电方式,即可实现驱动器沿弹簧轴线伸长和多个不同方向的转动。
2.3 多维复合致动器
基于上述基本致动元件的组合可以实现许多复杂运动,如利用多个一维伸缩致动器构成可操纵的医用导管和蛇形机器人[12],利用多个二维弯曲致动器构成能在崎岖路面前进的六腿机器人等。本文着重介绍一种利用两个一维伸缩致动器构成的平面转角致动器。平面转角驱动器的结构如图9所示。工作原理如下:两个一维伸缩致动器一端固定,另一端通过绳索与带有指针的定滑轮连接,与前面介绍的一维伸缩致动器不同的是,这里所用的一维伸缩致动器中没有弹簧,即不是通过弹簧提供的轴向预拉伸力,而是通过调节滑轮中心与两个一维伸缩致动器的(垂直方向)相互位置提供的轴向预拉伸力;两个一维伸缩致动器分别受到预拉伸力与加载电压以后的麦克斯韦应力的合力F1、F2,当两者相等时致动器处于稳定状态,指针不发生偏转,当一侧或两侧一维伸缩致动器所加电压发生变化造成F1大于或小于F2时,指针都将发生偏转。
2.3.1 平面转角致动器力学模型
对这一过程的数学描述如下:

图9 平面转角致动器结构图
(1)当F1-F2>0时,指针发生偏转,有

式中,F1、F2根据Ogden公式计算;J为转动惯量;R为滑轮半径。
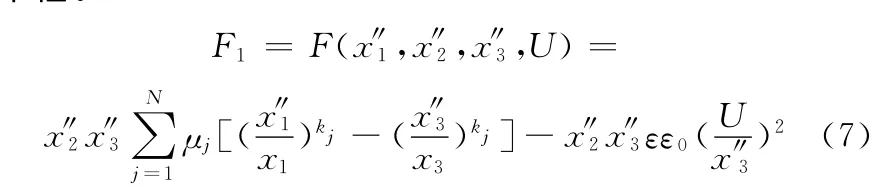
其中,kj、μj是材料常数,1<N ≤3,F2的计算公式与F1相同。
(2)当两侧绳索长度发生一增一减变化时(这里假设绳索本身不可伸长,即绳索总长度不变,一边绳索的加长量等于另一边绳索的减短量),膜的轴向尺寸发生变化,由于膜的体积不变,也要发生相应变化,从而导致F1、F2发生变化,考虑到电场活化聚合物材料特性的非线性,可以通过微增量逐步迭代计算变化后的F1、F2,即给定绳索长度(也即膜轴向拉伸量)增减的微增量dx,计算出两侧获得微增量后的(下式中x的下标代表不同侧一维伸缩致动器):


式中,Δl为单边绳索的总伸长(缩短)量。
两侧一维伸缩致动器所加电压的差值不同,指针的偏转量也相应地不同,从而可得出卷筒型平面转角致动器偏转角度随电压差值变化的特性曲线。
2.3.2 平面转角致动器的性能模拟
根据上述公式,用FORTRAN语言编写仿真程序,程序流程如图10所示。
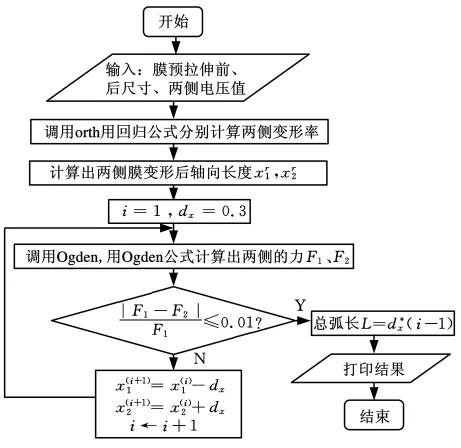
图10 程序流程图
设膜的原始尺寸x1=10mm,x2=60mm,x3=1.2mm, 预 拉 伸 后 的 尺 寸x′1=30mm,x′2=180mm(预拉伸率200%×200%),滑轮半径R=10mm,一侧电压保持3000V不变,另一侧电压发生变化,用上述程序求得两侧电压不同情况下指针所偏转的角度,如表2所示。
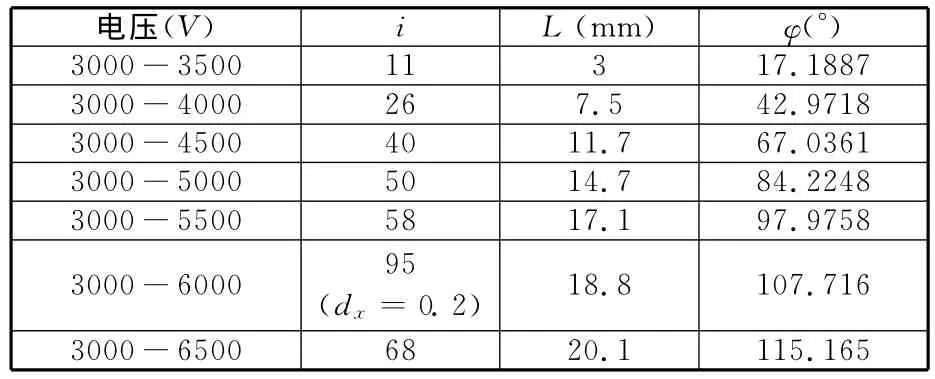
表2 不同电压时滑轮转动的角度
从而可得出卷筒型平面转角致动器偏转角度随电压差值变化的特性曲线,如图11所示。可见该平面转角致动器可以实现预期的平面转动。
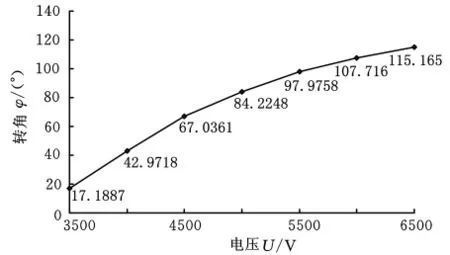
图11 偏转角随电压值变化特性曲线
3 结束语
本文阐述了基于电场活化聚合物材料的卷筒型致动器设计方法,介绍了各种致动器的工作原理、力学模型,数值模拟结果表明:所设计的一维伸缩致动器、平面弯曲致动器、平面转角致动器都可以实现预期的运动,从而为此类致动器的进一步设计研究打下了重要基础。
[1] Halloran A O,Malley F O.Materials and Technologies for Artificial Muscle:A Review for the Mechatronic Muscle Project[R].Galway:National University of Ireland Galway,2004.
[2] Pelrine R,Sommer-Larsen P,Kornbluh R,et al.Applications of Dielectric Elastomer Actuators[C]//Proceedings of SPIE.San Diego,CA,2001:335-349.
[3] Kofod G.Dielectric Elastomer Actuators[D].Denmark:The Technical University of Denmark,2001.
[4] Federico C,Alberto M,Danilo de R.High-strain Dielectric Elastomer for Actuation[C]//Proceedings of SPIE.Seattle,WA,2002:419-422.
[5] Pelrine R,Kornbluh R,Joseph J.Electrostriction of Polymer Dielectrics with Compliant Electrodes as a Means of Actuation[J].Sensors and Actuators A,1998,64(1):77-85.
[6] 陈娟.基于二次正交回归实验的电场活化聚合物变形特性的建模与仿真研究[D].合肥:合肥工业大学,2006.
[7] 陈娟,赵翠清,祁新梅,等.电场活化聚合物实验研究[J].高分子材料科学与工程,2007(4):103-104.
[8] 李刚,冯敏亮,吕新生.基于电场活化聚合物(DE)的一维伸缩致动器设计[J].机械工程师,2000(8):100-102.
[9] 陈娟,吕新生,张晔.电场活化聚合物变形的建模与仿真[J].材料科学与工程学报,2007,35(3):2-6.
[10] 刘亚东,吕新生,张晔.电场活化聚合物(DE)平面弯曲致动器设计[J].机电一体化.2009(7):94-96.
[11] 米彩盈.一种确定高圆簧横向刚度的有效方法[J].西南交通大学学报,1998(3):294-298.
[12] Dickinson M H,Farley C T,Full R J,et al.How Animals Move:An Integrative View[J].Science,2000,288:100-106.

