一种求解多孔边裂纹板应力强度因子的解析方法

赵晋芳 谢里阳 刘建中 赵 群

1.东北大学，沈阳，110004 2.北京航空材料研究院，北京，100095 3.沈阳工程学院，沈阳，110136

0 引言

在众多的孔口问题，特别是一些形状比较复杂的单孔口问题上，复变函数在求解其应力强度因子时，都体现出了一定的优越性［1－4］，如文献［5］研究了带裂纹的方形孔口问题，文献［6］研究了带裂纹的圆形孔口问题。但以上文献大都是对各种单孔口问题的应力强度因子进行研究，对于多孔口问题的研究尚不多见。较为典型的共线多孔边裂纹结构常见于老龄飞机外蒙皮的铆钉孔边处，这种结构会对飞机的结构安全性形成极大威胁，因此求解其应力强度因子，认识其发展变化规律有着十分重要的意义［7－9］。

本文介绍了一种求解多孔边裂纹板应力强度因子的解析方法。首先利用复变函数性质确定单孔裂纹板的复变应力函数，再运用复变函数的近似迭加法［10］求解出多孔边裂纹板的应力强度因子。通过与有限元结果的比较可知，这种解析方法在此类问题的求解上具有较高精度，而且相比有限元方法［11－12］更加省时。

1 基本原理

1.1 Muskhelishvili复变函数法

对于一般的弹性力学平面问题，当不计体力时，其应力分量和位移分量可以由复变解析函数Φ（z）、Ψ（z）决定，表示为

式（1）为平面应力情况。对于平面应变情况，只要将式中的E换为即可。

为了便于讨论边界条件，引入辅助平面ζ，于是z平面与ζ平面之间存在变换关系：z＝ω（ζ）。将Φ（z）、Ψ（z）看作ζ的解析函数，则有

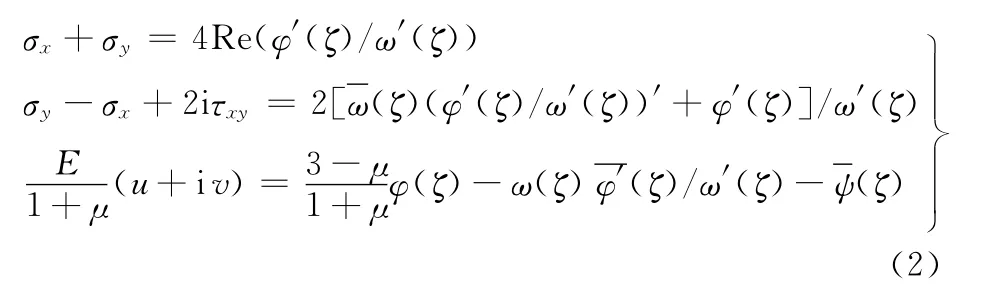
式中，φ（ζ）、ψ（ζ）为应力函数。

在无限大的多连体中，欲保证结构为平面应力状态，则在ζ平面上的应力函数表达式为

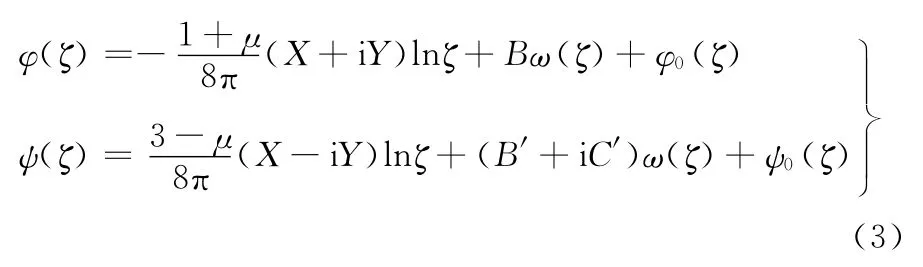
其中，X、Y分别是有限边界上沿x、y方向上的面力之和，B、B′、C′由无限远处的应力条件决定，φ0（ζ）和ψ0（ζ）为未知函数，作补充项用于求解应力函数。经边界条件变换后，函数φ（ζ）和ψ（ζ）在弹性体的边界上必须满足：

式中，［］s表示沿边界s积分。

在单位圆边界上作极坐标（ρ，θ）变换，由于ρ＝1，因而ζ＝ρeiθ＝eiθ，引入记号σ＝eiθ，则式（4）可以写成

取式（3）的边界值，则有

则φ0（ζ）的边界条件可以写成：

上述过程是将物体映射到ζ平面上单位圆外部的复变应力函数推导过程。在确定φ0（ζ）后，可由式（3）确定φ（ζ），再由式（2）求得相应的应力分量和位移分量。

对于求解二维复合型裂纹的应力强度因子，可由下式分离得到相应的KⅠ和KⅡ：

式中，KⅠ为Ⅰ型裂纹的应力强度因子，KⅡ为Ⅱ型裂纹的应力强度因子。

1.2 单孔边裂纹问题的复变应力函数

解决单孔边裂纹问题的关键一步就是建立保角映射函数。设有一含有孔边不对称裂纹的无限大平面，圆孔半径为a，裂纹长分别为b－a和c－a，如图1所示。以圆孔中心为原点，以裂纹所在直线为x轴建立直角坐标系，作保角映射：

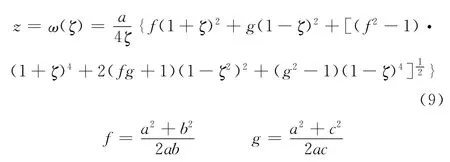
图1 物理平面上含孔边不对称裂纹的无限板到数学平面上单位圆外部的映射

该映射将物理平面上含单孔边不对称裂纹的无限板保角映射到数学平面上单位圆的外部，且有ω－1（b）→ 1，ω－1（－c）→－1，ω－1（ai）→ B，ω－1（－ai）→B1，同时把a的上岸映射到点A，把a的下岸映射到点A1，把－a的上岸映射到点C，把－a的下岸映射到点C1。

显然，ω（ζ）有且只有一个一级极点ζ→ ∞。计算

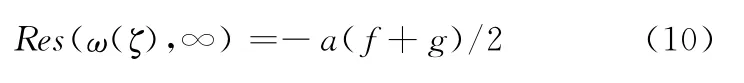
其中，Res表示留数，对映射函数求导有

现在假设该无限板在y轴方向受到均匀外力q作用，孔口不受力，于是有

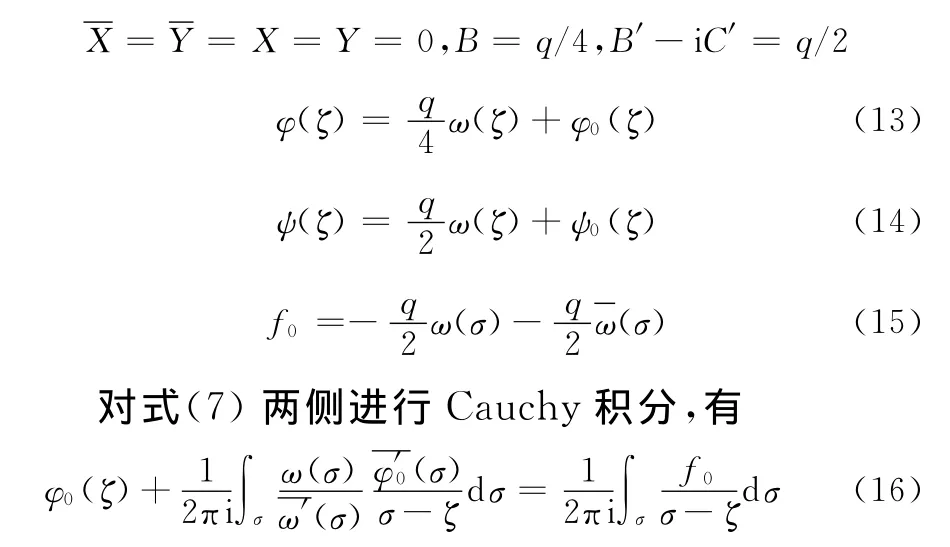
将式（15）代入式（16），得

则H（ζ）是在单位圆外的解析函数，且为圆周上的连续函数。由无穷远处Cauchy积分公式，式

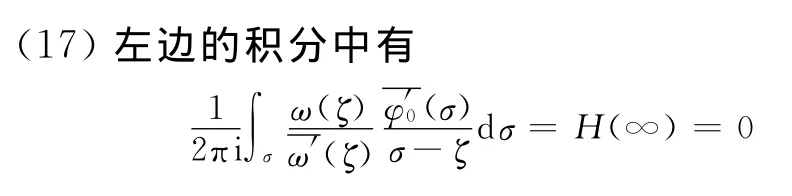
因此，式（17）可简化为

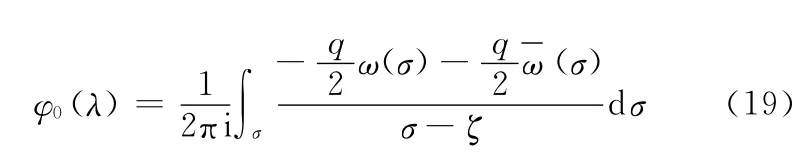
因为ζ→ ∞是ω（ζ）和ω1（ζ）的一级极点，由留数定理有

将式（20）、式（21）、式（10）代入式（19），得

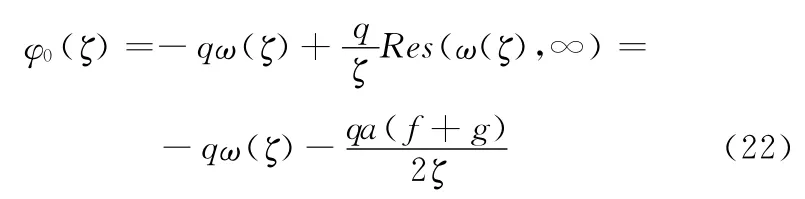
将式（22）代入式（13），得

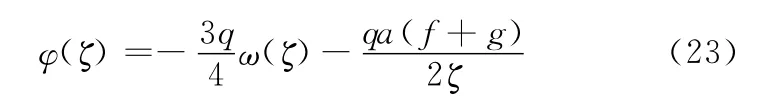
这样便完成了对φ（ζ）的求解。

1.3 复变应力函数的近似迭加法

对于多孔边裂纹问题（图2所示为两孔结构），可以运用复变应力函数的近似迭加法进行计算，即孔口1裂纹尖端P点的应力强度因子应迭加其他孔口对P点应力强度因子的影响，即

其中，φ1为孔口1的复变应力函数，ζ1为孔口1局部坐标中裂纹尖端P的坐标，其余各项的应力函数φ2、φ3…表示相应孔口对孔口1裂纹尖端P点应力场强度的影响项。显然，复变应力函数φi应满足各自孔口i的应力边界条件，应满足无限远处的应力条件。于是，的各项可以通过无限板上仅有第i个孔边裂纹时的解求出，并除去其中表示无限远边界条件的影响项。

图2 含多孔边裂纹的无限板

在式（24）中，ζi是裂纹尖端P 点在第i个孔口的局部坐标中的相应值，可由变换函数z＝ωi（ζi）的反函数ζi＝fi（z）求得。

2 数值算例

本部分计算了无限板上含共线双孔对称裂纹的情况，并将解析结果与有限元结果进行了比较。由于结构的对称性，双孔内侧两条裂纹的应力强度因子相等，双孔外侧两条裂纹的应力强度因子亦然，因此图3只给出了Tip1和Tip2的解析结果及有限元结果。

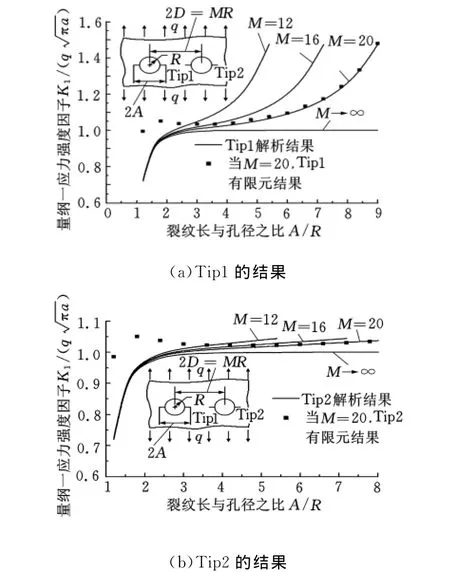
图3 无限板共线双孔对称裂纹的SIF值

通过比较表明，这两种计算结果比较一致，特别是在裂纹长与孔径之比A／R较大时，两者基本一致。因为本文构造的保角函数是一个超越函数，即不满足任何以多项式作为系数的多项式方程函数，所以该映射函数和传统方法中通过截项获得的由许多项组成的多项式映射函数有些许不同，这便导致了在A／R较小时，解析结果与有限元结果有所差异。不过，人们较为关注的是多孔边裂纹在贯穿或合并的瞬间以及在此之前的时刻，因此这种解析方法在解决实际的工程断裂问题中有一定的适用性。

3 结论

文章提出了一种求解无限板多孔边裂纹应力强度因子的解析方法，方法主要分为两个部分：①利用解析函数性质求解无限板单孔边裂纹的复变应力函数；②利用复变应力函数的近似迭加法逐一将其他裂纹对所求裂尖应力场强度的影响迭加上去，从而得到无限板多孔边裂纹的应力强度因子。这种方法不但简化了传统求解方法中通过截项法找到近似应力函数的繁琐步骤，而且将复杂的多位置损伤问题转化为简单的单位置损伤问题进行处理。计算过程简单、易行，计算结果精确、可靠。

［1］ Muskhelishvili N I.Some Basic Problems of Mathematical Theory of Elasticity ［M ］.Gorningen：Noordhoff，1953.

［2］ 徐芝纶.弹性力学［M］.北京：高等教育出版社，1990.

［3］ 范天佑.断裂理论基础［M］.北京：科学出版社，2003.

［4］ Shen Dawei，Fan Tianyou.Exact Solutions of Two Semi－infinite Cracks in a Strip［J］.Engineering Fracture Mechemics，2003，70：813－822.

［5］ Hacebe N，Yoshikawa K，Ueda M，et al.Planes Elastic Solution for the Second Mixed Boundary Value Problem and Its Application［J］.Archive of Applied Mechanics，1994，64：295－306.

［6］ 郭俊宏，刘官厅.具有不对称共线裂纹的圆形孔口问题的应力分析［J］.内蒙古师范大学学报（自然科学汉文版），2007，36（4）：418－422.

［7］ 倪惠玲.多处损伤特性的研究［J］.航空学报，1996，17（3）：302－309.

［8］ Goranson U G.Elements of Structural Intergrity Assurance［J］.Int.J.Fatigue，1994，16（1）：43－65.

［9］ Schijve J.Fatigue of Aircraft Materials and Structures［J］.Int.J.Fatigue，1994，16（1）：21－32.

［10］ Zhang Yongyuan，Zhao Yi.Stress Intensity Factors for Radial Cracks Around Circular Holes—method of Evaluation and Computing Graphs ［C］／／Proceedings of ICF International Symposium on Fracture Mechanics.Beijing：Science Press，1983，300－306.

［11］ 赵晋芳，谢里阳，刘建中，等.有限板共线多孔 MSD应力强度因子有限元分析［J］.组合机床与自动化加工技术，2009（1）：4－7.

［12］ 赵海涛，战宝玉，杨永腾.基于ANSYS的应力强度因子计算［J］.煤矿机械，2007，28（2）：22－23.