在机检测中基于CVT结构的可展曲面采样策略

郑惠江 王太勇 何改云

天津大学，天津，300072

0 引言

在机检测系统是在加工中心原功能的基础上增加了产品质量检测的功能，建立起无需脱离生产环境即可完成加工—检验—再加工的闭环制造系统。在该系统中，根据CAD模型数据，按照采样策略进行采样点的选择和布局后，进行测量轨迹的规划，是在机检测系统实现其基本功能的重要基础之一。

在机检测过程是采用接触式测头从工件表面点集的总体中选择若干样本来对总体情况进行评估的一种离散采样过程。其中，采样点的规模直接影响到检测过程花费的时间，离散采样的误差直接影响到检测质量［1］。因此，如何选择样本，使其既能准确地反映总体情况，又能减少采集的数据量，从而降低生产成本［2］是在机检测必须要考虑的重要因素之一，也是判别采样策略好坏的重要标准。

常用的采样方法有均匀采样法、随机采样法、Hammersley序列采样法和Halton序列采样法等。均匀采样法［3－5］只有当采样数量足够多时，才能较好地反映采样面的情况，但所需采样时间过长；而当采样点数量较少时，会造成测量结果与实际结果相差很远，不具备参考性［6－8］。随机采样法由于采用纯粹偶然的方法从总体中选取样本，使得测量过程标准不一［7］。随后发展的拉丁超立方体抽样（latin hypercube sampling，LHS）方法所获得总均值的方差比简单随机抽样的方差要小［9］。其后提出的 Hammersley序列采样法和Halton序列采样法可以有效地降低采样密度，并且能保证测量精度［1－3，10］。另外，董玉德等［7］在深入分析了Halton采样法的基础上，针对具体的几何体给出相应的采样算法，并验证了Halton序列采样策略比随机采样策略具有更均匀的采样点分布。

本文利用CVT（centroidal voronoi tessellation）结构的特性，提出了基于CVT结构的可展面采样策略。

1 基于CVT结构的可展面采样策略

1.1 CVT结构采样方法

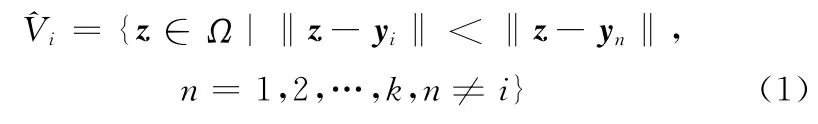
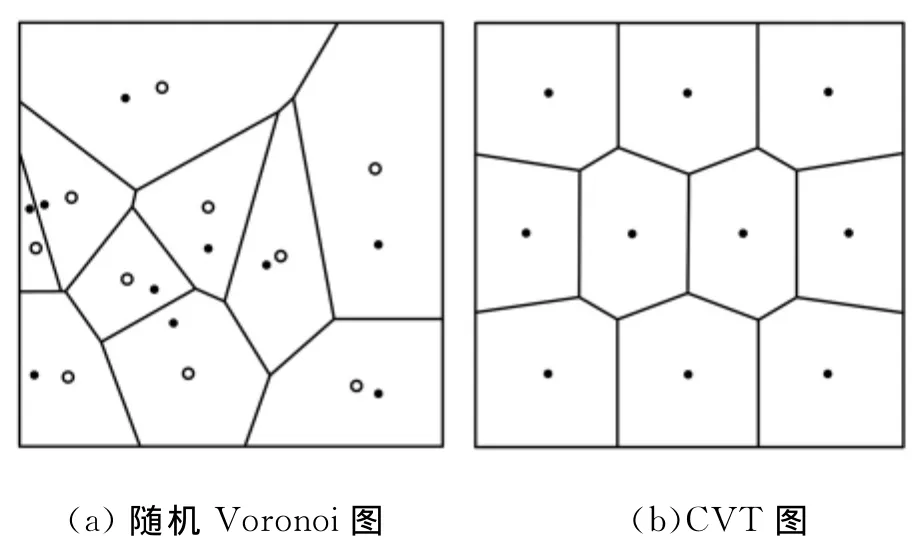
图1 随机Voronoi图和CVT图

CVT是Voronoi结构的一种特殊形式，具有很多良好的特性，在图像压缩、聚类分析和数值积分优化等领域中得到广泛应用［11－12］。CVT结构采样法就是在在机检测（或其他坐标检测）的过程中，选择适当的密度函数ρ（y），将检测区域Ω按照上述方法进行细分后，再以为采样点对其进行采样。

1.2 可展面采样策略

Hammersley序列和Halton序列特别适合矩形平面，对于如圆、圆锥等其他几何体必须进行相应的变形才可以计算出各种几何体的采样点分布情况［8］。

CVT采样方法不仅适用于矩形平面的采样，而且对于平面采样的形状没有具体的要求，适用于多种平面形状区域的采样（图2）［13，15］，因此其使用范围十分广泛。

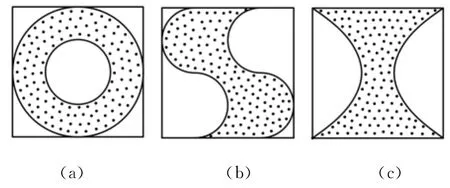
图2 几种不同平面区域中采用CVT法采样点布局结果

根据经典微分几何，对于给定的参数曲面S（u，v），可以定义其Gauss曲率为

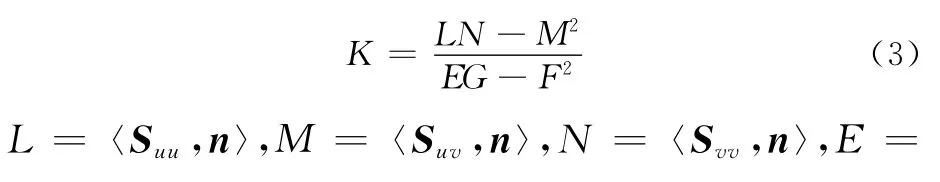
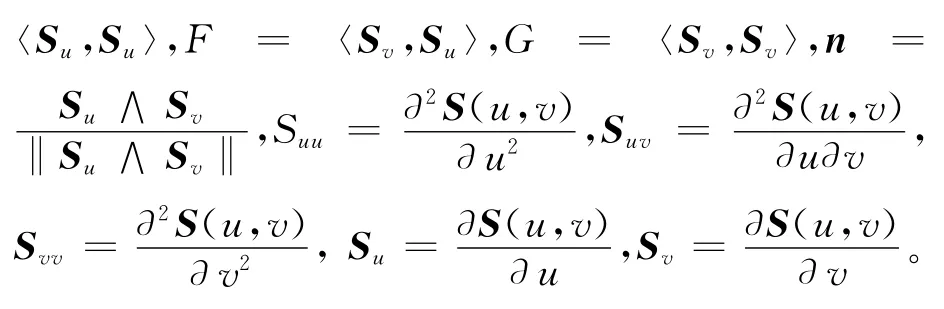
当K＝0时，称该曲面为可展曲面，可展曲面是一种特殊的直纹曲面。在飞机、船体、汽车、风力发电机叶片等重大装备的设计和制造等工程应用中，可展曲面是一类非常重要的曲面。因此，其加工质量的检验及采样点布局策略也是制造业中研究的一个重要内容。

由于可展曲面可以严格展开成平面，则存在映射f：R3→ R2，使 得（x，y）＝f（x′，y′，z′）成立，其中（x′，y′，z′）表示可展曲面上的任意一点坐标，（x，y）表示其展开到平面坐标系下的坐标。显然，同时存在映射f－1：R2→ R3，使得（x′，y′，z′）＝f－1（x，y）成立。利用以上两个映射，可采用图3所示的采样策略选取可展曲面的采样点集。

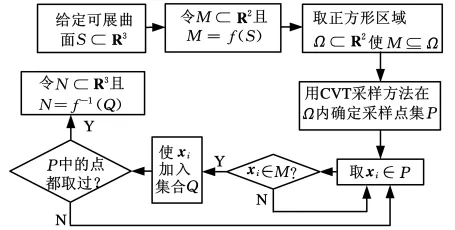
图3 可展曲面CVT采样策略流程图

1.3 计算实例

以圆柱面为实例，将圆柱面按图3所示的算法过程展成平面，在该平面内按照基于CVT结构的采样策略进行采样点分布。这里采用直角坐标系表示圆柱面上的点坐标，则映射f和f－1由式（4）和式（5）分别来定义：

式中，（x，y，z）为圆柱表面的直角坐标；（x′，y′）为展开的平面坐标

若采样点分布在300×300的平面上，采样点数N 分别为16、64、169和256，使用MATLAB6.5按照上述可展曲面CVT采样策略对计算实例进行运算，得到的圆柱面的采样点分布结果如图4所示。

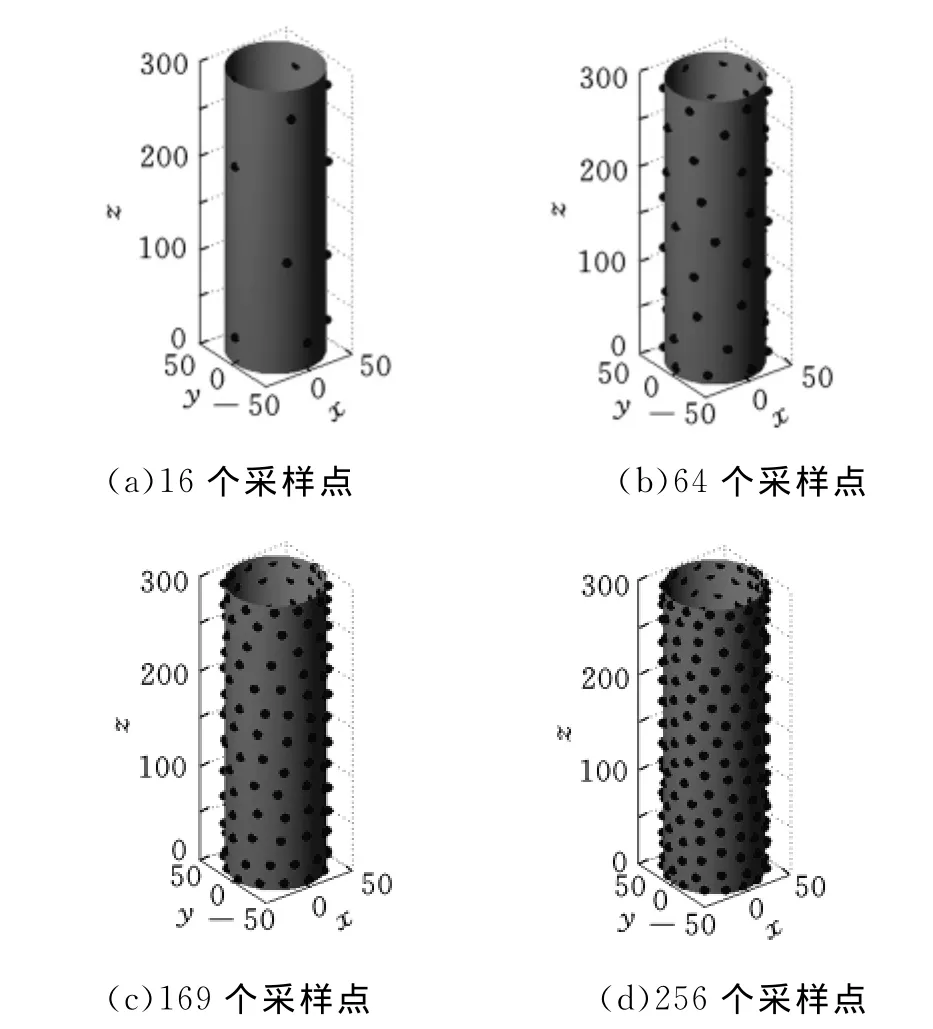
图4 基于CVT结构采样策略的采样点布局

2 采样策略对检测结果的影响分析

考虑到随机过程可很好提供加工表面一阶、二阶以及更高阶的统计量的情况，可通过构建相应的随机过程来对不同粗糙度的加工表面进行数值模拟仿真［1，10-11］。

本文采用各向同性随机过程来模拟加工表面：

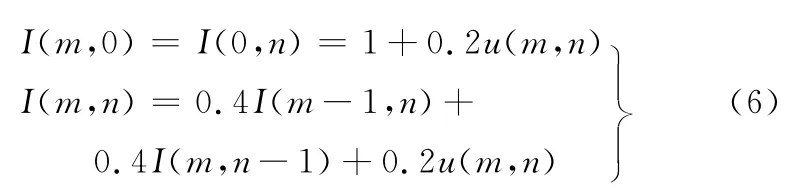
其中，u（m，n）～N（0，1），该表面又可称为高斯表面［10］，其数值模拟实例如图5所示。

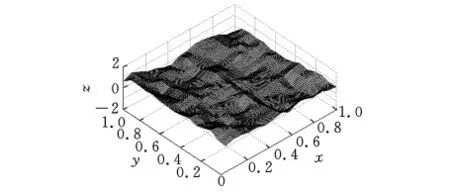
图5 高斯表面实例

分别采用Hammersley序列采样法、Halton序列采样法和基于CVT结构的采样方法进行采样，对采样点的分布进行对比。采样点同样分布在300×300的平面上，采样点数N仍分别为16、64、169和256，各种采样点的分布结果如图6～图9所示。然后分别计算不同采样点数下各种采样方法采样点的采样误差均值和标准偏差值，3种采样方法对检测结果影响的具体情况如表1所示。

图6 不同采样方法16个采样点布局比较

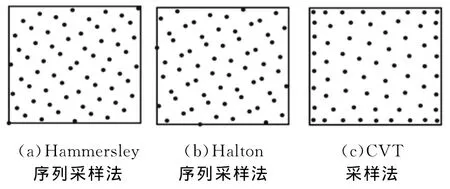
图7 不同采样方法64个采样点布局比较

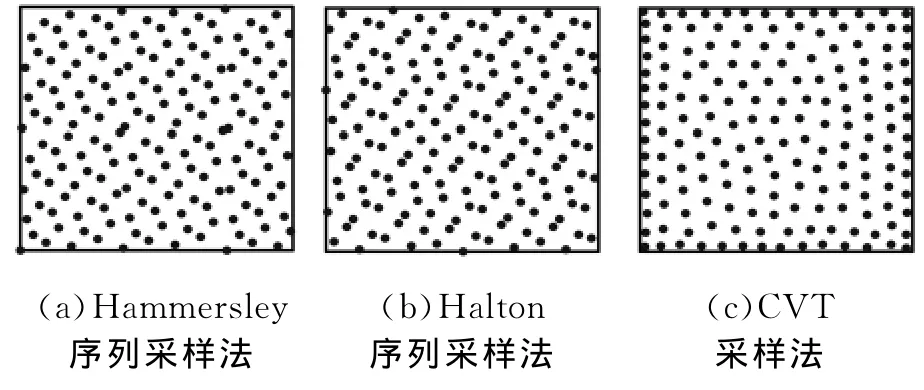
图8 不同采样方法169个采样点布局比较

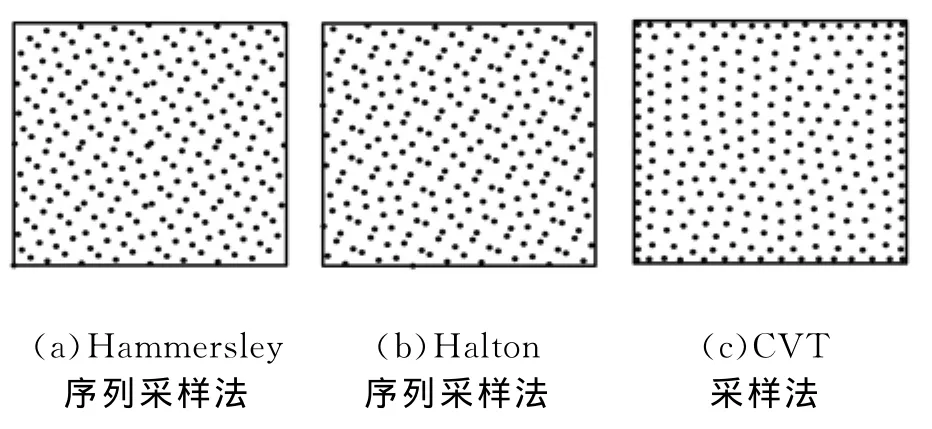
图9 不同采样方法256个采样点布局比较

表1 不同采样方法的采样点误差均值与标准偏差值

从表1的数据中可以看出，在不同的采样点数目下，CVT采样方法的采样点误差的值均小于Hammersley序列采样法和Halton序列采样法，其总体的平均值比其他两种采样方法分别小约19.3%和28.5%，其总体的标准偏差值也分别降低约67.1%和78.9%，表明其采样过程中的采样结果稳定性更好。另外，CVT采样方法整体采样结果＾μr值的标准偏差比其他两种采样方法分别降低了约86%和83.1%。说明在加工表面存在粗糙度的采样过程中，CVT采样方法表现出更为准确的采样精度和更为稳定的采样结果。因此，在同样采样精度的要求下，CVT采样方法可以有效降低采样点的数量，从而有效提高采样效率。

3 采样策略对采样点分布均匀性的影响分析

文献［7］和文献［11］提出用采样点在采样面上的分布均匀性来评价采样策略的优劣。而采样点均匀性可以从三个方面来描述：①在采样空间中，采样点与其他采样点是否相近；②采样点的密度均匀性是否能够覆盖整个采样空间；③采样点布局是否具有各向同性。为此分别定义变量dis和dev来考察Hammersley序列采样法、Halton序列采样法和基于CVT结构的采样方法的采样点分布的均匀性情况。

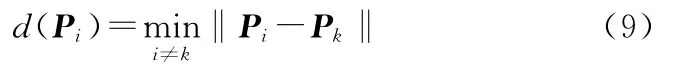
可以给出如下两个定义：

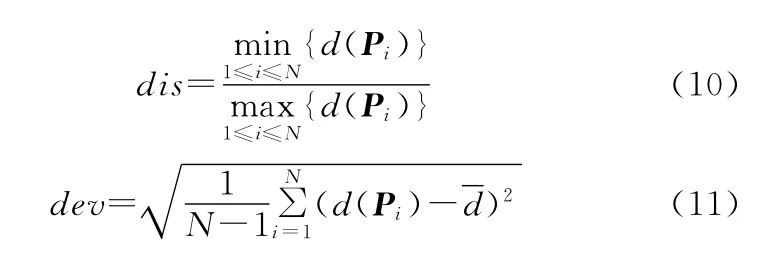
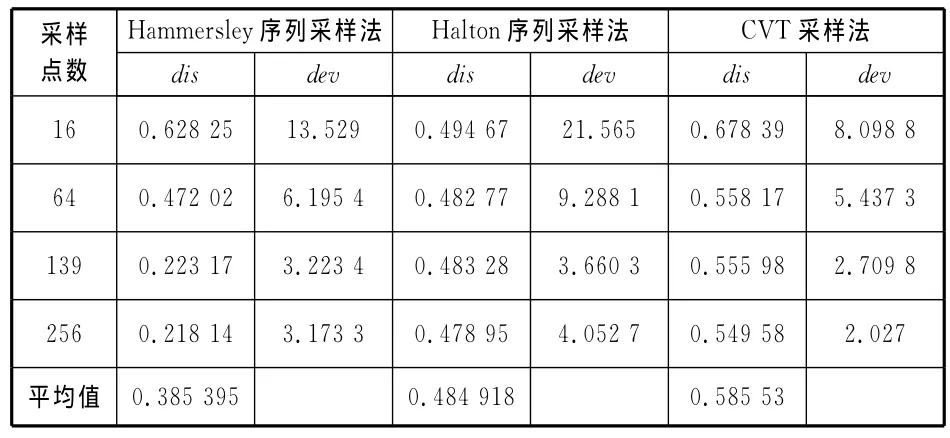
表2 不同采样方法的采样点分布均匀度比较

从图6～图9中可直观看出，CVT采样方法相对于Hammersley序列采样法和Halton序列采样法有着较为均匀的采样点分布。而且，随着采样点数的增加，CVT采样法的采样点分布均匀性更好。表2的数据中也很好地证明了这一点，在4种不同采样点数下，CVT采样法的dis值均大于其他两种采样方法dis值，其平均值分别比Hammersley序列采样法和Halton序列采样法高出近52%和21%；同时，在相同采样点数下，CVT采样法的采样点间最小距离的标准偏差值dev比其他两种采样方法都小，平均要小35.53%，其中最大值为62.44%，表明CVT算法可以较大幅度地提高采样点的分布均匀性。

4 结束语

本文讨论了在机检测测量过程中的采样问题，对常用的采样方法和策略进行了分析，给出了基于CVT结构的采样方法。利用可展曲面的空间坐标映射关系，提出了基于CVT结构的可展曲面采样取点策略。将各种采样策略的采样结果进行了对比，对比结果表明基于CVT结构的采样策略比其他采样方法具有更好的稳定性、均匀性和更准确的采样精度。该方法同样可应用于各种可展曲面的采样过程中。

［1］ Woo T C，Liang R，Hsieh C C，et al.Efficient Sampling for Surface Measurements［J］.Journal of Manufacturing Systems，1995，14（5）：345－354.

［2］ Lee G，Mou J，Shen Y.Sampling Strategy Design for Dimensional Measurement of Geometric Features U－sing Coordinate Measuring Machine［J］.International Journal of Machine Tools ＆ Manufacture，1997，37（7）：917－934.

［3］ Kim W S，Raman S.On the Selection of Flatness Measurement Points in Coordinate Measuring Machine Inspection［J］.International Journal of Machine Tools and Manufacture，2000，40（3）：427－443.

［4］ Saito K，Miyoshi T，Yoshikawa H.Noncontact 3－D Digitizing and Machining System for Free－form Surface［J］.Annals of the CIRP，1991，40（1）：483－486.

［5］ Smith K B，Zheng Y F.Multi－laser Displacement Sensor Used in Accurate Digitizing Technique［J］.Transactions of the ASME，Journal of Engineering for Industry，1990，16（11）：482－490.

［6］ Raghunandan R，Venkateswara Rao P.Selection of an Optimum Sample Size for Flatness Error Estimation while Using Coordinate Measuring Machine［J］.International Journal of Machine Tools ＆ Manufacture，2007，47（3）：477－482.

［7］ 董玉德，汪玉玺，刘达新，等.三角平面Halton点采样策略及其性能分析［J］.计算机辅助设计与图形学学报，2007，19（8）：1063－1068.

［8］ Raghunandan R，Venkateswara Rao P.Selection of Sampling Points For Accurate Evaluation of Flatness Error Using Coordinate Measuring Machine［J］.Journal of Materials Processing Technology，2008，202（1／3）：240－245.

［9］ 方开泰.均匀试验设计的理论、方法和应用——历史回顾［J］.数理统计与管理，2004，23（3）：69－80.

［10］ Woo T C，Liang R.Dimensional Measurement of Surfaces and Their Sampling［J］.Computer－aided Design，1993，25（4）：233－239.

［11］ Romero V J，Burkardt J S，Gunzburger M D，et al.Initial Evaluation of Centroidal Voronoi Tessellation Method for Statistical Sampling and Function Integration［C］／／The 4th International Symposium on Uncertainty Modeling and Analysis（ISUMA’03）.Washington DC：IEEE Computer Society，2003：174－191.

［12］ Romero V J，Burkardt J S，Gunzburger M D，et al.Initial Application and Evaluation of a Promising New Sampling Method for Response Surface Generation：Centroidal Voronoi Tessellation［C］／／AIAA／ASME／ASCE／AHS／ASC. The 44th Structures，Structural Dynamics，and Materials Conference（5th AIAA Non－Deterministic Approaches Forum）.VA：American Inst.Aeronautics and Astronautics Inc.，2003：5527－5542.

［13］ Qiang Du，Gunzburger M，Ju Lili.Meshfree，Probabilistic Determination of Point Sets and Support Regions for Meshless Computing［J］.Comput.Meth.Appl.Mech.Engrg.，2002，191（13／14）：1349－1366.

［14］ Qiang Du，Faber V，Gunzburger M.Centroidal Voronoi Tessellation：Applications and Algorithms［J］.SIAM Review，1999，41（4）：637－676.

［15］ Ju Lili.Probabilistic and Parallel Algorithms for Centroidal Voronoi Tessellations with Application to Meshless Computing and Numerical Analysis［D］.Iowa：Iowa State University，2002.