GO法在产品装配过程质量分析中的应用研究

张根保 葛红玉

重庆大学，重庆，400044

0 引言

装配是产品生产活动中花费成本最高，对质量影响最大的一个环节，据统计，在产品生产阶段，有1／3以上的人直接或间接从事与装配有关的活动，对于飞机、船舶等复杂产品，这个比例会更高［1］。因此，确保产品装配过程质量是提高产品质量的有效手段。复杂产品的装配与严格的工艺要求有关，装配过程是一个流程，装配线应以不中断为约束［2］，装配工艺中每道工序中的任何一道工步出现异常都会影响装配质量。为了保证装配质量，进行装配质量的分析评价就变得尤为重要。

统计过程控制（SPC）是普遍采用的一种实时在线质量监测技术［3］，控制图可对生产过程中的质量异常实现报警。决策树［4］、专家系统［5］、人工神经网络［6］等被用于制造过程质量的诊断和控制，Bayesian和Dempster－Shafer理论被用于多品种、小批量生产的质量诊断和控制。对于装配过程这种有多重状态、有时序功能变化的系统来讲，上述方法在解决问题的时候就会变得更为复杂。

本文试图应用GO法这种全新概念的系统可靠性分析方法，对产品装配过程质量进行分析，该方法的应用可以避免分析装配过程的复杂性。应用GO法对产品装配过程进行分析的目标就是由装配过程单元的状态来确定整个装配过程的正常状态概率。本文以齿轮油泵装配过程为例，对GO法在装配过程中的应用进行了阐述。

1 GO法概述

GO法是一种以成功为导向的系统可靠性分析技术［7－8］，是系统可靠性或逻辑关系的分析方法，其基本思想是把系统原理图、流程图或工程图直接按一定规则“翻译”成GO图，再通过GO图对系统进行定性和定量分析。GO法是通过建立GO图和进行GO运算来实现的。它的分析过程是从输入事件开始，经过对GO法模型的计算确定系统的正常概率。GO法的核心步骤就是建立GO图和进行GO运算，GO图和GO运算的两大要素就是操作符和信号流，GO法中用操作符代表单元功能和特征，操作符的属性有类型、数据和运算规则，类型是操作符的主要属性，GO法定义了17种标准的操作符，以类型1～17表示（见文献［9］）。GO法中信号流表示系统单元的输入和输出以及单元之间的关联，信号流连接GO操作符生成GO图，信号流的属性是状态值和状态概率。GO法用于系统可靠性分析的具体过程如图1所示［10－12］。

图1 GO法分析流程图

图1中，定义系统即确定分析对象的范围、功能和部件，给出原理图、工程图或流程图；成功准则即明确什么是系统的正常运行状态或过程的正常状态；输入数据即确定各单元的状态概率然后按操作符编号输入数据。

2 产品装配过程的一般框架

任何产品都是由许多零件和部件组成的［13］。由于产品的复杂程度不同，故零件或部件的组合情况也不同。在复杂产品的装配过程中，零件数量多，结构复杂，精度要求高，相互之间存在协调关系。产品的装配过程就是由零件组装成组件、再由组件组装成部件、由部件组装成总成和最后组装成产品的过程。这些零件、组件、部件又是按照多道工步装配成产品的。具体产品不同，其装配过程也不同，现建立包括零件、组件、部件等较完整的多道工步装配过程的一般框架，如图2所示。

图2表达了有时序的装配过程，整个装配过程由主装配线、装配线1及装配线2组成，装配线1与装配线2代表部件的装配单元，图中方框表示装配单元中每道工步。由图2可看出，在装配过程中如果有一道工步出现异常，就会影响整个装配过程的质量，那么根据各道工步的正常概率可以判断出装配质量的正常概率。

3 齿轮油泵装配过程质量的GO法分析

3.1 齿轮油泵装配过程系统分析

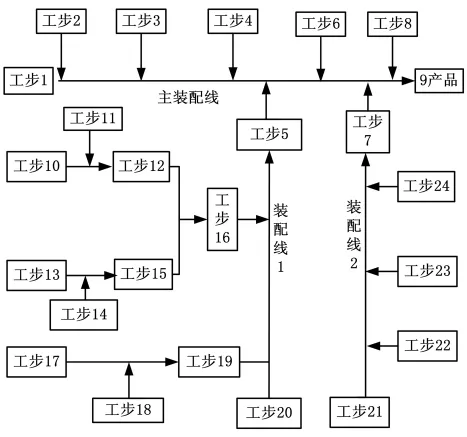
图2 产品装配过程一般框架

以齿轮油泵装配过程质量分析的GO法应用为例，阐述GO法在装配过程质量分析中的具体步骤。齿轮油泵装配过程由4个装配单元组成，分别为主动齿轮组的安装、从动齿轮组的安装、泵体组件的安装，以及最后按顺序装入安全阀。第1个单元由1道工步组成，第2个单元由3道工步组成，第3个单元由10道工步组成，第4个单元由1道工步组成。根据第2节中产品装配过程一般框架的建立过程，建立齿轮油泵装配过程框架图，如图3所示。

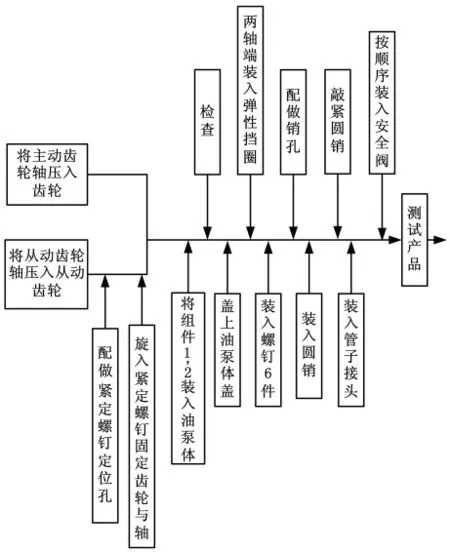
图3 齿轮油泵装配过程框架

3.2 建立GO图

将齿轮油泵装配过程中的多道工步用操作符表示，各道工步之间的连接用信号流表示。每个装配层上的第1道工步用类型5的输入操作符表示，单输入单输出的零部组件用类型1两状态操作符表示，多输入单输出部组件用类型10的与门操作符表示，这些操作符中的S表示输入信号，R表示输出信号，每个操作符的输入信号是上一个操作符的输出信号。操作符代表的各道工步都有正常和异常两个状态。整个装配过程以第1道工步为始端，最后一道工步为终端，整个过程只有正向导向，没有反馈。操作符中横杠后面的数字为工步序号。

齿轮油泵装配过程中有16个操作符和16个信号流，主动齿轮组与从动齿轮组中的各道工步是两状态类型，因此用两状态操作符表示，主动齿轮组和从动齿轮组与油泵体进行装配时，若两者都正常，则这两道工步才处于正常状态，因此用与门操作符表示输出的逻辑关系。从第6道工步到最后一道工步都是两状态类型，因此用两状态操作符表示各道工步。建立了齿轮油泵装配过程GO图（图4）。

图4 齿轮油泵装配过程GO图

3.3 输入数据

齿轮油泵装配过程各道工步的状态概率值见表1。根据装配顺序将各装配单元按序号列出，每个单元中的工步序号与图4中的操作符编号对应，状态值0表示该工步正常，状态值1表示该工步异常。工步的正常概率是根据装配多次的各道工步正常次数与总装配次数之比得来的。

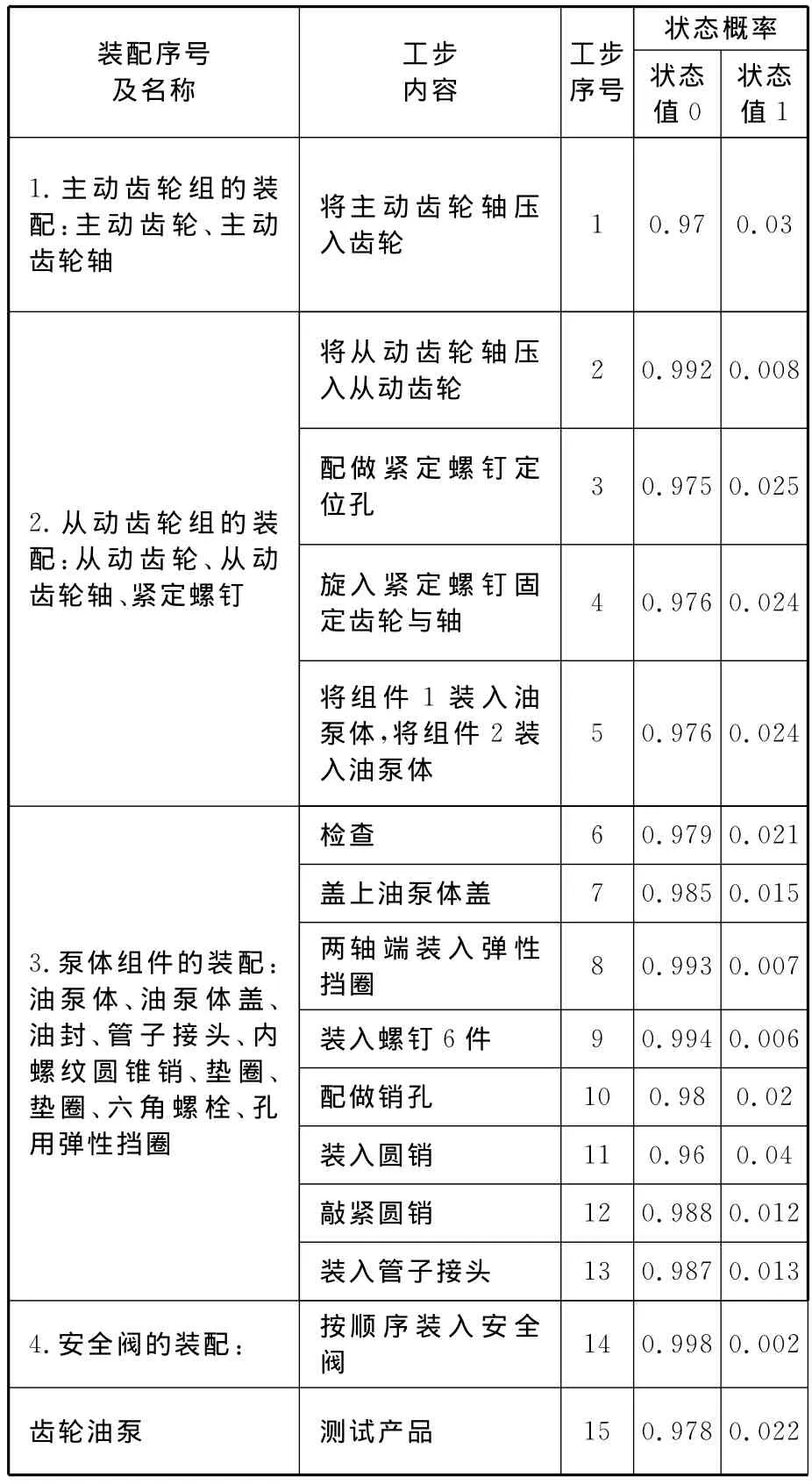
表1 装配工步的正常异常概率值

3.4 齿轮油泵装配过程质量正常概率的GO法运算

齿轮油泵装配过程中用到3种操作符，分别为类型1、类型5、类型10操作符。根据操作符代表的各道工步特性确定操作符的状态概率，从输入操作符开始，操作符逐个按运算规则，由操作符输入信号状态和操作符的状态概率组合积累规律进行运算，得到输出信号的状态概率与输入信号状态和操作符状态概率的关系，那么，当知道输入信号状态概率和操作符状态概率的初始值时，就可以计算整个装配过程的输出状态概率值。

为研究问题的方便，需对基于GO法的运算条件进行假设：现设PRi（0）为操作符输出信号正常状态概率，PRi（1）为操作符输出信号异常状态概率；PCi（0）为操作符的正常状态概率，PCi（1）为操作符的异常状态概率；PSi（0）为类型1、类型10操作符输人信号正常状态概率，PSi（1）为类型1、类型10操作符输入信号异常状态概率。其中，i为工步序号即三角形或圆形中横杠后面的数字。

采用概率公式算法，沿信号流方向，由操作符概率计算公式直接定量计算齿轮油泵装配过程质量的正常状态概率。现给出关键信号流和最终信号流的表达式。

（1）信号流4：

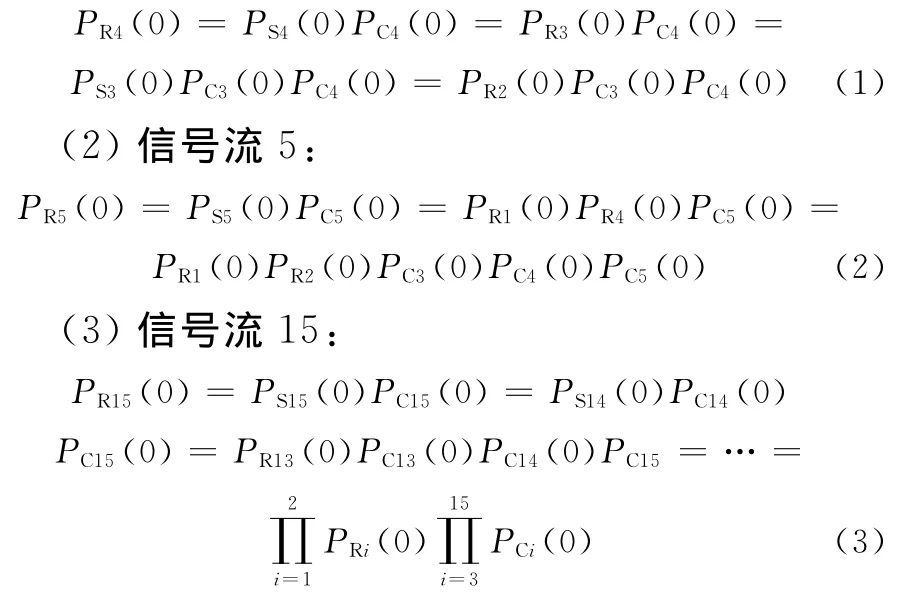
由于装配过程中有一道工步出现异常就会导致整个装配质量的异常，当有两道及两道以上工步出现异常时，装配质量肯定是异常的，且引起装配质量异常的状态组合繁多，直接计算异常概率就会产生“组合爆炸”现象，因此应先求出装配质量的正常概率，然后根据装配质量正常概率与异常概率之和为1，再求出其异常概率。齿轮油泵装配质量正常概率与异常概率的关系式为

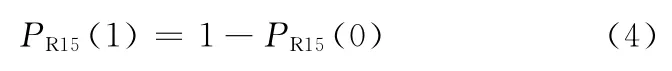
当已知装配过程中各道工步的正常概率时，便可由式（3）求出装配总输出质量的正常概率，然后根据式（4）求出装配质量异常状态的概率。

将表1中数据代入上述公式可得

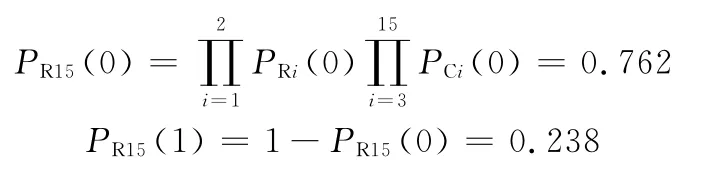
由结果可以判断出齿轮油泵装配过程输出质量的正常概率为0.762，异常概率为0.238，整个系统装配质量有待提高23.8个百分点。

4 结束语

本文基于产品装配过程，将GO法引入到产品装配过程质量的分析中，以齿轮油泵装配过程为例，探讨了GO法在产品装配过程质量正常概率计算中的应用。由以上分析可以看出，GO法思路简单清晰，在装配过程质量分析的应用中，可以进行正常概率的直接计算。

由于装配在产品制造过程中占很大的比重，因此分析产品装配过程质量对于质量的提高尤为重要，GO法的应用为装配过程质量的分析提供了新的思路。

［1］ 赵罡，王超，侯文君，等.复杂产品虚拟装配系统的人机交互技术［J］.北京航空航天大学学报，2009，35（2）：138－141.

［2］ 陈宗舜，刘方荣，吴春燕，等.机械制造装配工艺设计与装配CAPP［M］.北京：机械工业出版社，2006.

［3］ 王毓芳，肖诗唐.统计过程控制的策划与实施［M］.北京：中国经济出版社，2004.

［4］ Ruey－Shun C，Kun－Chieh Y.Using Data Mining Technology to Improve Manufacturing Quality：A Case Study of LCD Driver IC Packaging Industry［C］／／Proceedings of the Seventh ACIS International Conference on Software Engineering.Artificial Intelligence，Networking，and Parallel／Distributed Computing（SNPD 2006）.Washington DC：IEEE Computer Society，2006：115－119.

［5］ Landryova L，Irgens C.Process Knowledge Generation and Knowledge Management to Support Product Quality in the Process Industry by Supervisory Control and Data Acquisition Open Systems［J］.Production Planning ＆ Control，2006，17（2）：94－98.

［6］ 乐清洪，腾霖，朱名铨，等，质量控制图在线智能诊断分析系统［J］.计算机集成制造系统－CIMS，2004，10（12）：1583－1587.

［7］ 王淑娟，王桂丽，霍国富.GO法在铁路客车电子防滑器仿真综合试验系统可靠性分析中的应用研究［J］.系统工程理论与实践，2006，26（10）：95－101.

［8］ 沈祖培，唐辉.有共因失效的系统可靠性的GO法分析［J］.清华大学学报（自然科学版），2006，46（6）：829－832.

［9］ 沈祖培，黄祥瑞.GO法原理及应用—— 一种系统可靠性分析方法［M］.北京：清华大学出版社，2004.

［10］ 刘双杰.GO法及在机电系统可靠性分析中的应用［J］.黑龙江科技信息，2009，（3）：55－57.

［11］ 高振清，孙厚芳，吴琼.基于GO法的制造系统可靠性分析［J］.机械科学与技术，2007，26（3）：320－323.

［12］ Shen Z P，Gao J，Huang X R.A New Qualification Algorithm for the GO Methodology［J］.Reliability Engineering and System Safety，2000，67：241－247.

［13］ 徐旭松，杨将新，曹衍龙，等.一种面向可装配性的公差分析方法［J］.中国机械工程，2008，19（24）：2976－2981.