非正弦振动结晶器内保护渣道动态压力变化规律
王宏明,宋邦民,李桂荣,赵玉涛
(江苏大学 材料科学与工程学院,江苏 镇江,212013)
连铸结晶器非正弦振动能在高拉速下保证结晶器振动的平稳性,有效减小铸坯表面振痕和控制皮下夹渣等缺陷,并有利于增加保护渣流量,从而使润滑效果提高,减少漏钢事故率,是发展高效连铸的关键技术[1],因此,选择与拉坯速度相匹配的结晶器振动参数对提高铸坯质量和连铸效率都具有重要意义[2]。由于结晶器振动使保护渣道压力呈周期性变化,且正是该周期性变化的渣道压力对连铸坯质量、拉坯阻力、渣流量、撕裂坯壳的愈合等起决定性影响[3],因此,必须优化振动参数以将保护渣道压力控制在合理范围,使保护渣既能起到好的润滑效果,减小拉坯阻力,防止坯壳裂纹和拉坯漏钢,又能保证脱模和最大限度地减轻振痕[4-5]。由于保护渣道宽度在10-2~10-1mm数量级,难以直接进行精确测量[6],Kajitani等[7-8]建立了忽略结晶器振动的渣道压力计算模型,研究了渣流量和黏度对渣道压力的影响;Lei等[9]建立模型研究了磁场对渣道压力的影响,但同样没有考虑结晶器振动条件。本文作者结合结晶器非正弦振动规律和保护渣润滑理论,建立了保护渣道压力计算模型,研究结晶器非正弦振动参数及拉坯速度对渣道动态压力的影响,以便为优化结晶器非正弦振动技术提供参考。
1 结晶器非正弦振动速度规律确定
图1所示是结晶器振动速度和位移变化曲线。振动速度曲线由水平段bc、抛物线段cd、余弦段deg、抛物线段gj、水平段jl光滑连接组成。结晶器振动速度vm的表达式为[10]:
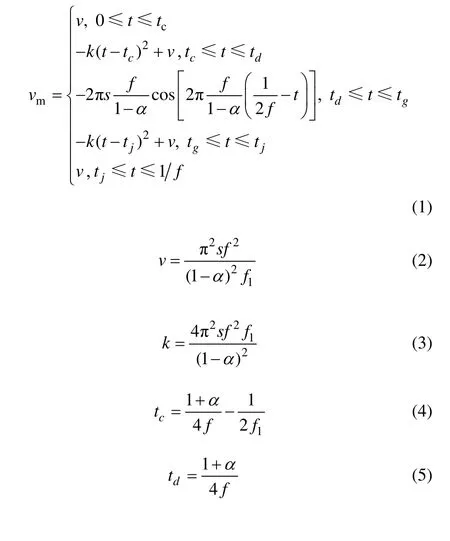
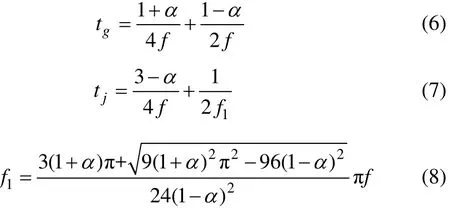
式中:v为最大上振速度,m/min;k为系数;s为振幅,m;f为振频,min-1;t为时间,min;α为非正弦因子,α=4tmf;tm为非正弦振动最大位移滞后时间,min;f1为抛物线速度段频率,min-1;tc,td,tg,tj分别为振动速度曲线中c,d,g,j点时间,s。从式(1)~(8)可知:非正弦振动波形由α,f和s 3个独立变量确定。

图1 结晶器振动速度曲线和位移曲线Fig.1 Curves of mold oscillation speed and position
2 保护渣道动态压力计算模型
图2所示是保护渣道示意图。保护渣流入由结晶器和凝固壳构成长度为 lf、入口宽度 hi、出口宽度 hf的保护渣道。

图2 保护渣道模型示意图Fig.2 Schematic diagram of flux channel model
2.1 控制方程
保护渣道内渣流动的动量方程为[11]:

式中:p为保护渣道内压力,Pa;μf为保护渣黏度,Pa·s;ρf为保护渣密度,kg/m³。
保护渣相对流量QR满足连续性方程:
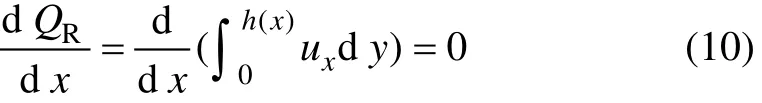
式中:ux为保护渣相对流速,ux=vf-vs;νf和νs分别为保护渣流速和拉坯速度,m/s;h(x)为渣道形状函数。
2.2 边界条件确定与求解
结晶器壁面 (y=0,0<x<lf): ux=vm-vs;
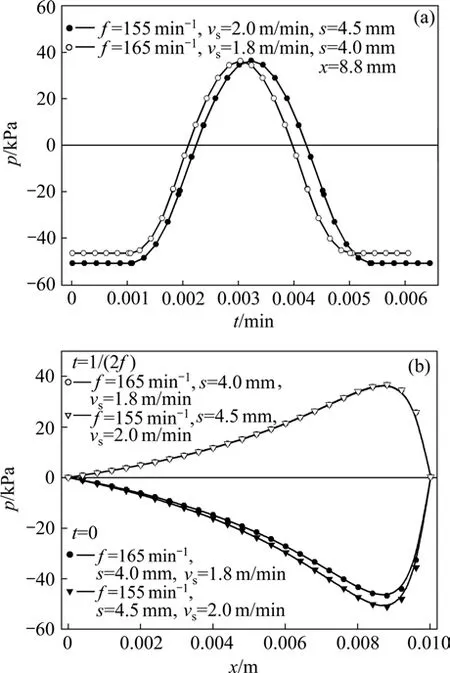
凝固坯壳壁面 (y=h(x),0 渣道入口 (x=0,0≤y≤hi): p=pi; 渣道出口 (x= lf,0≤y≤hi): p=pf。 联立式(9)和(10),积分后代入边界条件可推导出保护渣道压力计算方程为: 根据国内某钢厂板坯连铸机工艺条件,确定计算基本参数见表1。研究非正弦振动参数非正弦因子α、振幅s、振频f以及拉坯速度vs对保护渣道动态压力的影响。 图3所示是α在0~0.396范围内变化对结晶器振动速度的变化。从图3可见:随着α增加,结晶器最大上振速度减小,上振过程平缓,正滑脱相对速度差减小,而且由于正滑动时间延长,可有效增加保护渣消耗量,提高润滑效果,所以,α增加可以保证高速连铸时的结晶器振动的稳定性和润滑,显著降低结晶器壁与坯壳间的最大摩擦力,减小最大拉坯阻力以控制初凝坯壳裂纹和拉漏[12-13];同时,负滑脱时间缩短,最大负滑脱速度增加,在较短的负滑脱期内产生更高的负滑脱量,对初凝壳施加压应力达到强制脱模和使裂纹愈合的目的,解决了高速连铸脱模困难的问题,而且负滑脱期短,可以提高铸坯表面质量。这是高速连铸采用非正弦振动的优势之一。 图4所示是不同α时保护渣道压力随高度和时间的变化。由图4可知:结晶器振动负滑脱期渣道内最大正压力随着α增加而增加,且增加幅度随α增加而增大;正滑脱期内渣道最大负压随α增加而减小,其减小的幅度也随着α增加而减小。振动负滑脱期渣道正压力的作用是强制坯壳脱模、愈合撕裂的坯壳,防止拉坯漏钢,但正压过大则易导致铸坯表面振痕加深、表面夹渣等缺陷,降低铸坯质量;振动正滑脱期渣道负压力的作用是增加保护渣流量,提高润滑效果,降低拉坯阻力[11]。α增加使负压减小,但使渣道呈负压状态的时间延长,所以,α从0增加到一定值时,渣流量增加。α的选择应使渣道内正负压力波动控制在合适的范围,同时延长正滑脱时间以增加渣流量,并缩短负滑脱时间以提高铸坯表面质量。因此,在该拉速及振幅振频参数下,α的最佳值约为0.2[14],此时,渣道正负压都在合理范围内,且最大正负压差最小。 表1 基本计算参数Table 1 Main parameters in calculation model 图3 不同α时结晶器振动速度的变化Fig.3 Variations of mold oscillation speed at different non-sinusoidal factors 图4 不同α时保护渣道压力随高度和时间的变化Fig.4 Variations of pressure of flux channel with height and with time at different non-sinusoidal factors 图5 所示是振幅s变化对渣道压力变化规律的影响。由图5可知:随着振幅增加,保护渣道内正滑脱期的最大负压和负滑脱期的最大正压都增加,在1个振动周期内,渣道动态压力的波动范围增加,有利于铸坯的脱模、愈合撕裂的坯壳和增加保护渣流量,提高润滑效果,减少拉坯漏钢事故。但动态压力波动增加,不利于金属弯月面的稳定并影响铸坯表面质量,所以,在保证脱模和润滑的前提下,应尽量采用小振幅振动。此外,振幅增加使渣道最大正压增加的幅度明显高于负压的增加幅度,说明振幅对最大正压有更重要影响;因此,当铸坯表面振痕较深时,应适当降低振幅,同样,当发生脱模困难时,增加振幅是一种有效措施,但要考虑振幅增加对铸坯表面质量产生的不利影响。 图5 振幅变化对保护渣道压力的影响Fig.5 Effects of stroke of mold oscillation on pressure of flux channel 图6 所示是振频f变化对渣道压力的影响。由图6可知:振频增加使保护渣道内负滑脱期的最大正压明显增加,但正滑脱期的最大负压增加很小,这说明增加振频对强制脱模、愈合拉裂的坯壳有重要作用,但正压过大也对铸坯表面质量有不利影响。因此,对于高速连铸机结晶器,采用高频小振幅振动[15]可以有效脱模、防止拉裂和漏钢事故,但振频不宜过高。因为振频增加使渣道正压明显增加,对负压影响很小,不利于增加渣流量,使润滑效果差而影响铸坯表面质量,因此,应根据渣道压差控制振频在合理范围内。 图6 振频变化对保护渣道压力的影响Fig.6 Effects of frequency of mold oscillation on pressure of flux channel 图7 所示是拉坯速度变化对渣道压力的影响。由图7可知:拉坯速度增加,振动负滑脱期的最大正压减小,而振动正滑脱期的最大负压增加。因此,增加拉速可以增加保护渣的流量,但正压减小不利于铸坯脱模和拉裂坯壳的愈合。故拉速提高时,应适当增加振幅以增加负滑脱时的正压,保证脱模和防止拉漏事故,同时,可以增加正滑脱期的负压以增加保护渣流量,提高润滑效果,减少拉坯阻力,从而提高铸坯质量。 图7 拉坯速度变化对保护渣道压力的影响Fig.7 Effects of casting speed on pressure of flux channel 根据以上分析,对国内某钢厂SPHC钢板坯连铸机振动方式进行了优化,图8所示为实际优化工艺参数条件下保护渣道压力的比较结果。由图8可知:拉坯速度由1.8 m/min提高到2.0 m/min,通过增加振幅(4.0~4.5 mm)和降低振频(165~155 min-1),使保护渣道正压基本相等,产生的负滑脱起到强制脱模和愈合撕裂坯壳的作用;拉速提高时,渣道的负压适当增加,以增加保护渣流量,提高润滑效果。在实际生产中,当连铸机采用上述2种工艺参数时,铸坯的表面质量较采用正弦振动时有明显提高,振痕平均深度减小50%以上,完全消除了振痕波谷处的微裂纹,并有效 控制了板坯表面夹渣现象,同时,保护渣消耗量增加25%左右,明显提高了润滑效果,尚未发生拉坯漏钢事故。这说明上述2种拉速下的振动参数合理可靠,也说明本模型及分析的合理性和可靠性。 图8 实际优化工艺参数下保护渣道压力的比较Fig.8 Comparisions of pressure of flux channel at practical optimum mold oscillation parameters (1) 随着非正弦因子α增大,渣道内最大正压增大,其增加幅度随着α增大而增大;渣道最大负压随着α增大而减小,其减小的幅度随α增大而减小。α的选择应使渣道内正负压力波动控制在合适的范围内,同时延长正滑脱时间以增加渣流量,并缩短负滑脱时间以提高铸坯表面质量。α的最佳值约为 0.2,渣道正负压都在合理范围内,且最大正负压差最小。 (2) 随着振幅增加,最大正负压都增加,有利于铸坯的脱模、裂纹愈合和增加渣流量。但动态压力波动范围增大,弯月面波动加剧而降低铸坯质量,在保证脱模和润滑的前提下,应尽量采用小振幅振动。振幅对最大正压有更大影响,当振痕较深时,应适当降低振幅;当发生脱模困难时,增加振幅是一种有效措施。 (3) 振频增加使最大正压明显增加,最大负压增加很小,增加振频对强制脱模、愈合拉裂的坯壳有重要作用。高速连铸结晶器采用高频小振幅振动可以有效脱模、防止拉裂和漏钢事故,但振频过高会影响铸坯表面质量。 (4) 随着拉坯速度增加,最大负压增加,可以增加保护渣的流量,而最大正压减小,不利于铸坯脱模和拉裂坯壳的愈合;因此,拉速提高,应适当增加振幅和降低振频,以增加最大正压保证脱模和防止拉漏事故发生。 [1] ZANG Xin-yang, WANG Xu-dong, MA Yong, et al.Investigation of friction force between mould and strand shell under sinusoidal and non-sinusoidal oscillation in continuous slab casting[J]. Steel Research International, 2008, 79(7):564-568. [2] LI Xian-kui, ZHANG Li-ping, YANG La-dao, et al. Dynamics study on new non-sinusoidal oscillation system of mold[J].Journal of Iron and Steel Research International, 2008, 15(S1):517-522. [3] ZANG Xin-yang, WANG Xu-dong, MA Yong, et al. The shell surface force caused by mould friction during slab continuous casting[J]. ISIJ International, 2008, 48(2): 170-174. [4] Shin H J, Kim S H, Thomas B G, et al. Measurement and prediction of lubrication, powder consumption, and oscillation mark profiles in ultra-low carbon steel slabs[J]. ISIJ International,2006, 46(11): 1635-1644. [5] MENG Xiang-ning, ZHU Miao-yong. Optimization of non-sinusoidal oscillation parameters for continuous casting mold with high casting speed[J]. Journal of Iron and Steel Research International, 2008, 15(S1): 510-516. [6] Takeuchi E, Brimacombe K. The formation of oscillation marks in the continuous casting of steel slabs[J]. Metall Mater Trans B,1984, 15(5): 493-509. [7] Kajitani T, Okazawa K, Yamada W, et al. Cold model experiment on infiltration of mould flux in continuous casting of steel: Simple analysis neglecting mould oscillation[J]. ISIJ International, 2006, 46(2): 250-256. [8] Kajitani T, Okazawa K, Yamada W, et al. Cold model experiment on infiltration of mould flux in continuous casting of steel: Simulation of mould oscillation[J]. ISIJ International, 2006,46(10): 1432-1441. [9] LEI Zuo-sheng, REN Zhong-ming, DENG Kang, et al.Amplitude-modulated magnetic field coupled with mold oscillation in electromagnetic continuous casting[J]. ISIJ International, 2006, 46(5): 680-686. [10] 孟祥宁, 朱苗勇. 连铸结晶器非正弦振动波形构造及参数研究[J]. 中国机械工程, 2007, 18(15): 1779-1783.MENG Xiang-ning, ZHU Miao-yong. Non-sinusoidal oscillation waveform conformation and parametrical research for continuous casting mold[J]. Journal of Chinese Mechanical Engineering, 2007, 18(15): 1779-1783. [11] 王宏明, 王振东, 李桂荣, 等. 连铸保护渣道动态压力计算模型及影响因素分析[J]. 北京科技大学学报, 2009, 31(6):777-781.WANG Hong-ming, WANG Zhen-dong, LI Gui-rong, et al.Impact factors analysis and mathematical model on dynamic pressure in mould flux channel[J]. Journal of University Science and Technology Beijing, 2009, 31(6): 777-781. [12] 孟祥宁, 朱苗勇, 刘旭东, 等. 高拉速连铸结晶器非正弦振动因子研究[J]. 金属学报, 2007, 43(2): 205-210.MENG Xiang-ning, ZHU Miao-yong, LIU Xu-dong, et al. Study on non-sinusoidal oscillation factor for continuous casting mold with high casting speed[J]. Acta Metallurgica Sinica, 2007, 43(2):205-210. [13] Lee G G, Thomas B G, Kim S H. Microstructure near corners of continuous-cast steel slabs showing three-dimensional frozen meniscus and hooks[J]. Acta Materialia, 2007, 55(20):6705-6712. [14] Sengupta J, Thomas B G, Shin H J. A new mechanism of hook formation during continuous casting of ultra-low-carbon steel slabs[J]. Metallurgical and Materials Transactions A, 2006, 37(5):1597-1607 [15] 雷作胜, 任忠鸣, 闫勇刚, 等. 软接触结晶器电磁连铸保护渣道的动态压力[J]. 金属学报, 2004, 40(5): 546-550.LEI Zuo-sheng, REN Zhong-ming, YAN Yong-gang, et al.Amplitude-modulated magnetic field coupled with mold oscillation in electromagnetic continuous casting[J]. Acta Metallurgica Sinica, 2004, 40(5): 546-550.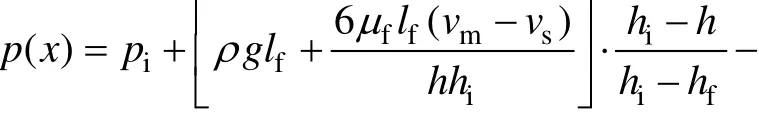
3 计算结果与分析
3.1 非正弦因子对振动速度及渣道压力的影响


3.2 振幅变化对渣道压力变化规律的影响
3.3 振频变化对渣道压力变化规律的影响
3.4 拉速变化对渣道压力变化规律的影响
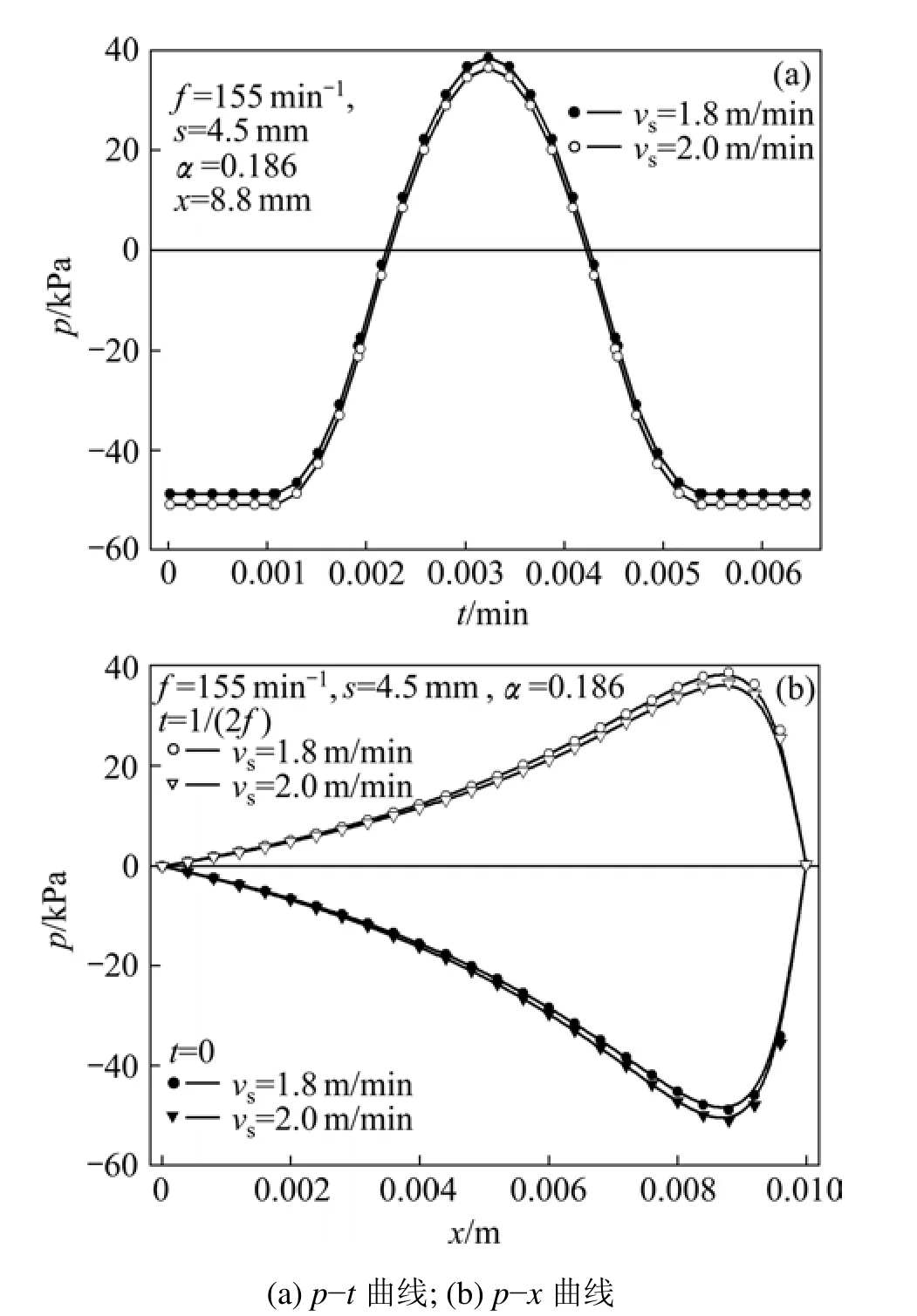
3.5 优化振动参数下保护渣道压力规律
4 结论

