关于Diophantine方程x2+4n=y3

王 振，张 慧

(安徽大学 数学科学学院，合肥 230039)

关于不定方程x2+4n=y3，n∈N已经有了不少研究工作［1-3］，其中n=0，1 时，潘承洞、潘承彪【1】在“代数数论”一书中关于方程x2+1=y3，x2+4=y3的整数解问题做了详细的证明，整数解分别是(x，y)=(0，1)，(x，y)=(±2，2)，(±11，5).n=2 时，2006 年廖江东［2］证明了x2+16=y3无整数解.黄勇庆［1］证明了不定方程x2+4n=y3(n∈N，x≡ 1( m od2 )，x，y∈Z)整数解仅有 (x，y，n) = ( ±11，5，1).此处在前几人证明的基础上证明了n≥3时，不定方程x2+4n=y3(n∈N，x≡ 0( m od2 )，x，y∈Z)的整数解为:(x，y，n) = ( 0 ，4k，3k)，(±2 ×8k，2 ×4k，3k+1 )，( ±11 ×8k，5 ×4k，3k+1)，k∈N*.至此此不定方程的全部整数解完全解决.

引理 1【1】x2+1=y3，x，y∈Z整数解仅有 (x，y) = ( 0 ，1).

引理 2【1】x2+4=y3，x，y∈Z整数解仅有 (x，y) = ( ±2，2 )，( ±11，5).

引理 3【2】x2+16=y3无整数解.

引理 4【3】x2+4n=y3(n∈N，x≡ 1( m od2 )，x，y∈Z)整数解仅有 (x，y，n) = ( ± 11，5，1).

定理1 不定方程:

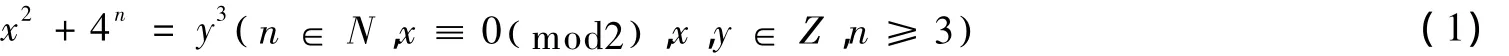
整数解仅有 (x，y，n) = ( 0 ，4k，3k)，( ±2 ×8k，2 ×4k，3k+1 )，( ±11 ×8k，5 ×4k，3k+1 )，k∈N*.

证明 当n=3k时，不定方程(1)即:

此不定方程整数解仅有 (x，y) = ( 0 ，4k).

当k=1时，式(2)即:

由式(3)易知x，y都是偶数，令x=2x1，y=2y1，x1，y1∈Z代入式(3)可得:

易知x1必为偶数，从而y1也必是偶数.令x1=2x2，y1=2y2，x2，y2∈Z代入式(4)可得:

易知x2为偶数，令x2=2x3，代入式(5)可得+1=(x3，y2∈Z).从而由引理1知上式整数解仅有(x3，y2)= ( 0 ，1 )，由x=8x3，y=4y2，可得式(3)整数解仅有 (x，y) = ( 0 ，4).

假设当k=i时，式(2)结论成立，即x2+43i=y3(x≡ 0( m od2 )，x，y∈Z，i∈N*).方程整数解仅有(x，y) = ( 0 ，4i).

当k=i+1时，式(2)即:

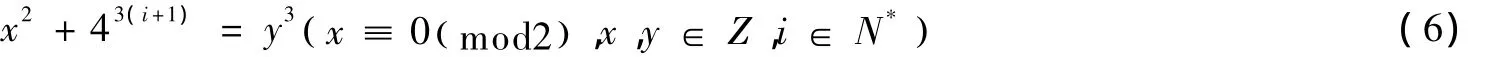
同式(3)证明过程易知:

其中，x=8x3，y=4y2，x3，y2∈Z.

若x3≡ 1 ( m od2)时，因为3i≥3，由引理4知式(7)无整数解.若x3≡ 0( m od2)时，由假设可知式(7)整数解仅有 (x3，y2)= ( 0 ，4i)，由x=8x3，y=4y2可得，式(6)整数解仅有 (x，y) = ( 0 ，4i+1).

当n=3k+1时，不定方程(1)即:

此不定方程整数解仅有 (x，y) = (±2×8k，2×4k)，( ±11×8k，5×4k).

当k=1时，式(8)即:

证明同式(3)，易知:

其中x=8x3，y=4y2，x3，y2∈Z.由引理 2 知，等式(10)整数解仅有 (x3，y2)= ( ±2，2 )，( ±11，5).由x=8x3，y=4y2可得式(9)整数解仅有 (x，y) = (±2×8，2×4 )，( ±11×8，5×4).

假设当k=i时，式(6)结论成立，即x2+43i+1=y3(x≡ 0( m od2 )，x，y∈Z，i∈N*)，方程整数解仅有(x，y) = (±2×8i，2×4i)，( ±11×8i，5×4i).

当k=i+1时，式(5)即:

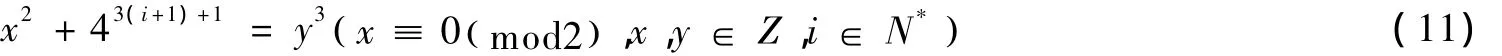
证明同(4)式，易知:

其中x=8x3，y=4y2，x3，y2∈Z.若x3≡ 1 ( m od2)时，因为3i+1≥4，由引理4知，式(12)无整数解.若x3≡0( m od2)时，由假设可知式(12)整数解仅有 (x3，y2)= (±2 ×8i，2 ×4i)，( ±11×8i，5×4i).由x=8x3，y=4y2可得，式(11)整数解仅有 (x，y) = (±2×8i+1，2×4i+1)，( ±11×8i+1，5×4i+1)，从而结论成立.

当n=3k+2时，不定方程(1)即:

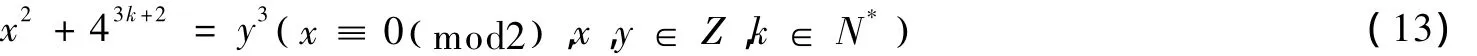
此方程无整数解.

当k=1时，式(13)即:

证明同式(3)，易知:

其中x=8x3，y=4y2，x3，y2∈Z.

由引理3可知，式(15)无整数解.由x=8x3，y=4y2，从而式(14)无整数解.

假设当k=i时，式(13)结论成立，即x2+43i+2=y3(x≡ 0( m od2 )，x，y∈Z，i∈N*)，方程无整数解.

当k=i+1时，式(13)即:

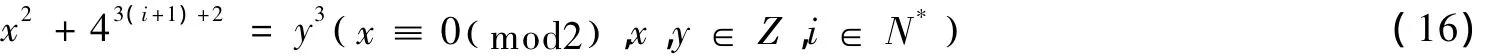
证明同式(4)，易知:

其中x=8x3，y=4y2，x3，y2∈Z.

若x3≡ 1 ( m od2 )时，因为3i+2≥5，由引理4知，式(17)无整数解.若x3≡ 0( m od2)由假设可知，式(17)无整数解，由x=8x3，y=4y2，从而式(16)无整数解，结论成立.

综合以上3种情况可知定理1成立.

［1］潘承洞，潘承彪.代数数论［M］.济南:山东大学出版社，2003

［2］廖江东，柳杨.关于不定方程x2+16=y3［J］.四川理工学院学报:自然科学版，2007，20(2):4-5

［3］黄勇庆.关于不定方程 x2+4n=y3［J］.四川理工学院学报:自然科学版，2007，20(1):26-27

［4］赵开明.关于不定方程 x2-53=4y5［J］.重庆工商大学学报:自然科学版，2008，25(4):345-346