一种随机选择的扰动随机化回答技术

洪志敏 ，闫在在 ，韩 英 ，魏利东

（1.内蒙古工业大学 理学院数学系，呼和浩特 010051；2.内蒙古呼和浩特统计局城乡社会经济抽样调查队，呼和浩特 010023）

0 引言

在当今的社会调查中，我们常常会遇到许多关于敏感性问题的调查，如未婚女子的堕胎次数、是否吸毒、家庭收入的多少等等。对于这些问题的调查，如果采用直接调查的方法，出于对自身隐私的保护，被调查者可能拒绝或作出不真实回答。为了使被调查者配合调查，Waner[1]1965年首先引入了敏感性问题的随机化调查方法，揭开了随机化调查的序幕。之后 Simmons[2](1967)、Mangat[3][4](1990,1994)、Kuk[5](1990)、Singh[6](2002)等一些学者进一步发展了随机化回答技术。这些学者提出的调查方法解决的是定性敏感性问题的调查，即估计总体中具有敏感特征个体所占的比例。对于定量敏感性问题的研 究 ，Greenberg[7][8](1969,1971)、Eichhorn 和 Hayre[9](1983)、Gupta[10](2002)、Bar_Lev[11](2004)等提出了一些可供选择的随机化调查方法。

设X表示对定量敏感问题的回答值，S表示一个与X相互独立的正的随机数，且S的均值与方差已知，分别记为θ，γ2。回答者所产生的回答是敏感变量X与随机数S的乘积。调查者最终收集到的是个体关于敏感指标的扰动回答。样本中的每一个个体使用某种随机化装置产生一个随机数S，调查者不知道被调查者产生的随机数S。这里随机数S被EH称为扰动随机变量。使用简单随机有放回抽样(SRSWR)方法从总量为N的总体中抽取容量为n的样本，则样本中的第i个个体报告的回答值为zi=xisi,样本均值为E-ichhorn和Hayre(1983)对总体的敏感指标X的均值给出一个如下的无偏估计量：

方差为：

2002年，Gupta等人在Eichhorn和Hayre(1983)扰动回答模型的基础上给出一种可选择的随机化调查技术，在此模型下，每个个体选择如下两类问题中的一类：

(1)回答者报告敏感指标真值：

(2)回答者报告扰动回答XS,其中S为事先产生的与X相互独立的扰动随机数。且满足E(S)=θ=1。调查者收集到的关于敏感指标X的扰动回答是Z=XSW,其中W为示性随机变量，即令P0为个体报告扰动回答的概率，则E(W)=P0。调查者根据所调查问题的敏感程度来选择设计参数的P0值。如果所调查的问题较为敏感，此时人们倾向于使用扰动回答，则调查者会选择一个较大的值。如果问题是非常不敏感的，此时人们倾向于作直接回答，则调查者会选择一个很小的设计参数。容量为n的简单随机有放回样本(SRSWR)中的第i个个体报告的回答值为

方差为：

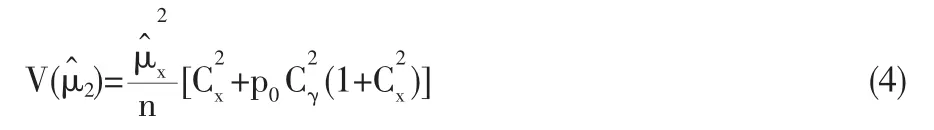
Bar-Lev,Bobovitch和Boukai2004年给出一种改进的扰动回答模型，设X是所要调查的定量敏感指标，Y是一个分布已知的扰动随机变量，X与Y相互独立，P0是调查装置设计参数。

被调查者遵循如下的随机化回答原则：Z=XSW其中W为示性随机变量，即令P0为个体报告扰动回答的概率，则 E（W）=P0。其中 E(S)=θ,V(S)=γ2为已知。使用简单随机有放回抽样(SRSWR)的方法从容量为N的总体中抽取容量为n的简单随机样本，样本中n个个体给出的随机化回答值为Bar-Lev 等给出的敏感指标均值的无偏估计量为：

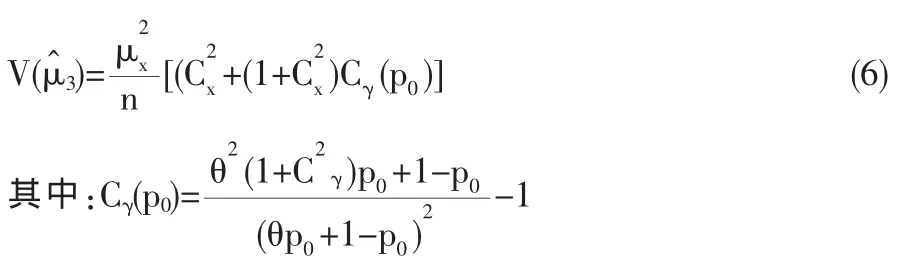
在所有的随机化回答技术中，个体参与调查的合作程度均依赖于调查装置对个体作出回答的保密程度，装置对个体隐私的保密性越好，个体越容易配合调查。另一方面，如果装置对个体的保护程度提高了，那么装置的调查效率就会降低。因此装置对个体的保护度与装置的调查效率之间存在着不可调和的矛盾。为了在保护度与效率之间建立一种合理的平衡，已有很多学者[12～14]在这方面作出了研究。

1 模型构造

在使用已有模型进行随机化调查时，装置的设计参数p0是调查者根据所调查问题的敏感程度事先确定的。因此个体仍然担心自身的隐私会被暴露，在作出回答时心存疑虑。本文在已有随机化模型的基础上给出一种随机选择的扰动回答模型，给出的模型不仅可以提高个体参与敏感问题调查的积极性，且在调查效率上也有所得益。

在本文提出的调查装置中，装置设计参数p不是事先确定的，而是由被调查者随机产生且不为调查者所知的，仅p的分布是已知的。在调查之前由第一位被调查者根据p的分布随机产生一个设计参数p*，剩余的被调查者均使用这个随机设计参数p*，下面我们给出具体的随机回答模型。

使用简单随机有放回抽样(SRSWR)方法从总量为N的总体中抽取容量为n的样本个体，第一个样本个体使用某种随机化装置(计算机，带有时针的圆盘等)产生一个分布已知的随机设计参数p*,概率分布为f(p)。剩下的n-1个个体均使用第一个个体产生的随机设计参数p*。样本个体报告的回答值为

令E1，V1表示对p*的随机性求期望和方差；E2,V2表示固定p*值对抽样的随机性求期望和方差；E3,V3表示固定P*值对回答的随机性求期望和方差。样本个体报告的回答值zi的期望为 E(zi)=E1E2E3(zi)=E1E2(p*xi+(1-p*)xi)=E1E2(xi)=μx，则本文模型提出的对μx的一个无偏估计量为：

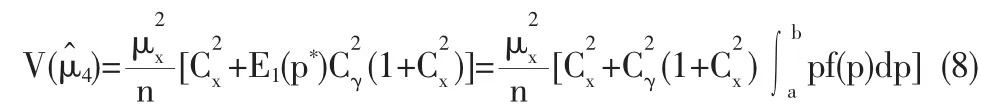
其中f(p)(a＜p＜b)为设计参数p*的概率密度函数。

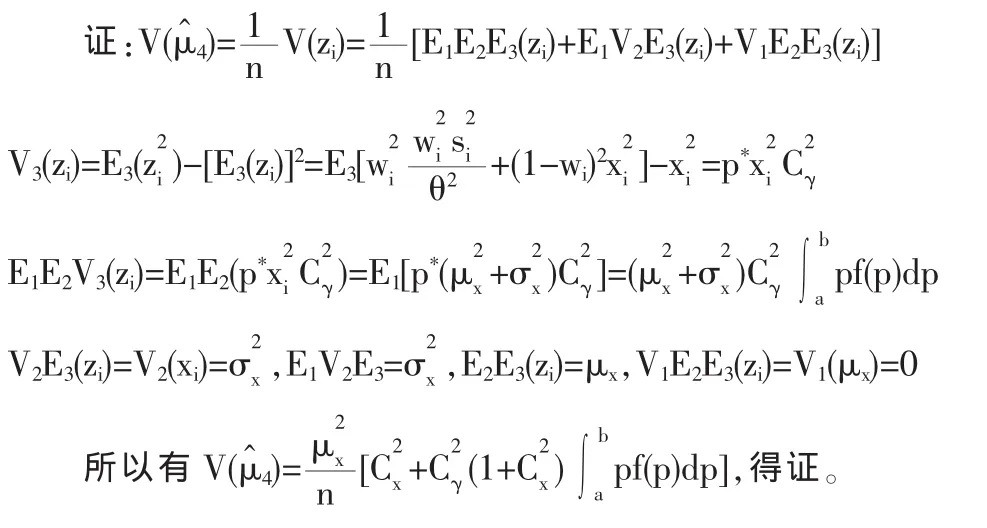
2 估计量的效率

选择p*的不同概率密度函数f(p)，对应着估计量μ^4的不同效率。这里我们选择f(p)为如下两种形式对估计量μ^4的效率进行讨论，对于f(p)的其他选择会有类似的讨论。

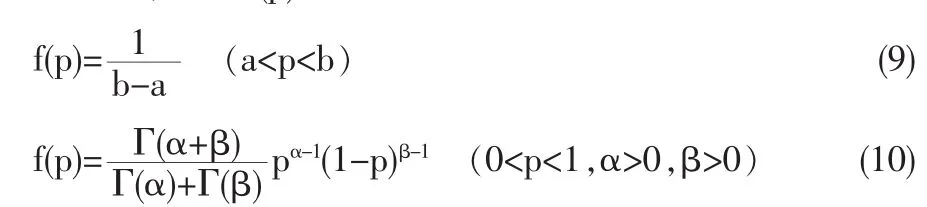
根据定义(7)式有如下结论：

定理3 根据(9)式来定义p*的概率密度函数f(p)，估计量的方差为：

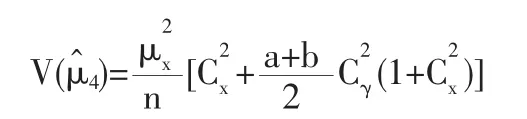
在Gupta(2002)模型中，对于任意的调查设计参数0＜p0＜1有如下结论成立：

推论 1 取 a=p0(1-g)，b=p0，0＜g＜1，0＜p0＜1，则本文所提出的调查模型在效率上优于Gupta(2002)模型。这里也可以选择其他合理的a和b的值使得本文提出模型优于Gupta(2002)模型。

根据定义(8)式有如下结论：

定理4 根据(10)式来定义p*的概率密度函数f(p)，估计量的方差为：

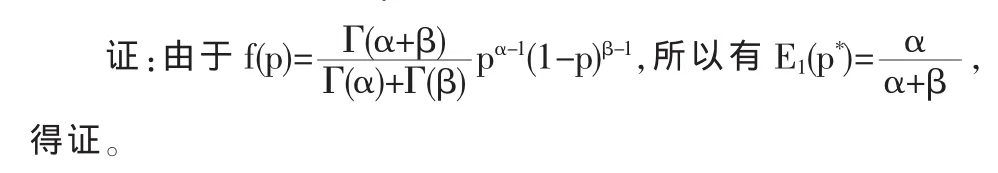
推论 2 取 α=gp0，β=1-α，0＜g＜1，0＜p0＜1，则本文所提出的调查模型在效率上优于Gupta(2002)模型。在这种情形下，我们也可以选择其他恰当的α和β值来获得更高的调查精度。

由以上的结论可以得出，本文给出的估计量μ^4在精度上要优于Gupta(2002)模型中给出估计量的精度。另一方面，由于本文给出调查模型的设计参数是随机产生的，调查者并不知道被调查者使用的是哪一个设计参数的回答模型，即调查者不知道被调查个体是以多大的概率给出扰动回答，因此，模型在很大程度上保护了个体的隐私，从而提升了个体参与调查的积极性。

3 结论

在Gupta(2002)模型中，假定扰动变量的总体均值为1，即E(S)=1，这简化了估计量及其性质的理论推导，但对估计量的精度也产生了影响。本文给出的随机化模型扰动变量的总体均值可以不为1，这并没有使估计量及其性质的理论推导复杂化。本文提出的随机选择的扰动回答模型无论是在调查精度上还是在对个体隐私的保护上都是一种可供选择的调查模型。

[1]Warner S L.Randomized Response:A Survey Technique for E-liminating Evasive Answer Bias[J].J.Amer.Statist.Assoc.,1965,(60).

[2]Horvitz D G,Shah B V,Simmons W R.The Unrelated Question Randomized Response Model[C].Proceeding of the Social Stat.Sec.Amer.Stat.1967.

[3]Mangat N S,Ravindra Singh.An Alternative Randomized Re-Sponse Procedure[J].Biometrika,1990,(77).

[4]Mangat N S.An Improved Randomized Response Strategy[J].R Statist Soc.1994,(56).

[5]Anthony KUK YC.Asking Sensitive QuestionsIndirectly[J].Biometrika,1990,(77).

[6]Sarjinder Singh.A New Stochastic Randomized Response Modle[J].Metrika,2002,(56).

[7]Greenberg B G,Abul-Ela E L A.The Unrelated Question Randomized Response Model:Theoretical Framework[J].Amer.Stat.Assoc,1969,(64).

[8]Greenberg B G,Kuebler R R,Abernathy J R,Horvitz D G.Application of the Randomized Response Technique in Obtaining Quantitative Data[J].Amer.Statist.Assoc,1971,(66).

[9]Eichhorn B H,Hayre L S.Scrambled Randomized Response Methods for Obtaining Sensitive Quantitative Data[J].J.of Statistical Planning and Inference,1983,(7).

[10]Gupta S,Gupta B,Singh S.Estimation of Sensitivity Level of Personal Interview Survey Questions[J].Statist.Plann.Infer.,2002,(100).

[11]Bar-Lev S K,Bobovitch E,Boukai B.A Note on Randomized Response Models for Quan-titative Data[J].Metrika,2004,(60).

[12]Hong Zhimin.Estimation of Mean in Randomized Response Surveys when Answers are Incompletely Truthful[J].Model Assisted Statistics and Applications,2006,(1).

[13]闫在在，聂赞坎.随机化策略的公平比较[J].数学物理学报，2004,(24).

[14]洪志敏，闫在在.基于相同保护度的随机化装置效率比较[J].工程数学学报,2008,(25).