两分类不平衡数据的Boosting算法

宋 捷 ，吕晓玲 ，吴喜之 ,b

(中国人民大学a.统计学院；b.应用统计研究中心，北京 100872)

0 引言

分类是统计应用中的一个重要领域。它通常是通过训练数据学习得到一个分类器，然后再用这个分类器对需要预测的数据进行预测。目的是得到较好的预测，也就是得到更小的预测误差。以两分类为例，预测误差是这样两部分之和，一部份是把1类分为2类发生的错误，另一部分是把2类分为1类发生的错误。但是有时这个预测误差越小却不能说明这个分类就好。比如：有一个两分类的总体，两个类在总体中的比例为（0.10，0.90），有一个分类器的预测误差为0.19，两个类各自的类内预测误差为（0.9,0.1）；另一个分类器的预测误差为0.22，两个类各自的类内预测误差为（0.4,0.2）。第一个分类器的预测误差更小，但是它把第一个类中的样品几乎都分错了。第二个分类器虽然预测误差稍大，但是在两个类中的预测误差都比较小。由此可见，用总体的预测误差来评价分类器的好坏此时已经不妥。像这种各个类在总体中的比例相差很大的数据我们称为不平衡数据。实际中我们也会遇到很多这样的数据。比如在诊断病人时，我们有的只是很少的病例，而绝大多数人都是健康人。这时病人和健康人就是比例相差很大的两个类。诊断病人时我们希望最好把病人都诊断为病人，健康人都诊断为健康人。但是不管怎样都会有错分发生，而且把病人诊断为健康人的风险总是远远高于把健康人诊断为病人。也就是说我们希望的是两个人群中各自的错分都要比较小。我们就想到为什么不同时减小每个类内部的预测误差，而不仅仅是减小所有类的预测误差。也就是说我们需要消除两个类之间的不平等性。

在此之前，有很多人通过调整各个类在总体中的比例来处理不平衡数据。Xingye Qiao和Yufeng Liu[5]提出一种对每个类的样品错分率迭代加权的方法。本文也将通过减小各个类内部的预测误差的想法出发提出一种自适应的处理不平衡数据的Boosting算法Baboost。

1 Adaboost算法

Adaboost算法是一种集成的分类算法。因为其良好的分类能力与抵抗过拟和的能力而受到大家的广泛应用。Breiman[1]用Boosting技术来提高一次分类的能力，通过集成的方法有效地减小偏差，从而提高单个不稳定分类的预测误差。Adaboost算法的运行机制也一直是大家研究的热点。目前流行的观点是由Friedman等人[2]提出的，认为Boosting是一种可加模型。基于不同的损失与不同的组合方式，研究者们提出了很多不同的Boosting算法。

Adaboost算法通过不断迭代优化的方法来进行分类。考虑到解释变量与被解释变量的全概率，不管类与类之间数据多少的比例，通过减小总的分类误差来进行分类。但是当类与类之间数据严重不平衡时，Adaboost算法的误差会只由数据少的那类带来，可能那一类的数据完全被错分。之所以出现这个问题的原因是Adaboost算法是基于类之间地位平等的时候的一种分类算法。以两分类为例，当以损失采用指数损失时，最优解是我们可以看到，这个最优解等价于也就是x与y的全概率之比。但是当遇到两个类的数据比例相差很大时，这个解就会受到很大影响。因为当很小或者很大时，最优解就会受到很大影响，而的作用不容易显露。

W.Fan 等人(1999)[4]，Nitesh V.Chawla 等人(2002)[3]等人都提出一些通过调整不同类的权重的方法来改进Adaboost，得到比Adaboost小的预测误差。但是他们的方法都不是直接从各个类内部的错误率出发来更新权重，而且其中的参数也比较难于的确定。

2 Balanced Adaboost算法

Adaboost的目标是减小错分误差。错分误差包括两部分：一部分是把属于1类的样品分为0类，一部分是把属于0类的样品分为1类。Adaboost将这两种误差看作是同等地位的误差。从而目标就是减小这两种误差之和。但是在很多实际问题中两种错误的地位是不同的。比如在医学中，将一个没有病的人诊断为病人带来的风险就远远小于将有病的人诊断为没有病。此时两个类之间不平等正是由数据量的差别所带来的，需要调整两个类的权重。这里我们通过各个类内部的预测误差来自适应地调整权重，提出一种新的自适应的处理不平衡数据的Balanced Adaboost算法，简称：Baboost。对于两分类而言，算法如下。

算法1：

输入: 训练集(X1,Y1),(X2,Y2),…(Xn,Yn)，Yi∈{-1,+1}

(1)给出初始化权重ω0=1/n，H初值为0；

(2)放回地以概率分布为ωi对所有样品进行抽样(i=0,1,2,…，n)，用抽出的样品得到一个弱分类器ht:Xn→{-1,+1},这里假设1类是多数类,-1类是少数类；

(3)计算两种错分率

当ht(Xi)=1时

et1=∑Dt(i)*I(ht(Xn)≠Yi∩ht(Xi)=1/∑Dt(i)*I(ht(Xn)=1)

计算ct1=ln(1-et1)/et1)

当ht(Xi)=-1时

ett-1=∑Dt(i)*I(ht(Xi)≠Yi∩ht(Xi)=-1)/∑Dt(i)*I(ht(Xn)=-1)

计算ct1=ln(1-et1)/et1)

更新H=H+ctht

更新权值:如果 ht(Xi)≠Yi，且 ht(Xi)=1，Dt+1(i)Dt(i)exp(ct1)

如果 ht(Xi)≠Yi，且 ht(Xi)=-1，Dt+1(i)Dt(i)exp(ct1)

如果ht(Xi)=Yi,Dt+1(i)=Dt(i)，将两类权重分别归一化后再归一化；

(4)重复B,C步次；

(5)输出 sign(H(x))。

从上面的算法程序中我们可以直观地看到，对于两类样品分别计算了类内的错分误差，数据多的那类错分率相对于数据少的那类的错分率要低。这样在下一步更新权重时，对于分错的样品就不再是同样的更新方式了。分错的样品的权重都将给以更高的权重，权重都要增加。但是他们不再增加相同的量。数据多的那类被错分的样品的权重增加量比数据少的那类被错分的样品的权重增加量要小。同时，每个分类器在划分1类与-1类的准确性上也做了区分，不再是同样的划分能力。如果该分类器把原本是1类的样品划分为-1类的概率很高，即偏大，那么该分类器将样品划分为-1类的准确性低，此时相应地就偏小。如果该分类器把原本是-1类的样品划分为1类的概率很高，即偏大，那么该分类器把样品划分为1类的准确性低，此时相应地就偏小。

3 实验结果

3.1 数值试验

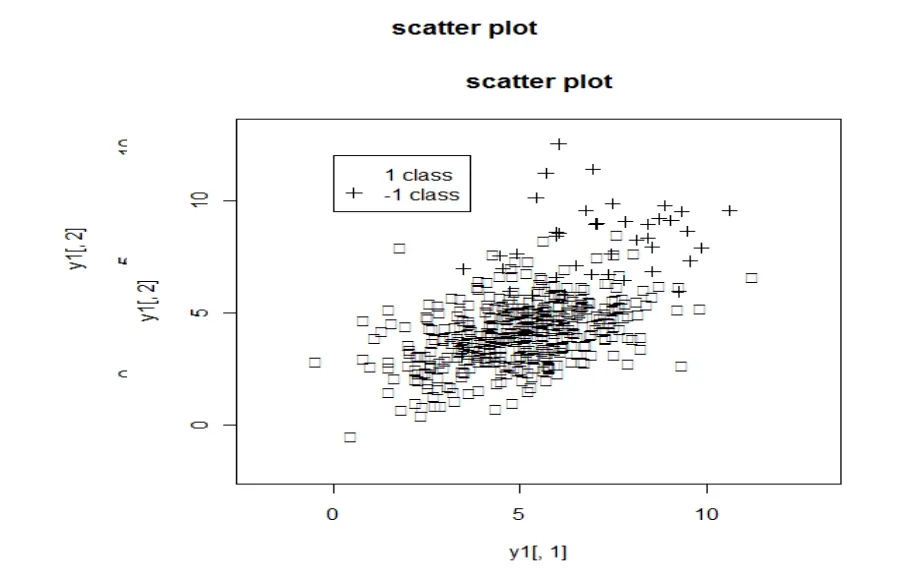
图1 数据散点图

我们随机选取其中的一半数据作为训练集，剩下的作为测试集。下面的结构都是计算了100次的平均结果。运算中，还可以依据实际情况自己调整的取值为上面算法描述中的1/100，1/200等。ct1越小，-1类的错分率越低。下面的结果是取ct1/500的结果。Adaboost算法与Baboost算法结果如表1。

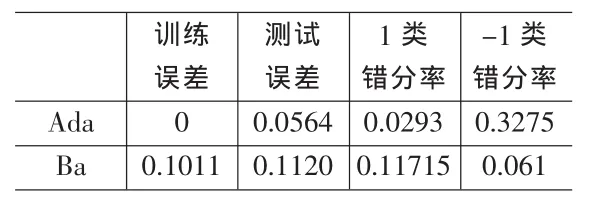
表1 模拟数据试验结果

从上面的结果中我们可以看到，只从测试误差上来看，Adaboost的测试误差比Baboost小了49.7%。但是我们把测试误差分开来看，可以看到，测试误差中的90%都是由-1类的错分所带来的。也就是说此时Adaboost在划分-1类的样品时所发生的错误相当大，几乎是划分1类样品发生错误的15倍。而Baboost在-1类上的错分率比Adaboost在-1类上的错分率小了81.4%，并且Baboost在划分-1类样品时所发生的错误比划分1类样品发生错误还小。图2是两种算法分别计算100次在两个类中的错分率。

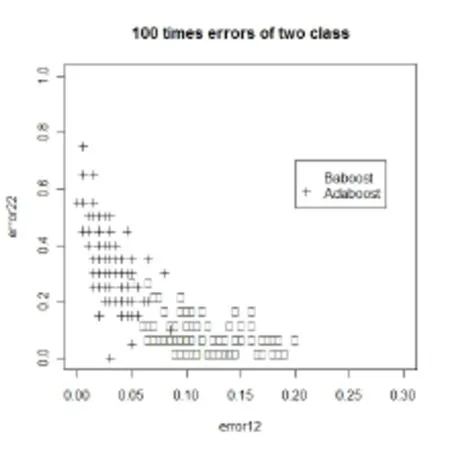
图2 100次类内误差

横轴是在1类中的错分率，纵轴是在-1类中的错分率。从图2可以看到，Baboost的错分率点几乎 100%都在点(0.2,0.2)的右下方，而Adaboost的错分率点只有20%左右在点(0.2,0.2)的右下方。我们当然希望一个算法能使得两个类的错分类率都比较低，而不是只是某一类的错分率较低。

3.2 实际应用

这里我们将上述算法应用到Satimage数据集。该数据集来源于UCI机器学习网站http://www.ics.uci.edu/～mlearn/。该数据的分类目标是决定是否一个病人有甲状腺功能减退的症状。该数据集包括7200个样品，21个自变量，因变量为3分类的变量。自变量中有15个属性变量，6个连续变量。其中三个类的样品个数分别为：166，368，6666。我们选择其中200个样品做为训练集，200个样品做为测试集。训练集和测试集中三个类的样品个数分别为：5，10，185，保持了原来数据各个类之间的比例。

试验中，我们选取Ct3/200，重复试验了100次，每次的训练集与测试集都是随机选取。表2结果是100次的平均结果。

表2 hyroid数据试验结果

从表2可以看到，如果用Adaboost算法处理这个数据时数据少的类的错分率比数据多的类的错分率高很多。而用Baboost对数据进行处理将会大大改善结果，尤其是在一类和二类数据的划分上。而且我们这个算法比Xingye Qiao和Yufeng Liu[3]提出的方法的每个类的错分率都要低。他们的方法在三个类上的错分率分别为：0.153，0.187，0.201。原因是我们对每个的基分类器都要加权，考虑每个基分类器的分类能力。而他们的方法不考虑每个基分类器的分类能力。

4 结论

从上面的试验中我们可以看到，当数据不平衡时，Baboost在总的预测误差上会比Adaboost要高一点。但是总的预测误差此时用来评价模型的好坏已经不完善了。当我们分别用类内的预测误差来评价时，发现此时Baboost比Adaboost的预测性能更好。尤其是在数据偏少的那些类。而在实际问题中，我们经常关心的很可能正好是数据少的那些类，所以减少少量数据那类的类内误差更实际有效。

算法的不足是没有对的取值进行优化，只是简单的选择1/500或者1/200。这可以在以后的工作中加以进一步讨论。

[1]Breiman L.Bias,Variance,Arcing Classifiers,Tech.Rep.460[M].California：University of California，1996.

[2]Friedman,J.H.,Hastie,T.,Tibshirani,R.Additive Logistic Regression:A Statistical View of Boosting[J].Annals of Statistics,2000,28.

[3]N.V.Chawla,K.W.Bowyer,L.O.Hall,W.P.Kegelmeyer.SMOTE:Synthetic Minority Over-Sampling Technique[J].Journal of Artificial Intelligence Research,2002,16.

[4]W.Fan,S.Stolfo,J.Zhang,P.Chan.Ada Cost:Misclassification Cost-Sensitive Boosting[C].Proceedings of 16th International Conference on Machine Learning,Slovenia,1999.

[5]Xingye Qiao,Yufeng Liu.Adaptive Weighted Learning for Unbalanced Multicategory Classification[M].USA：University of North Carolina,2008.