基于GARCH模型的CVaR信贷风险度量方法研究
刘琦铀,张能福,刘铁生
(1.五邑大学 管理学院,广东 江门 529020;2.江西现代职业技术学院,南昌 330095)
0 引言
尽管VaR方法自其推出以来一直受到金融资产管理者的青睐,但随着国内外学者的不断探索和实际运用部门的实践证明,VaR方法仍存在其自身的局限性。由于该模型不是一致性风险度量,没有考虑当VaR值超过时损失究竟是多少的问题。因此,当真实损失超过了VaR的度量时,无法进一步识别风险是可以忍受的还是灾难性的。本文拟针对VaR的弱点,对Rockafeller和Uryasev于1999年对VaR模型加以修改,提出条件风险价值CVaR(Conditional Value-at-Risk)的概念。
1 相关模型基本原理方法及其特点
1.1 VaR的风险控制原理方法及其特点
1.1.1 VaR的风险控制原理
VaR是指在某一特定的持有期内,在给定的置信水平下,给定的资产或资产组合可能遭受的最大损失值。其数学定义式为:

其中,ΔP为金融资产在持有期Δt内的价值损失;VaR为置信水平c下的风险价值;c为置信度或置信水平(一般取95%或99%)。在给定的持有期和给定的置信水平下,VaR给出了其最大可能的预期损失。也就是说,可以用c的概率保证,其资产或资产组合的损失不会超过VaR值。现以某证劵公司为例对VaR值的含义加以说明。假设该公司1994年每日的VaR值,在99%的置信区间内平均为370万美元。这意味着,每天因市场风险而导致损失超过370万元的概率只有1%,即平均100个交易日才可能出现一次这样的情况。换句话说,我们可以可以用99%的概率保证,该银行下一个交易日内的损失不会超过370万元。
1.1.2 VaR的计算方法
假设投资组合的期初价值为p0,Δt为该投资组合的持有期,R为该投资组合持有期内的收益率,假设收益率R的期望值、标准差和收益率最小值分别为μ、σ和R*,则根据VaR的定义:在一定置信水平下,该投资组合在未来一段时间的持有期内的最大可能损失为:
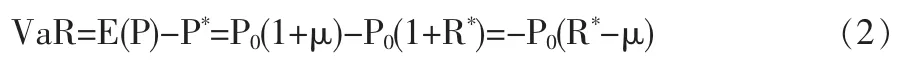
由以上定义可知,计算VaR即相当于计算组合最小价值P*或最低收益率R*。考虑投资组合持有期内收益率所服从的随机过程,假定其未来收益率的概率密度函数为f(P),则对于某一置信水平c下投资组合的最低值P*,有:

无论分布是离散的还是连续的,厚尾还是瘦尾,该表达方式都是有效的。
1.1.3 VaR模型的优缺点及CVaR的产生
VaR自上世纪90年代初期问世以来,曾以其独有的特点颇受金融资产管理者的青睐。但随着随着时代的发展和国内外学者的不断探索、运用,其不足之处也逐渐显现。具体来讲,其优缺点主要表现如下:
(1)VaR的优点
①VaR把对未来损失的大小和该损失发生的可能性结合起来,不仅让投资者知道该损失发生的可能性,而且能度量损失可能造成的最大的规模。同时,通过调节不同的置信水平,可以得到相应的VaR值大小,这样大大的方便了不同管理需要。
②与以往风险管理方法对比,该模型的显著特点主要表现在它是事前计算风险,而非事后衡量风险的大小;不仅能计算单个金融工具的风险,还能计算由多个金融工具组成的投资组合的风险。这一特点是传统金融风险管理所不及的。
③VaR不仅应用面相当广泛,而且可以把不同类型的风险大小以统一的标准尺度来衡量。它适用于综合衡量包括利率风险、汇率风险、股票风险以及商品价格风险和金融衍生工具在内的各种市场风险。这使得金融机构可以用一个具体的指标数值(VaR)来综合反映整个金融机构或投资组合的风险状况,这不仅大大方便了各金融机构最高管理层对机构内部风险的控制与管理,而且,监管部门也得以对金融机构的市场风险资本准备金提出相应统一的要求。
(2)VaR的局限性
VaR不是一致性风险度量,不满足次可加性。因此用VaR来度量风险时,证劵组合的风险大小不一定小于各证劵风险之和,这与投资组合具有分散风险的特点相违背,不符合基本的经济学原理。
VaR不满足凸性,从数学意义上讲,不满足凸性的函数可能存在多个极值,即局部最优非整体最优,故基于VaR对证劵组合进行整体上优化时,存在一定的障碍。
VaR仅给出了一个阈值,虽能以较大概率保证损失不超出分位数,但对极端事件的发生却缺乏预料与控制,既不能对尾部风险进行控制。VaR只被设计用于度量非正常但属一般性的市场波动所带来的风险,而对于市场因素异常罕见的极端波动所导致的损失VaR无法预知。例如,两种资产的VaR值相同,而超过VaR值的损失却不相同,此时VaR就无法来度量这两种资产的风险。
为了克服VaR的不足,Rockafeller和Uryasev于1999年对VaR模型加以修改,提出了条件风险价值CVaR(Conditional Value-at-Risk)模型,该模型传承了VaR模型的优点的同时又克服了其缺点。
1.2 CVaR的风险控制原理
条件风险价值 CVaR(Conditional Value-at-Risk),也称条件在线价值或者平均超值损失,是指超过VaR的损失的期望值,即在一定时间t内,在一定的置信水平c下,投资者对收益分布尾部1-c部分的期望值。其数学表达式为:
CVaR=E(L|L≥VaR) (4)
CVaR是指损失超过VaR的条件均值,它代表了超额损失的平均水平,反映了损失超过VaR时可能遭受的平均潜在损失的大小。
1.3 CVaR的计算方法
假设x是决策向量,x∈X;y是代表不确定因素的随机向量,y∈Y;对每一个x,相应的y的损失函数是f(x,y),那么f(x,y)不超过阈值(临界值)ξ的概率为:

若置信水平为c,c∈(0,1),VaRc可表示为:

VaR表示的是最大损失超过或等于的数值的概率为(1-c)的最小损失值,而CVaR定义的是最大损失值超过或等于的数值的概率为(1-c)的平均损失值,可表示为:

由以上公式可以得到:由于 Φc(x)≥ξc(x),可见,CVaR>VaR,VaR仅给出了一个阈值,虽然它能以较大概率保证损失不超出的分位数,但对极端事件的发生即尾部风险却缺乏预料和控制,而CVaR则能够对尾部风险进行良好的控制。CVaR与VaR相比考虑了损失尾部的分布,是一个更保守、更谨慎的风险度量方法。
2 基于GARCH模型的CVaR信贷风险实证分析
从以上有关VaR和CVaR的定义和计算方法中我们得知,VaR和CVaR方法的本质是对证券组合价值波动率的统计测量,其核心在于构造证券组合价值变化的概率分布,基本思想是利用资产组合价值的历史波动信息来推断未来情形,只不过对未来价值波动的推断给出的不是一个确定值,而是一个概率分布。因此计算他们的关键在于对金融资产收益率序列拟合一个合适的分布。传统方法对于此问题的研究大多简单地假设收益波动服从正态分布,而目前许多研究发现金融资产收益率时间序列不完全服从以上分布的假设,而是具有尖峰厚尾的特性,其波动具有聚集性和时变性,并且具有杠杆效应。为了刻画尖峰厚尾等金融时间序列所常有的性质,本文提出用GARCH模型来捕获金融资产时间序列这一特性。
2.1 GARCH模型的基本思想原理
为了充分地描述金融资产收益率的波动特性,在原有的ARCH模型基础上,Tim Bollerslev在1986年该模型中增加了q个自回归项,称为推广的ARCH(GARCH)模型。该推广的模型解决了原有模型固有的缺点,使待估参数大为减少,并且提高了计算的准确性。GARCH模型的一般表达式为:

第一个方程是建立在ARMA模型基础上的均值方程,rt为收益率序列,μt为收益的无条件期望值,目的是过滤掉时间序列的线性相关。第二个方程为条件方差方程,ai为滞后期参数,βj为方差参数,其中=Var(εt|φt-1),φt-1是 t-1 及 t-1时刻之前的全部信息,这里可以理解为过去所有残差的正加权平均,这与波动率的聚集效应相符合,即波动较大的地方往往也跟随着较大的波动,波动较小的地方往往也跟随较小的波动。
在GARCH模型中残差分布通常有三种:正态分布、学生t分布和广义误差分布(Generalized Error Distribution,GED)。以往的分析过程中,我们通常假设收益率残差分布服从正态分布,但正态性不足以反映收益率的尖峰厚尾性,因此Nelson和Hamilton等提出学生t分布和广义误差分布来反映金融时间序列这一特有的性质。正态分布、学生t分布和广义误差分布其密度函数分别为:

其中 Γ(·)为伽马函数,v为自由度,在 t分布中,当 v趋近与时,t分布收敛于正态分布;而在GED分布中,当v<2时,GED表现为厚尾,当v=2时,GED为正态分布,当v>2时则表现为瘦尾。
2.2 基于GARCH模型的CVaR计算过程
利用GARCH模型计算出标准差σt,我们可以得到相应的t时刻VaR的计算公式:

其中,pt-1是第t-1日的结算价格,σt为时变方差,f(q)为某一置信水平c下的分位数,由定义可知,CVaR为损失大于某个给定的VaR值条件下的期望损失,因此,若用a表示对应于某一置信水平c的分位数,用q表示大于a的分位数,则CVaR可通过下式求出:

其中,pt-1是第t-1日的结算价格,σt为时变方差,f(q)为收益率序列服从分布的密度函数,a为某一置信水平c下的分位数。由于正态分布、广义误差分布、学生t分布和其密度函数上面已给出,因此,三种不同分布下CVaR值分别为:

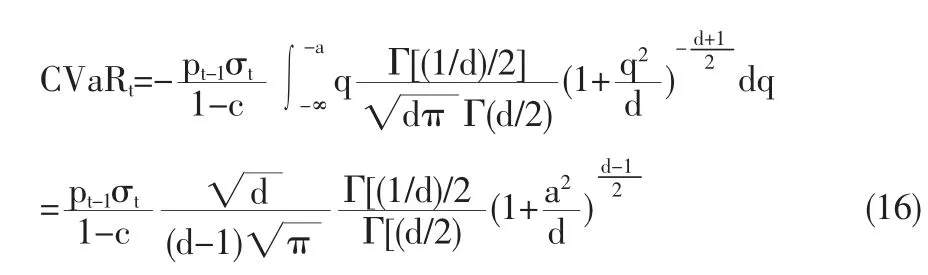
2.3 CVaR模型的准确性检验及结果分析
CVaR模型的准确性检验是指CVaR模型的测量结果对实际损失的覆盖程度。例如,假定给出了95%置信度下的CVaR,则CVaR模型的准确性是指实际损益结果超过CVaR的概率是否小于5%。通行的方法是Kupiec(1995)提出的失败频率检验法。假设样本总数为N,实际损失超出CVaR的估计的天数为P记为失败,失败的期望概率为1-c,若溢出率即失败率说明模型低估了风险;若固然表明模型的预测结果覆盖了实际的损失,但是太小的η却说明模型的估计过于保守。
3.4 基于GARCH模型的CVaR方法实证分析
为了突出样本数据的选取具有代表性,使实证研究更具说服力。本文以上证180数据为研究对象,对我国股票市场风险进行实证分析。选取样本范围为2003年1月到2004年5月,共334个交易日数据。分析与计算借助Matlab6.5软件完成。收益率采取连续复合收益(对数收益):

其中pt和pt-1分别为上证第t和t-1个交易日收盘价。首先根据原始数据由MATALAB编程计算出上证180指数的日收益率,然后作出其日收益率的时间序列图和直方图(图略)。上证180指数收益率序列的基本统计特征如下表所示:
从上表关于上证180指数收益率序列的基本统计特征值中可以得出,上证180指数不符合正态分布的要求,其JB统计量大大超出了临界值。同时,其偏度小于零,即向左偏移,峰度大于正态分布峰度值3,即具有肥尾现象。以上表中所得出的结论,我们可以从上证180指数的收益率时间序列图和直方图中得到很好的论证:我国股票市场收益率序列存在明显的波动聚集和尖峰、肥尾现象,传统的基于正态分布假设的静态模型不足以扑捉金融时间序列这一特性。因此,我们选择基于GARCH模型的CVaR方法动态模型来分析其波动特性和条件风险价值。
为了便于计算,对于波动性建模,我们采用GARCH(1,1),即:

利用极大似然值法,对(8)式进行参数估计,可以得到条件序列与μ值。 算出了σt的值,我们将其带入(12)式,便可以求得正态分布下传统风险价值VaR的大小。同时,由(13)式可知,利用极大似然值法进行参数估计后,得到的条件序列与μ值一起带入下式:


Model GARCH(1,1)-N-VaR GARCH(1,1)-t-CVaR最小值0.0015 0.0021最大值0.075 0.084平均值0.036 0.067标准差0.0087 0.015失败天数28 9失败率0.065 0.028
从上表可以看出,由GARCH(1,1)-t-CVaR计算所得平均值在大于GARCH(1,1)-N-VaR的平均值,同时由GARCH(1,1)-N-VaR模型计算所得失败率0.065大于失败率期望值说明该模型计算所得风险低估了实际风险大小。因此,与传统的基于正态分布假设计算的风险价值VaR相比,基于GARCH模型的学生t分布所计算的条件风险价值能够更加客观、真实地度量信用风险大小。
3 结论
本文主要介绍了VaR和CVaR的一些基本概念和计算方法,在VaR基础上衍生出来的CVaR模型,不仅继承了传统VaR风险测定模型的优点,更重要的是它对尾部风险进行了定量描述,通过尾部风险求平均的原理,对风险的预测更准确、保守,符合风险管理谨慎的原则。同时具有连续性、一次可加性、正均性、凸性、一次单调,二次递增等良好的数学特性。针对许多金融时间序列模型,其收益率分布所表现出的“尖峰”“厚尾”等特性,而简单的对数正态分布,学生t分布对其特性无法捕获。本文提出GARCH模型,并通过实证分析,说明该模型能较好地处理异方差问题,并能有效地消除收益率分布的尖峰厚尾性影响。在研究的过程中,笔者也发现一些疑点和今后有待进一步解决的问题。首先GARCH模型测度金融风险收益率时,对系数参数的非负性约束太强,过度的限制了条件反常的动态性;其次,用CVaR进行风险测度时,笔者只着眼于计算既定置信水平下在持有期末这一时刻的风险,而忽略了这一持有期内收益率剧烈波动所带来的风险,没有考虑用连续的CVaR方法度量风险。
[1]Basle Committee on Banking Supervision.An Internal Model-Based Approach to Market Risk Capital Requirements[C].Basle Committee on Banking Supervision,1995.
[2]Rockafeller T,Uryasev S.Conditional Value-at-Risk for General loss Distributions[J].Journal of Banking and Finance,2002,26(7).
[3]Artzner P,Dellbaen F,Eber J M,et al.Coherent Measures of risk[J].Mathematical Finance,1999,9(3).
[4]蔡瑞胸(Ruey S.Tsay).金融时间序列分析[M].潘家柱译.北京:机械工业出版社,2006.
[5]李坤.VaR与CVaR在金融风险测度中的应用[D].青岛大学硕士学位论文,2006.
[6]王玉玲.CVaR方法在投资组合中的应用[J].统计与决策,2008,(2).
[7]温红梅,姚凤阁.CVaR在操作风险度量与控制中的应用分析[J].哈尔滨商业大学学报,2008,(1).
[8]杜红军.VaR和CVaR风险值的估计和计算[D].华中科技大学硕士学位论文,2006.
[9]迟国泰,王际科等.基于CVaR风险度量和VaR风险控制的贷款组合优化模型[J].预测,2009,(2).

