金融时间序列间的条件相关性分析与Copula函数的选择原则
李述山
(山东科技大学 信息与工程学院,山东 青岛 266510)
0 引言
Copula函数是连接随机变量边缘分布的连接函数,Sklar指出对于一个具有边缘分布F1,F2,…,Fm的联合分布函数F,一定存在一个 Copula 函数 C,使得 F(x1,…,xm)=C(F1(x1),…,Fm(xm))。事实上,Copula函数描述了变量间的相关结构,运用Copula技术来分析随机变量间的相关性有很多优点:与线性相关系数相比,由Copula函数导出的一致性和相关性测度可以捕捉变量间非线性相关关系,因此应用范围更广、实用性更强;与基于联合分布函数的建模方法相比,Copula模型更为灵活。这表现在如下两个方面:一是Copula模型不限制边缘分布的选择,而且Copula函数有很多分布族;二是Copula模型将随机变量之间的相关程度和相关模式有机地结合在一起,不仅可以得到度量相关程度的相关参数,还可以得到描述相关模式的Copula函数,可以更全面地刻画随机变量间的相关关系[1]。因此,Copula技术在相关性分析及风险分析等方面得到了广泛的应用。
当我们用Copula函数来刻画条件联合分布时,就可以进行条件相关性分析。本文拟建立条件相关性的概念以及条件相关性度量,提出相关性分析中Copula函数选择的原则,通过构建Copula-EGARCH模型,将两个金融资产间的条件相关性转化为标准化残差间的相关性进行分析,并进行实证研究。
1 相关性度量与条件相关性度量
1.1 相关性度量
传统的线性相关系数已经不适应金融风险分析的需要,Kentalτ、α 上尾相关系数 λL(α)、下尾相关系数 λU、上尾相关系数λL、下尾相关系数已成为几种最重要的非线性相关系数,它们在金融风险分析中具有重要的作用,且都可以由Copula进行表达[1~4]:
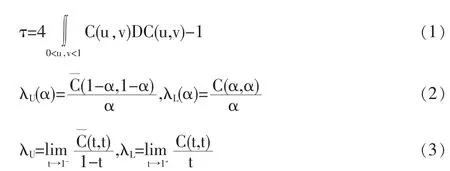
1.2 金融时间序列间的条件相关性度量
对两金融时间序列{Xt,t=1,2,…,n},{Yt,t=1,2,…,n},记Ψt为t及其以前时刻的信息集,我们关心的是在Ψt-1已知的条件下,Xt与Yt的相关程度。
定义1 称在Ψt-1已知的条件下,Xt与Yt之间的相关性为Xt与Yt的条件相关性。
定义2 设在Ψt-1已知的条件下,Xt与Yt的联合分布函数为 Ht(x,y),边际分布函数分别为 Ft(x),Gt(y),则存在一个Copula 函数 Ct使得 Ht(x,y)=Ct(Ft(x),Gt(y)),称 Ct为(Xt,Yt)在Ψt-1已知条件下的条件Copula函数。
类似于非条件相关性度量,我们定义相应的条件相关性度量。条件τ:τC,条件α上尾相关系数条件 α 下尾相关系数:条件上尾相关系数条件下尾相关系数:同样它们可以由相应的条件Copula函数进行表达。
定义3 设{Xt},{Yt}为两个随机变量序列,定义在Ψ(t-1)已知条件下Xt与Yt之间的条件Kendall相关系数为:
τC=P{(Z1t-Z2t)(W1t-W2t)>0}-P{Z1t-Z2t)(W1t-W2t)<0}
其中(Z1t,W1t)和(Z2t,W2t)独立且与(Xt,Yt)|Ψ(t-1)同分布。
τC度量了Xt与Yt在Ψ(t-1)已知的条件之下变化的一致性程度。
定义 4 设 {Xt},{Yt} 为两个随机变量序列,(Zt,Wt)=(Xt,Yt)|Ψ(t-1)的联合分布函数为Ht(x,y),边际分布函数分别为Ft(x),Gt(y),则 Xt与 Yt在 Ψ(t-1)已知条件下的条件 α 左尾相关系数和条件α右尾条件相关系数分别定义为:
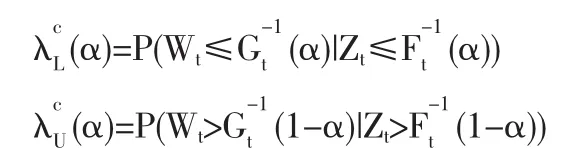
左尾相关系数和右尾条件相关系数分别定义为:

结论:设(Zt,Wt)=(Xt,Yt)|Ψ(t-1)对应的 Copula 函数为 Ct,则

2 相关性分析中Copula函数的选择原则
采用Copula技术进行相关性分析,就要求Copula函数要很好地刻画各种非线性相关关系,这体现在两个方面:一是Copula函数要能很好地拟合实际数据;二是Copula函数要能够充分反映各变量间的非线性相关性指标。因此我们提出如下选取原则。
2.1 Copula函数与经验Copula函数的拟合程度要高
首先,所选择Copula函数要通过拟合优度检验,如K-S检验、χ2拟合优度检验等。文[9]引入了一个评价Copula函数的χ2拟合优度的拟合优度检验法(以二元情况为例):设(U,V)为边缘分布均为[0,1]上均匀分布的随机向量,(uk,vk)(k=1,2,…,n)为样本,将[0,1]均匀分割成 m×m 个单元格 G(i,j)(i,j=1,2,…,m)记 Aij为落入单元格 G(i,j)内的实际频数,Bij表示落入单元格G(i,j)内的理论频数,则在原假设H0:(U,V)~C(u,v)成立时

渐进服从自由度为m2-1的χ2分布。在实际应用中,观测点个数过少的单元格通常可以合并,若需要估计的未知参数个数为p,合并的单元格数为q,那么自由度将减少到m2-p-q-1。
其次,在通过拟合优度检验检验的条件下,拟合程度越高越好。记C(u,v)与C~(u,v)分别为Copula函数及相应的经验Copula函数,则的大小刻画了 Copula函数对数据的拟合程度,Wn的取值越小,拟合程度越高。
2.2 能够较全面地刻画非线性相关性
Kendall的τ、α上尾相关系数与α下尾相关系数等是重要的相关性指标,Copula函数的选择要较好地反映这些相关性指标。
(1)Kental的 τ:设(ξ,η)为二维随机向量,基于(ξi,ηi)(i=1,2,…,n)((ξi,ηi)为(ξ,η)的样本)的 τ的非参数估计量为[1]:
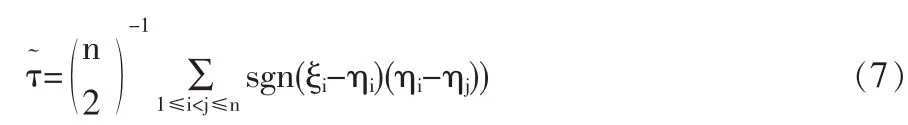
(2)α上尾相关系数与α下尾相关系数
记 C(u,v)为(ξ,η)对应的 Copula 函数,(u,v)是相应的经验 Copula 函数,由于(u,v)是 C(u,v)的估计量,因此,我们用如下二式作为α上、下尾相关系数的非参数估计:

即用参数估计法得到的Kendall的τ、α上、下尾相关系数的估计要与上述非参数估计接近。
上述原则对条件Copula函数的选择同样适用。
3 基于Copula-EGARCH模型的条件相关性分析
假设X1t,X2t为t时刻两项资产(或资产组合)的对数收益率,用Copula-EGARCH模型刻画:
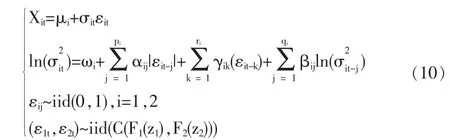
引理[2]连接函数对于随机变量的严格单调增变换是不变的。
由式(10)可以看出,在t-1时刻的信息集Ψt-1给定的条件下,Xt=(X1t,X2t)是 εt=(ε1t,ε2t)的严格增变换,因此有如下推论。
推论 收益率向量Xt=(X1t,X2t)在Ψt-1已知条件下的条件 Copula 函 数 与 标 准 化 残 差 εt=(ε1t,ε2t) 的 Copula 函 数 相同,因此X1t与X2t之间的条件相关性与ε1t,ε2t之间的相关性相同。
由推论可以看出,X1t与X2t之间的条件相关性可以通过残差 ε1t,ε2t之间的相关性获得。 由于 εt=(ε1t,ε2t)(t=1,2,…,T)独立同分布,可以视为来自同一个二维总体的样本,因此ε1t,ε2t之间是常相关的,从而X1t与X2t之间的条件相关性是常相关的,其相关性参数可以用通常的参数估计法进行估计。
4 实证分析
本文采用上证综指与深证成指数据,利用4种常用的Archimedean Copula[3~6]:Gumble Copula、Clayton Copula、GSCopula和BB1 Copula进行实证研究 (Frank Copula不能捕捉尾部相关性,故不采用),其中GS Copula与BB1 Copula的分布函数的表达式分别为:
CGS(u,v,θ)=[1+((u-1-1)θ+(v-1-1)θ)-1/θ]-1(θ≥-1,θ≠0)
CBB1(u,v,θ,δ)={1+[(u-δ-1)θ+(v-δ-1)θ)1/θ}-1/δ(θ≥-1,θ≠0,δ>0)
4.1 样本选取与参数估计
本文采用的样本数据为2000年1月4日至2008年6月27日的上证综指与深证成指的收盘价pit(i=1,2),总样本数为2009,以对数收益率为研究对象,对数收益率{rit}定义为:rit=100(lnpit-lnpit-1),共2008对日收益率数据。
基于金融序列的尖峰厚尾特性,我们采用GED分布对EGARCH模型建模,用Eviews软件对EGARCH模型(10)参数进行估计,通过编程对误差分布进行K-S检验,参数估计与检验统计量Dn的结果见表1。
利用如上4种Archimedean Copula函数对二残差序列进行拟合,通过Matlab编程得到Copula参数的极大似然估计,将[0,1]2均匀分成6×6的单元格进行χ2拟合优度检验,得统计量M(自由度),计算Wn的值,结果见表2。
表1说明两个序列用EGARCH模型拟合具有良好的效果。表2表明在水平0.05下只有GS-Copula与BB1 Copula能够通过χ2拟合优度检验,且BB1 Copula拟合效果最好。
4.2 Copula函数的确定与相关性分析

表1 模型参数估计结果与K-S检验统计量Dn值
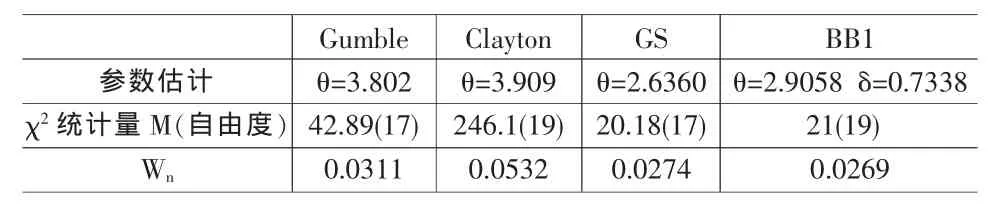
表2 Copula的参数估计值、及χ2拟合优度检验统计量M(自由度)的值以及Dn值
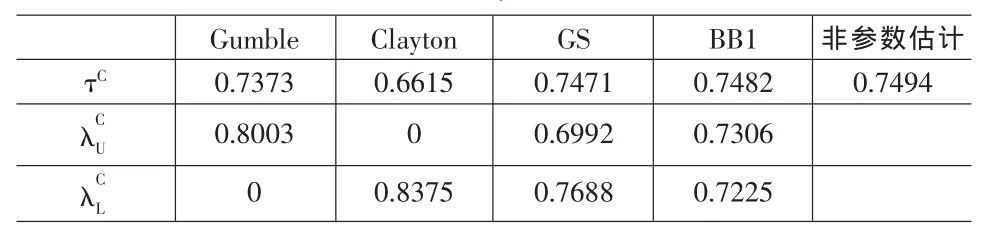
表3 τ、λU、λL的 Copula 估计值
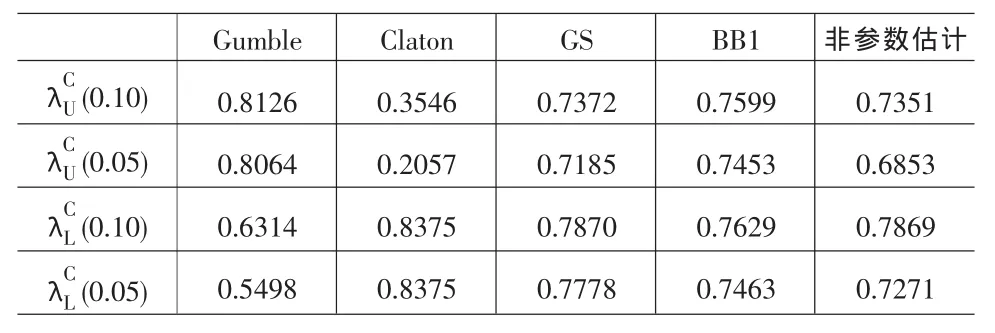
表4 α条件上尾相关系数与α条件下尾相关系数估值
一方面,从表3及表4可以看出,4种Copula中只有GS Copula与BB1 Copula能够较全面地反映α条件上尾相关性、α条件下尾相关性以及条件τ,因此,只有GS Copula与BB1 Copula能较好地反映上证综指与深证成指之间的条件相关性。
另一方面,由GS-Copula与BB1-Copula得到的相关性指标可以看出,上证综指与深证成指之间具有很强的条件相关性,条件接近0.75,条件τ上尾相关系数、条件下尾相关系数都在0.7以上。
5 结论与分析
本文类似于通常的非线性相关性度量,建立了条件τ等几个条件相关性度量,提出了相关性分析中Copula函数选择的两个原则,通过构建Copula-EGARCH模型,将两个金融资产间的条件相关性转化为标准化残差间的相关性进行分析,对上证综指与深证成指数据进行实证研究,发现在常见的几种Archimedean Copula中GS-Copula与BB1 Copula对金融市场相关性的描述具有良好的效果,能够较全面地反映两个市场之间各种非线性相关性,并且沪市与深市之间的条件相关性很强。同时,通过GS-Copula与BB1 Copula得到的相关性指标可以看出:沪市与深市之间具有很强的条件相关性,并且在下跌时条件相关性更强。这说明如下三个问题:第一,两市具有共同的外部影响因素,如重大的利好或利空消息或其它市场的信息会对两市制造类似的影响,即市场的外部驱动是类似的;第二,身在沪市的投资者密切关注着深市的市场变化,反之亦然;第三,投资者对其它市场的变化相当敏感,对其它市场下行变化更加敏感。
[1]Nelsen R B.An Introduction to Copulas[M].New York:Springer,1998.
[2]张尧庭.连接函数(Copula)技术与金融风险分析[J].统计研究,2002,(4).
[3]郭惠,罗俊鹏,史道济.半参数阿基米德Copula的理论应用[J].天津理工大学学报,2007,23(5).
[4]李悦,程希骏.上证指数和恒生指数的Copula尾部相关性分析[J].系统工程,2006,149.
[5]李秀敏,刘敏星,刘金宪.基于Copula的金融资产相关结构建模[J].数学的实践与认识,2007,37(18).
[6]王璐,王沁,庞皓.股票收益率尾部相关性的Copula度量及模拟[J].数学的实践与认识,2007,37(10).
[7]韦艳华,张世英.金融市场的相关性分析—Copula-GARCH模型及其应用[J].系统工程,2004,22(4).
[8]Frees E W,Valdez E A.UnderstandingRelationshipsUsing Copulas[J].North American Actuarial Journal,1998,2(1).
[9]Genest C,Rivest L.Statistical Inference Procedures for Bivariate Archimedean Copulas[J].Journal of the American Statistical Association,1993,88.
——拟合优度检验与SAS实现

