均匀分布和密度与正态密度的逼近速度及应用

李瑞阁，万冰蓉，许洪范

(1.南阳理工学院应用数学系,河南 南阳 473006；2.南昌工程学院 理学系,南昌 330099)

1 IID均匀分布和密度函数一般公式及期望方差公式

（1）设 X1，X2，…，Xniid～U（0，1）当 x∈[k，k+1]时，

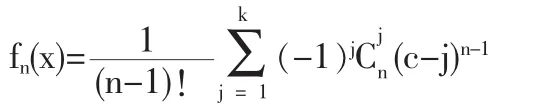
对于其他x上式等于0。

2 IID均匀分布和密度与正态密度拟合图,两者差的绝对值图，绝对值最大值表及趋势图

（1）在数学上，数形结合的思想，不仅能从直觉上给我们以启示,常常能借助变化的趋势，发现事物的客观规律性。

用正态分布去拟合fn(x)主要有两种方法：

②用曲线拟合最小二乘法，用数学软件编程实现:如n=5,N(2.5,0.4489)。

这里用第二种方法。用Matlab分别画出当n=2，3，4，5时的和分布密度图及相应的正态分布图 （见图1，图2，图 3，图 4）。

③用Matlab分别画出当n=2，3，4，5时的相应和分布密度与正态密度的差的绝对值在 [0，3]，[0，5]，[0，6]，[0，8]内，依次取 100，100，150，200 个等分点的差值图（见图 5，图 6，图 7，图 8），并计算出对区间尽可能细分情况下，和密度函数与相应正态分布函数的差的绝对值的最大值。

其中，当 x∈[k,k+1]时，

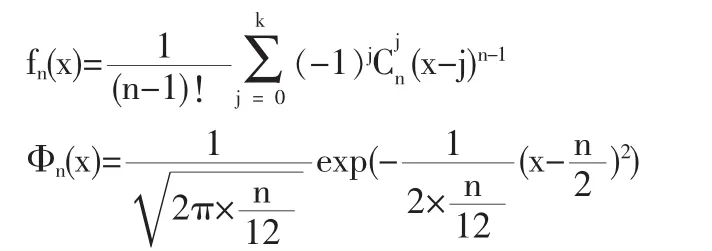
当 n=2,3,…，31 时，an在[0,n+2]上的最大值（见表 1），并画出前24个值对应的差的绝对值最大值趋势图（见图9）。

3 正态分布拟合结论

(1)由图1，图2，图3，图4可观察到:随着服从均匀分布的多个独立随机变量个数n不断增大，这些变量和的密度函数与对应的正态分布的拟合程度愈来愈好。

(2)由图5，图6，图7，图8观察发现,和密度函数与正态分布密度函数差的绝对值最大值，分别在和密度函数不为零的区间[0，2]，[0，3]，[0，4]，[0，5]上达到，且从右端点开始，在扩大的区间[0，3]，[0，5]，[0，6]，[0，8]上，随着自变量的增大，差的绝对值越来越小，这个趋势可随区间的继续增大而无限趋近于0；同理，由正态分布的对称性，在左端点以外，和密度函数为零区间上，可以预见，随着自变量的减小，差的绝对值越来越小,无限趋近于0。

(3)由图9，表1很清楚的看到随着变量个数的增加，分段函数在放大区间上，和密度函数与正态密度函数的差绝对值的最大值，随着n增大，逐渐减小，越来越趋近于零，分布密度与正态分布密度随着n的增大，逼近速度越来越快。

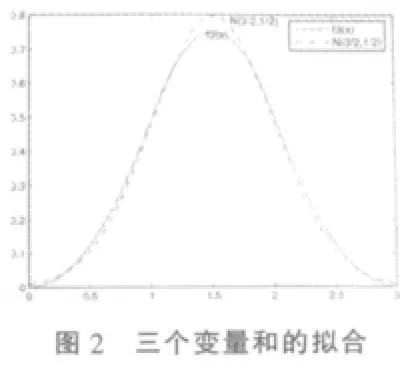
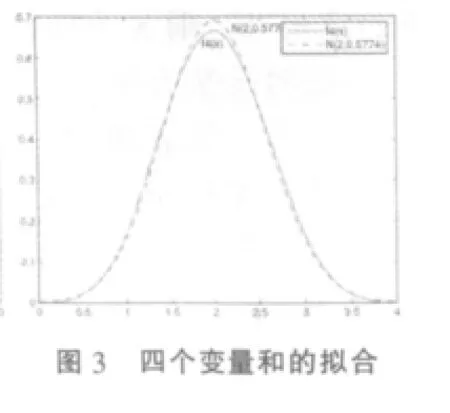
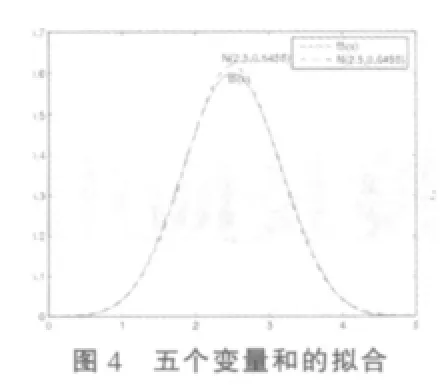
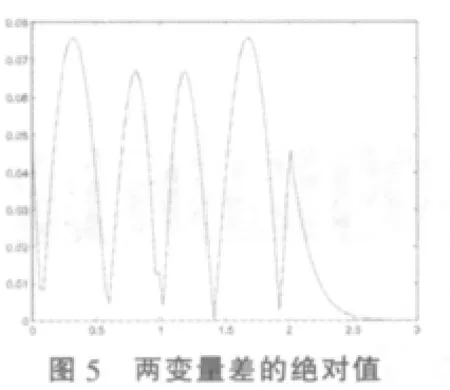
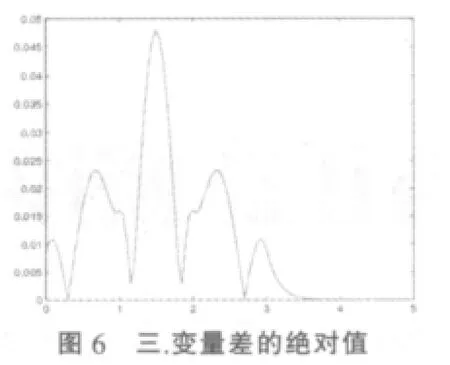
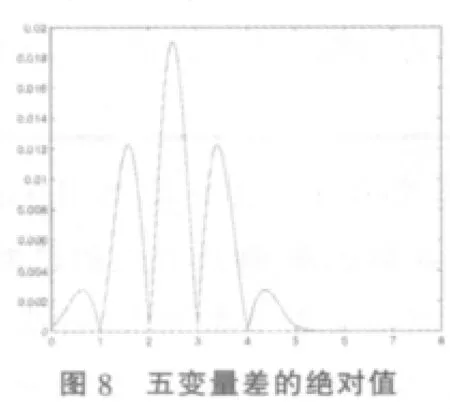
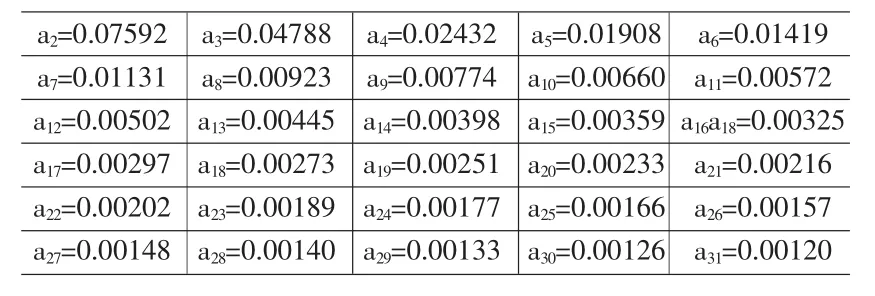
表1 差绝对值的最大值数据

(4)利用Matlab考察和密度函数与正态分布密度函数差绝对值的最大值an随n的变化趋势。利用逐步回归法，并根据常识确定an与及n-1的关系为

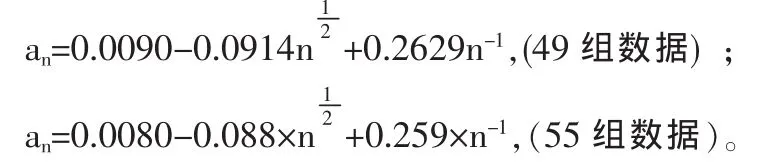
复相关系数R为0.997，且以此方程预测an的值与实际值差趋近于0，因此认为该方程适合统计学理论Edgeworth展开理论。不仅有统计学意义，且有实际意义。当n→∞，an→0。

综上，当服从均匀分布的独立随机变量个数很多时，均匀分布和分布无限逼近正态分布，它们和的分布可近似看成正态分布，这个结论符合中心极限定理。

4 和分布密度逼近正态分布密度函数的结论,用于正态随机数生成

由于上述的特性以及下面理论上的原因，均匀分布U(0,1)在随机模拟中起着特殊的作用。通过产生大量相互独立的U(0,1)的随机数，经过一些相应的变换可得到其他形式(正态分布、指数分布、Gamma分布等)的随机数。

命题1:若随机变量Y有严格单调上升连续的分布函数F(y)，X=F(Y)，则 X 为随机变量。

证明:∵Y为随机变量，

∴∃一维β集，及σ代数F,使得 Y-1(-∞,w)∈F

∴对于一维 β 集(-∞,η)有

X-1((-∞,η))=(F(Y))-1(-∞,η)=Y-1(F-1(-∞,η))∈F (F-1(-∞,η)∈β)

∴X为随机变量。

命题2 若随机变量Y有严格单调上升连续的分布函数 F(y)，X=F(Y)则 X～U（0，1）， 反 之 ,若 Z～U（0，1）,F为任一严格单调上升连续的分布函数，F-1为它的反函数，则 W=F-1（Z）的分布函数为 F（w）。

表2 均匀分布随机数

证明:对任一 0≤x≤1有

P(X≤x)=P(F(Y)≤x)=P(Y≤F-1(x))=F(F-1(x))=x

∴X～U(0,1)

反之，若Z～(0，1)，F为任一严格单调上升连续的分布函数，F-1为它的反函数，则W=F-1(Z)的分布函数为F(w)。

P(W≤w)=P(F-1(Z)≤w)=P(Z≤F(w))=F(w)

∴W的分布函数为F(w)。

利用上述关系，可以产生各种常见分布F(x)的随机数。所谓某个分布F(x)的随机数，是指从分布F(x)的总体中随机地抽取一个大样本的数值，借助适当运算得到。

用机器来模拟抽样比实际抽样不仅成本低，而且可以有效地防止一些不必要的干扰，从而广泛地应用于各个领域中。

5 产生正态随机数的方法

在(0，1)中产生n个均匀分布的随机数X1,X2,…，Xn即设X1,X2,…，Xn独立同分布，由于

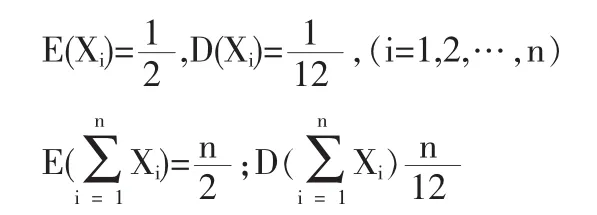
由中心极限定理知

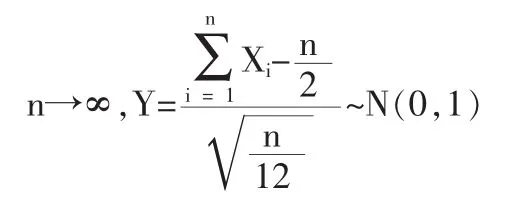
故Y为所求的N（0，1）的随机数。

例：今用Matlab软件,取得的均匀分布随机数（见表2）。进而计算正态随机数为

[1]李瑞阁,黄尧.服从均匀分布的多个独立随机变量和的密度函数公式[J].南阳师范学院学报,2007,(6)3.

[2]梁之舜,邓集贤,杨维权等.中山大学数学系.概率论及数理统计[M].北京:高等教育出版社,2003.

[3]沈鸿.一类U统计量函数的Edgeworth展开[J].中国计量学院学报,2005,16(2).

[4]高惠璇.统计计算[M].北京:北京大学出版社,2005.[5]方开泰等.统计分布[M].北京:科学出版社,1987.