三维随机变量和谐指标与二维边缘和谐指标的关系探讨
张明珠,岳晓鹏,田 萍
(许昌学院 数学科学学院,许昌 461000)
0 引言
在概率中总是假定随机变量之间是相互独立的,但在很多实际问题中独立很难满足,随机变量之间存在着千丝万缕的联系。因此对随机变量的这种复杂关系,即相依性的研究一直以来是个热点问题[1,2],对它出现了很多不同指标的刻画,Kendall’s τ[3]就是其中的一个,它刻画出了二维随机变量,对于二维以上的随机变量却没有定义。因此本文拟建立三维随机变量的和谐定义,即从和谐的角度衡量了三维随机变量之间的相依关系。借助于连接函数copula得到其计算公式,并且进一步讨论得到几个等价的计算公式。最后讨论三维随机变量和谐度量指标和二维边缘和谐度量指标的关系,得到它们之间关系的表达式。本文第一部分将介绍copula[3]函数和Kendall’s τ的定义及相关结论;第二部分将建立三维随机变量的和谐定义,并借助copula函数得到其计算公式;第三部分将具体讨论三维随机变量的 Kendall’s τ与二维边缘Kendall’s τ的关系。
1 Copula函数和二维随机变量的和谐指标
布,则二维随机变量的Kendall’s τ的定义为
τ=τX,Y=P((X1-X2)(Y1-Y2)>0)-P((X1-X2)(Y1-Y2)<0)
为了方便研究,这里把二维随机变量的和谐度量指标Kendall’s τ简记为 τ(2)或 τ(2)X,Y。
引理1[3]条件同上,若二维随机变量是连续型的,存在唯一的 Copula 有 H(x,y)=C(F(x),G(y)),则

通过τ的定义可以看出,它从一个侧面反映了二维随机变量X和Y的相依关系。就是用二维随机变量(X,Y)是一致增或一致减与非一致增或非一致减的差值来表现的它们之间的相依性,是衡量复杂的相依关系的一个度量。其实它是一种序的关系。这里把随机变量之间的一致增和一致减统称为一致序,把随机变量之间的一增一减统称为不一致序。当然也可通过τ(2)值反映出随机变量取值的一种变化。因此成为衡量相依关系的一个重要指标。
三维随机变量的相依性将更加复杂,下面就从和谐的角度给出相依性的一种度量,因为这种定义和二维的几何意义相同,所以也把它命名为和谐指标。
Copula是连接联合分布函数与其边缘分布函数的函数(有的文献把它称为连接函数[2])。下面给出Copula的存在性定理。即Sklar定理[3]。
Sklar定理[3]令二维随机变量(X,Y)的联合分布函数为H,边缘分布函数分别为F和G,那么存在一个Copula,有
H(x,y)=C(F(x),G(y)),∀(x,y)∈R2
若F和G连续,则C是存在唯一的。相反,如果C是Copula,并且F和G是分布函数,则由上式确定的H是边缘分布分别为F和G的联合分布。
下面给出二维随机变量的Kendall’s τ的定义[3]。
定义1[3]设二维随机变量(X1,Y1)和(X2,Y2)服从同一分
2 三维和谐度量指标Kendall’s
定义2 设三维随机变量(X1,Y1,Z1)和(X2,Y2,Z2)具有相同的联合分布函数H(x,y,z),三维随机变量和谐指标的定义为

为了和二维和谐度量指标Kendall’s τ区别,记三维和谐度量指标 Kendall’s τ为或 τ(3)X,Y,Z。
因为[P(X1-X2)(Y1-Y2)(Z1-Z2)>0+P(X1-X2)(Y1-Y2)(Z1-Z2)<0]=1,所以定义2可以简化为

从定义2可以看出,三维和谐度量指标Kendall’s τ是一致序减去不一致序,它与二维的定义的几何意义是相同的。由于和谐度量指标Kendall’s τ一般是衡量二维随机变量之间序关系的度量,对三维随机变量没有具体的刻画,而τ(3)也是从序的角度衡量随机变量之间关系的度量,因此可以说三维和谐度量指标 Kendall’s τ是二维和谐度量指标Kendall’s τ的一种推广。
三维随机变量的和谐指标τ(3)同样可以借助于Copula这个工具来表达。
定理1 设(X1,Y1,Z1)和(X2,Y2,Z2)是两个同分布的三维连续型随机变量,且联合分布函数为H,边际分布分别为F1(x),F2(x)和 F3(x)。 令 C 为三维随机变量的联合分布对应的Copula,有 H(x,y,z)=C(F1(x),F2(x),F3(x)),则

证明:首先

类似的

所以

结论得证。
由定理1的结论知,三维Kendall’s τ也可以完全借助Copula表达。三维Kendall’s τ还有另外一种Copula表述形式,如下定理所示:
定理2 前提条件同定理2,则

对 P(X1<X2,Y1<Y2,Z1<Z2)的证明换一种角度
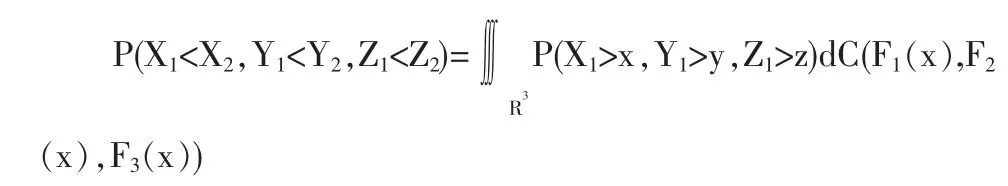
因为

又因为


因此

所以

结论得证。
通过定理1和2的证明可知,τ(3)的两种Copula形式是等价的。定理2的结论更适合当Copula C是对称形式时的使用。当然也可以根据不同的情况,采用不同的形式。通过上述两个定理的证明,可以得到一个有趣的结论。
结论1 设(X,Y,Z)为任意的三维连续随机变量,且联合分布函数为 H,边际分布分别为 F1(x),F2(x)和 F3(x)。 令 C为三维随机变量的联合分布函数对应的Copula,即H(x,y,z)=C(F1(x),F2(x)和 F3(x))。 则

证明:只需利用定理1和2的结论即可得上式。
三维 Kendall’s τ和二维 Kendall’s τ具有一定的联系,又有一定的差别。那么能否建立三维Kendall’s τ与其自身的二维边缘Kendall’s τ的关系呢?下面来研究它们之间具有何种关系。
3 三维和谐度量指标Kendall’s与二维边缘Kendall’s 的关系
定理3 设(X,Y,Z)为三维连续的随机变量,联合分布函数为 H,一维边缘分布函数分别 F1(x),F2(y)和 F3(x)。令分布函数对应的 Copula 是 C,有 H(x,y,z)=C(F1(x),F2(y),F3(x))则

其中 τ(2)X,Y、τ(2)Y,Z、τ(2)X,Z分别表示随机变量(X,Y,Z)的二维随机变量(X,Y)、(Y,Z)、(X,Z)的二维边缘 Kendall’s τ。
证明:由随机变量(X,Y,Z)和(X,Y)的关系知,随机变量(X,Y)的联合分布函数为 H(x,y,+∞),则联合分布函数对应的 Copula 为 C(F1(x),F2(y),1)。 由二维 Kendall’s 的定义知,随机变量(X,Y),(X,Z)和(Y,Z)的 Kendall’s τ分别为

τ(2)X,Y、τ(2)Y,Z、τ(2)X,Z分别是 二 元函数的 积 分表达式 ,因此若想建立 τ(3)和它们的关系,就必须想办法使 τ(3)这个三重积分表达式变为二重积分表达式。记
Δai=C(u1,u2,ai)-C(u1,u2,ai-1) (i=1,2,…,n)
令 λ=max{Δa1,Δa2,…,Δan},则

同理

所以由定理2得


结论得证。
由定理 3可得到三维 Kendall’s τ与二维边缘 Kendall’s τ的关系。从而说明,三维Kendall’s τ可以通过它的分量,即二维边缘Kendall’s来表示,二者之间存在密切的关系。定理4还给出了求三维Kendall’s τ的另一种方法,即可以借助二维边缘 Kendall’s τ来求 τ(3)。
例 1:设三维连续的随机变量(X,Y,Z)对应的 Copula[2]形式如下,求 τ(3)。

解:(方法 1)首先利用定理 2 求 τ(3)。

由Copula的对称性知

(方法 2)由定理 3知,只需要求出二维边缘 Kendall’s τ即可求得 τ3。

4 结束语
本文从和谐的关系出发度量和刻画了三维随机变量之间复杂的相依关系,对解决实际问题提供帮助。并且进一步探讨三维随机变量的和谐指标 Kendall’s τ与二维边缘Kendall’s τ之间的关系,还建立了它们之间关系的恒等式。这在二维的和谐关系的研究基础之上又前进了一步,具有较强的理论意义。在今后的研究中,将对它们之间关系作更深入的挖掘。
[1]张尧庭.我们应该选用什么样的相关性指标[J].统计研究,2002,(9).
[2]Roger.B.Nelsen.Multidimensional Dependency Measures[J].Journal of Multivariate Analysis,2004,89.
[3]Roger.B.Nelsen.An Introduction to Copulas[M].New York:Springer-Verlag,Inc,1999.

