过程调整方法的效应分析

张 黎

（郑州航空工业管理学院，郑州 450015）

0 引言

如何对制造过程质量进行有效的监控，一直是质量控制理论和生产实践中的难题。在离散零件制造行业，传统的质量工程师更熟悉应用统计过程控制(SPC）方法对过程进行监控。然而，进入20世纪90年代，制造环境发生了变化[1，2]，主要表现为：（1）制造过程数据自相关；（2）短期小批量制造导致对制造设备的频繁调整，增加了过程初始误差。这些问题如果仍然只使用SPC的控制图技术对过程进行监控，已经变得毫无意义，尤其在过程自相关或系统误差较小时，停工检修并不可行。对环境(1)，可以引入工程过程控制（EPC）方法对过程实施调整，消除过程的自相关，然后采用SPC进行监控。这种把SPC监测与EPC调整的整合模式,作为20世纪90年代最重要的质量控制的创新，较好地解决了现代制造过程的质量监控问题，受到理论界和实务界的广泛关注[3，4]。由于通常所说的过程调整方法主要是指EPC方法[5]，其调整的原理是利用可控的输入变量补偿过程输出误差，使输出围绕目标值波动。然而，在SPC领域，传统上由于受到戴明漏斗实验的影响，避免在制造中调整过程，通常在发现由特殊原因引起的波动后，要停机检查。但在环境（2）下，如果过程均值不受过程波动的影响，可以采用Grubbs调和规则[6]对初识误差进行调整。这里所谓的“调整”，与EPC不同，主要是修正或消除由特殊原因引起的异常波动，使得输出均值恢复到受控的水平，在SPC的假设下，Grubbs调和规则是一种可行的方法，但并未引起重视和应用。因此，本文通过对Gbuss调整和EPC的最小均方误差（MMSE）调整的效应分析，比较两种调整方法的特点，充分肯定过程调整在现代制造环境下的必要性，以期为进一步深化对过程调整方法的研究提供参考,有助于在实践中更好地推行和实施。

1 过程调整的必要性

传统上，制造过程大多处于统计稳态，即过程围绕目标值的随机波动由正常原因引起，这样，人们担心一旦采取调整行动将会加大过程的波动。用戴明的话说[7]：“不要干预这个过程”。

考虑戴明的漏斗实验规则1和规则2，设过程模型为：

Yt=αt+Xt-1,Xt=Xt-1+μt

假设初始漏斗瞄准在目标值上，X0=0，Yt表示在时刻t的观测值（落点位置），随机误差α1的均值为零、方差为μt=Xt-Xt-1为调整量，Xt为可控因素的水平（漏斗的位置），目标值为M=0。

规则1：开始漏斗瞄准目标值，每次都不调整瞄准的位置。 调整量 μt=Xt-Xt-1=0，因此，Xt=M=0；Yt=αt，这意味着没有调整，过程处于统计稳态，

规则2：根据上一次落点的位置与目标值的差距调整漏斗，以当前的位置为基准。 μ0=0；μt=Xt-Xt-1=-Yt；Yt=αt-αt-1。 因此，过程为一阶移动平均MA(1)模型，过程表现为平稳的时间序列，方差增加了一倍，即规则2表示，只要对处于统计稳态的过程进行调整，方差就会增加，即Var(Yt)＞2σα2。正是基于戴明的规则2，在传统的SPC领域，调整成为大忌。

然而，我们应该关心的问题是：假如对于统计稳态过程，我们引入一个调整方法进行了调整，过程的波动到底增加多少呢？比如，采用指数加权移动平均（EWMA）调整，取平滑常数λ=0.2，则调整后的方差是调整前的1.11倍；若平滑常数λ=0.4，则调整后的方差是调整前的1.25倍。事实上，EWMA调整类似于规则 2，这里的调整量，即部分调整代替了规则2的全部调整ut=-Yt。因此，调整的风险并不是很大，真正的风险是该调整时而没有调整[8]。

值得研究的问题是在小批量生产过程中，机器的初始设置使得过程输出偏离目标值，这样，过程围绕这个偏离的目标值处于统计稳态。如果根据规则1，不进行调整，过程输出如图1中的上部，偏离了目标值。如果采用规则2调整1次，则过程输出如图1中的虚线。第三种调整是使用Grubbs调和序列连续调整5次，则过程输出如图1中的黑点连线。从图1中比较可以看出，调整使得过程接近目标值。

不少文献指出[9～12]，只采用控制图监控过程，即使做出最大的努力，过程均值仍然会有漂移。统计稳态并不是经常存在的，过程数据大多表现为自相关（包括非平稳的情况），此时，调整被证明是有益的，调整可以减少过程的波动。例如，设过程为Yt=αt+μt，这里的μt是过程均值，这个均值可以是一个随机漫步，也可以是一个平稳过程，如果不对其调整，过程将偏离目标值。对于随机序列的情况，我们可以使用MMSE调整，本质上也是规则2的实现。因为，自相关的存在可以对下一个观测值做出预测，如果影响过程的可控因素已知，对可控因素的调整就可以修正下一个观测值对目标值的偏移。因此，除了理想的统计稳态的情况，调整是必要的，特别是在过程均值具有趋势漂移时。

2 MMSE调整方法

2.1 AR（2）过程的MMSE调整方程

在大部分零件制造过程，一个合理的假定是过程调整的所有效应在下一时间期全部实现。设过程目标值为零，这样，调整后的输出误差为

这里，过程可控输入变量为Xt，设过程干扰模型为AR(2)，即

Zt的一步提前预测为

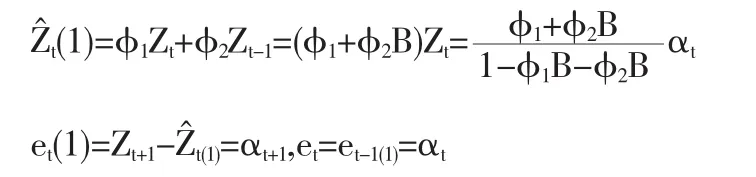
MMSE控制的目的是为了使输出误差达到最小，故令

即为 MMSE 调整方程。 把式（2）、（3）代入式（1）得

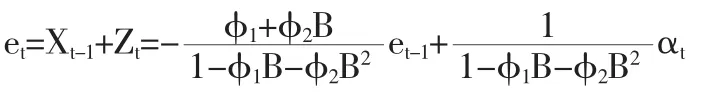
即 et=αt，方差

因此，对平稳自相关过程AR(2)模型实施MMSE调整，不仅可以消除过程自相关性，而且还减少了过程的波动，使过程输出接近目标值。

2.2 仿真验证

为了说明MMSE的调整效应，我们模拟数据进行验证。主要分析验证两个方面：(1）调整消除了过程的自相关；(2）减少了过程波动。

设过程调整输出为et，过程目标值为M，观测样本数为N，则均方误差为

现对 φ1=1.5，φ2=-0.51 的 AR（2）过程进行仿真验证，该过程的一阶自相关函数ρ1=0.99，二阶自相关函数为ρ2=0.99。仿真数据100个，原始数据和调整输出的时间序列图如图2。图2的原始数据虽然未受到特殊原因的影响，由于数据间存在高度正自相关，数据围绕目标值上下徘徊，标准差为σz=10.1，MSE(z)=131.33。对于图2中的调整输出数据检验独立性，其自相关函数如图3所示。从图4中可以看到|ρ^k|，因此，可判断调整后的数据之间相互独立，标准差减少到σe=1，均方误差从131.33减少到MSE(e)=0.95；同样，由于坐标系的纵轴的刻度一样，从图2中也可以看到波动显著的减少。由此验证了调整后的过程更接近目标值，过程得到改进。

3 调整方法

3.1 Grubbs调和规则

现在我们来考虑过程初始设置调整问题。假设过程均值为零，初始设置为X0，由于调整机器设置，过程均值偏离为一个未知常数d，调整后的输出误差为

即：eI=d+X0+εI

这样，为了补偿偏差μI=d+X0，第一次调整量为XI-X0，过程均值水平为

μ2=d+XI

以此类推：μt=d+Xt-I，eI=d+Xt-I+εI

如果已知 μt，理想的调整量为XI-Xt-I=-μt，可以使水平偏离的均方误差达到最小，但是实际中由于μt未知，实际的调整应该基于μt的估计。使用Kalman滤波估计μt，通过估计量使 XI-Xt-I=-μ^t进行调整，则调整规则为

3.2 仿真验证

设过程的初始偏离为d0=5，随机产生100个数据，则过程调整前的输出yt如图4a所示。调整后的偏离为dt，过程调整20次前后的结果如表1所示，调整后的输出et如图4b。图4b中的虚线为5次的Grubbs调整输出序列，实线为20次的Grubbs调整输出序列。

共调整20次，第20次调整后的偏离为0.347，应用这一调整规则的好处是减少了对目标值的偏离。从表1第3列可以得到均方误差和为1.328，而没有调整的第2列的均方误差和为25.13，几乎大了19倍。从表1中还可以得到第5次的调整偏离最小为0.086；如果仅调整5次，则均方误差和为1.237小于调整20次的。

4 结论

MMSE调整效应不仅消除过程数据的自相关，而且还可以减少过程波动。Grubbs调整是调整由系统误差导致过程均值的偏离，过程仍然为统计稳态。这两种调整方法最初是对不同的制造过程问题，由不同理论领域的学者所开发，然而，它们却有其共性，那就是通过对过程进行调整，使输出回归到目标值上。在使用中，如果过程波动直接影响到过程均值，均值的变化表现为时间序列模型可以采用MMSE调整；如果过程波动不直接影响过程均值，而仅仅是系统误差引起，可以采用Grubbs调整。两种方法的调整方式不同，MMSE通过调整输入变量，减少输出对目标值的偏离；而Grubbs调整直接修正过程均值。

表1 Grubbs调整前后的MSE

[1]Cai D.Q.,Xie M.,Goh T.N.SPC in an Automated Manufacturing Environment[J].International Journal of Computer Integrated Manufacturing,2001，14(2).

[2]Gultekin M.,Elsayed E.A.,English J.R.，Hauksdottir A.S.Monitoring Automatically Controlled Processes Using Statistical Control Charts[J].The International Journal of Production Research,2002,（40）.

[3]Box G.E.P.,Kramer T.Statistical Process Monitoring and Feedback Adjustment-A Discussion[J].Technometrics,1992,34(3).

[4]Harris T.J.,Ross W.H.Statistical Process Control Procedure for Correlated Observations[J].Canadian JournalofChemicalEngineering,1991,(69).

[5]Jiang W.,Tsui K.-L.SPC Monitoring of MMSE-and PI-Controlled Processes[J].Journal of Quality Technology,2002,34(4).

[6]E.Del Castillo.A Note on Two Process Adjustment Models[J].Quality and Reliability Engineering International,1998,14(1).

[7]Deming W.E.Out of the Crisis[M].MA:The MIT Press,1982.

[8]MacGregor J.F.A Different View of the Funnel Experiment[J].Journal of Quality Technology,1990,22(4).

[9]Hoerl R.W.,Palm A.C.Integrating SPC and APC[J].Technometrics,1992,34(3).

[10]Keats J.B.,Hubele N.F.Statistical Process Control in Automated Manufacturing[M].New York:Dekker,1989.

[11]Macgregor J.F.Discussion of Statistical Process Monitoring and Feedback Adjustment-Discussion[J].Technometrics,1992,34(3).

[12]MacGregor J.F.On-line Statistical Process Control[J].Chemical Engineering Progress,1998,84(10).