基于误判率的贝叶斯判别法在变形监测点稳定性分析中的应用
陈 超 张献州
(西南交通大学土木工程学院, 四川成都 610031)
在变形监测过程中,监测点的相邻两期坐标之间存在差异,其包含了测量误差和点位稳定性信息[1~2]。为了判断这种差异究竟是测量误差干扰还是点位变动引起的,本文采用基于误判率的贝叶斯判别法对变形监测点的稳定性进行判别。
对于变形监测点的稳定性分析其实是一个分类问题,而且是一个二类分类问题,即稳定类(Ri)和非稳定类(Rj)
式中XΙ、XΠ分别为两期坐标平差值,ΔX为坐标之差。Ri表示两期坐标之差异是由测量误差的干扰引起的,此时点位是稳定的;Rj表示两期坐标之差异虽然存在测量误差的干扰,但主要是由于点位自身的变动引起的,此时点位是非稳定的。
1 贝叶斯判别理论
在分类问题中,往往希望尽量减少分类的错误。从这样的要求出发,利用概率论中的贝叶斯公式,建立基于误判率的目标函数,得到分类规划并对未知点进行判定的方法,称之为贝叶斯判别法[3]。
类别的状态是一个随机变量,而某种状态出现的概率是可以估计的。假设在m维空间中,对两种类别(设类别为R1和R2)进行判定,识别前已知先验概率P(R1)和P(R2),显然有P(R1)+P(R2)=1。则合理的判别规则应为
若P(R1)>P(R2), 则做出属于R1的判断;若P(R1) 显然,如果仅仅按照先验概率判别就会把所有样本点都判别为一类,而根本没有达到把两类样点分开的目的。这是因为先验概率提供的分类信息太少,为此还必须利用对样本进行观测和分析得到的信息,也就是构成样本数据中的m维观测量。在变形监测点的稳定性分析中,我们通常进行的是单点分析,这样就有m=1。则观测样本X在Ri状态下的类条件概率密度就为P(X|Ri),i=1,2。利用贝叶斯公式 (1) 得到的条件概率P(Ri|X)称为状态的后验概率。因此,贝叶斯公式实质是通过观察X把状态的先验概率转化为后验概率。则基于误判率的贝叶斯判别规则为 若P(R1|X)>P(R2|X),则做出属于R1的判断;若P(R1|X) 设变形监测点稳定类和非稳定类的先验概率分别为P(Ri)和P(Rj),则有P(Ri)+P(Rj)=1;两类的类条件概率分别为P(X|Ri)和P(X|Rj)。由于测量误差的存在,两类的条件概率密度的分布在一般情况下总是存在着不同的重叠,在非重叠的区域内,样本可以被正确的区分开;而在重叠的区域内,就不能正确的把样本区分开,从而决定了错误率的大小。如图1,图中Pi(e)和Pj(e)分别为稳定类和非稳定类的错误率,θij为两类条件概率密度分布的交点。 图1 类概率密度分布及错误率示意 由于类概率距离Dij能直接反映类概率密度的分布情况,且又与误判率P(e)密切相关,因此可成为类可分性的一种度量,作为变形监测点的稳定性判别的基准。 设在m维空间里,类概率密度P(X|Ri)的分布服从N(ξi,Σi),P(X|Rj)的分布服从N(ξj,Σj),且根据同精度观测有Σi=Σj=Σ,则有 (2) (2)式中,ξi,ξj,Σ分别为均值矩阵和协方差阵,Dij称为两类之间的马氏距离[5](是类概率距离的一种)。当样本X的各维特征值之间相互独立时,则有 (3) (4) (4)式中ξi,ξj分别为Ri类和Rj类的期望值,σ为两类的方差(两类方差相等)。 由(2)、(3)和(4)式可知,两均值之间的距离越远,且它们的分布越集中(方差越小),则两类的类概率距离(Dij)就越大,反之,Dij越小。由此可知,在两期观测坐标及统计信息确定后,Dij的大小直接反映了两期观测值的可区分度。Dij越大,两类就越容易区分,分类错误率越小;Dij越小,两类越难区分,分类错误率就越大。 当类概率距离确定后,需要考虑该距离是否能区分两期观测值,即评价其优良性,在判别分析中采用误判概率(P(e))来衡量。如果源于Ri(或者Rj)的样品,取值落在Rj(或者Ri)中,那么按照贝叶斯判别规则就会把它误判为Rj(或者Ri)的样品,这种误判的概率为 (5) 由图1可知,分类误判率P(e)为 P(e)=P(Ri)Pi(e)+P(Rj)Pj(e) (6) (6)式中P(Ri)和P(Rj)分别为变形监测点稳定类和非稳定类的先验概率[6~9]。由于变形监测点的稳定性判别属于二类分类问题,且假设两类别出现的概率相等,即P(Ri)=P(Rj)=0.5。同时变形监测点服从方差相同的一维正态分布,即P(X|Ri)服从N(ξi,σ),P(X|Rj)服从N(ξj,σ),因此P(X|Ri)与P(X|Rj)密度分布将关于他们的交点θij(临界值点)对称,即θij为两类空间取值范围Ri与Rj的分界点。即可得 (7) (7)式中Dij为两类之间的马氏距离。则根据(5)式可进一步计算误判率 (8) 由(6)、(7)和(8)可得 (9) 由上式可知,分类误判率P(e)与类概率距离间存在反相关的关系。两类之间的距离越大,误判率越小;距离越小,误判率越大。据此,我们可以通过设置适当的分类误判率,由(9)式反向计算得到合理的判别距离基准,根据基准即可判别变形监测点的稳定性。 (2)计算DⅢ和P(e)。两期观测精度相同,且服从一维正态分布,则由上步算得的σ根据(4)式计算类概率距离DⅢ;并由(9)式计算误判率P(e)。 (3)选择判别基准D0。根据计算所得误判率的大小,综合工程的精度要求,合理的给定一个可接受的误判率P0(e),由(9)式反向计算出判别的基准值D0。 (4)分类判别。根据表1的分类规划进行变形监测点稳定性的判别。 表1 分类规划 设有四点组成的二维(平面)网,按重心基准平差,两期成果列于表2。 表2 平差坐标及其统计信息 传统的做法是采用统计假设检验(t检验),以α=0.05为显著性水平进行t检验,检验结果如表3[10]。 本文采用基于误判率的贝叶斯判别法,根据计算所得的误判率,并为了能与t检验法进行比较,综合考虑,决定选取误判率临界值P0(e)=0.05进行判别。判别结果如表4。 表3 t检验法结果 注:√表示点位发生了显著性位移。下同。 表4 基于误判率的贝叶斯判别结果 (1)本文所述方法对于监测稳定性的判别结果与传统t检验法所得的结果一致,验证了该方法在变形分析中的可行性。 (2)在得出结论的同时还给出了误判率,增强了判别结论的可靠性,与t检验法相比具有一定的优越性。 (3)本文方法可根据具体情况(如计算所得的误判率大小),综合考虑变形监测精度的要求,设置合理的误判率临界值,进而进行分类判别,有效克服了传统t检验法中对于显著性水平α选取的主观性。 [1] 寇新建.变形分析的Bayes估计与检验[J].地壳形变与地震,1994,14(3):21-26 [2] 黄声享,尹晖,蒋 征.变形监测数据处理[M].武汉:武汉大学出版社,2003 [3] 刘耀玲,焦利民.土地评价理论、方法与系统开发[M].北京:科学出版社,2008:132-134 [4] 高惠璇.应用多元统计分析[M].北京:北京大学出版社,2005:176-192 [5] 何 平.数理统计与多元统计[M].成都:西南交通大学出版社,2007:159-163 [6] 王科欣,徐 辉.基于最小错误率与最小风险的贝叶斯分类比较与研究[J].科技信息,2009(23) [7] 王义敏,安锦文.基于最小错误率的SAR图象分割方法研究[J].计算机工程与应用,2006(16):80-82 [8] 包晓敏,汪亚明.基于最小错误率贝叶斯决策的苹果图像分割[J].农业工程学报,2006,22(5):122-124 [9] 沈 虹,汪剑鸣.基于贝叶斯最小错误率的一种新的指纹分割算法[J].微计算机信息,2006,22(1-1):208-210 [10] 陶本藻.自由网平差与变形分析[M].武汉:武汉测绘科技大学出版社,2000:111-114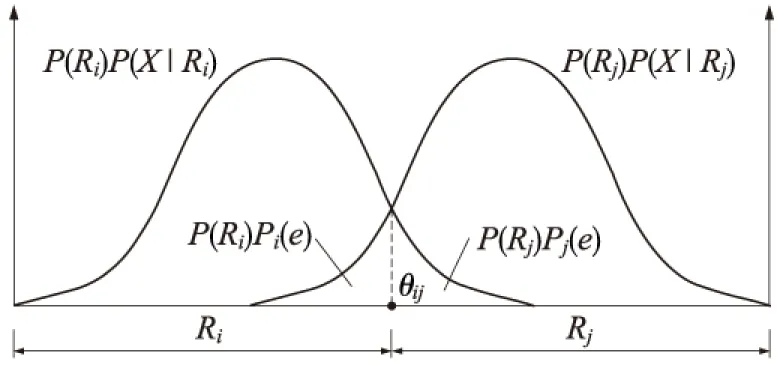
1.1 类概率距离(Dij)
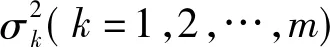
1.2 分类错误率(P(e))
2 分类判别步骤

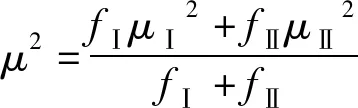

3 应用实例



4 结论

