地下工程测量中联系测量的一种计算方法
裴书琦
(大连九成测绘信息有限公司, 辽宁庄河 116400)
在矿山测量和城市地铁建设等地下隧道工程中,是通过联系测量建立起地面控制点与地下控制点的对应关系,解求出地下导线起算边的坐标方位角和起算点的平面坐标,进而进行地下控制测量、施工测量。在竖井测量中,使用最多的是联系三角形法。通过一井定向建立的是支导线,两井定向建立的是无定向导线[1]。目前的地铁工程中,一般多采用一井定向,贯通距离一般不大于1 km。在作业中,地下导线随隧道的开挖而以支导线的形式向前延伸,受条件的限制,很难组成闭合导线、主付导线进行检查;即使组成了这样的导线,也只是对井下施测精度进行了内符合检验。支导线的最弱点是在导线的终端处,显然,相向对挖的贯通测量在贯通处也将是支导线控制测量的精度最低处。
如何提高贯通测量的控制精度,本文提出了将支导线转化为附合导线的方法。
1 传统的联系三角形法
图1为按传统的联系三角形法进行的一井定向[2],经计算后组成的支导线为:E-D-C-B1-A1-C1-D1-E1。
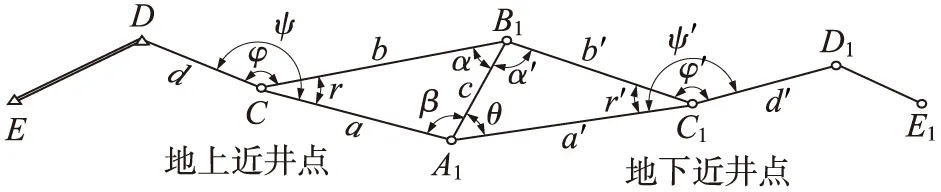
图1 联系三角形法-井定向
联系三角形法要满足一定的图形条件,按文献[3]规定,(以下简称地铁规范),联系三角形的锐角∠r、∠r′宜小于1°,a/c,a′/c宜小于1.5,图形条件要求较高;另外,还要量测a、b、c和a′b′等边长,工作量较大。
在施工标段的工地还没有设置围栏、工棚等设施时,联系测量中能够充分地选择联系三角形的形状,但在工地建成后,无论是进行复测还是检测地下控制导线的精度,都会受到建、构筑物等环境因素的制约,难以选择较理想的联系三角形图形。
2 井下附合导线法
由支导线转化为井下附合导线的思路是:在联系测量后,将支导线的测距边进行方向改化、高程归化和高斯平面的距离改化(一般平差软件均具有这些功能),计算出待定点的坐标,然后选择支导线末端的两个地面高等级控制点,所选的控制点宜位于竖井附近。这里,设想将地面控制点通过垂直投影至井下定向水平(此时变化的只是控制点的高程),我们将投影后的控制点称作虚拟定向点(实际上就是直接使用地面点平面坐标,导线两端的控制点都可增设虚拟定向点)。之后,由相邻支导线点、虚拟定向点的坐标,计算出前后坐标方位角、联系方向角和边长,进而连接形成单一附合导线。
在附合导线的形成中,可将井下两端的待定点直接与定向点相连。计算中采用支导线各待定点的概算坐标为初始值,进行严密平差并评定精度。
图2为井下附合导线的一般形式。

图2 井下附合导线示意
2.1 联系方向角计算
联系方向角是将支导线构建成附合导线的基本概念。联系方向角即水平角,按相邻两已知边的坐标方位角计算,而坐标方位角则通过相邻三个点的坐标(概值)按边长、方位角反算,点的坐标来自于支导线计算。
图2中的∠β1、∠β2、∠β3是联系方向角。设联系方向角为βi,由导线测量可知:
因
αi=αi-1+βi-180° (观测左角)
所以
βi=αi-αi-1+180°
(1)
同理
βi=αi-1-αi+180° (观测右角)
(2)
式中αi为本点至前点的坐标方位角,αi-1为后点至本点的坐标方位角。在图2中β1=αE1-F-αD1-E1+180°。
2.2 井下测量
实际作业中,在投点后,可在投设的两点中选择任意一点设站,以另一点为后视定向,进行支导线测量。如图1中,测站点A1,井下测定的支导线为:B1-A1-C1-D1-E1,连接井上导线。整理后的支导线为:E-D-C-B1-A1-C1-D1-E1。
注意,此时连接井上与井下的B1点处,要涉及到联系方向角∠β3的计算。同样,在点E1、F处,也要按相邻两坐标方位角计算出联系方向角。
另外,若考虑到短边定向的施测精度,可改在C1点设站观测联系三角形中的∠r′及边长a′、b′,由正弦定理解算出∠θ、∠α′后,按∠r′+∠θ+∠α′=180°检核,并将微量闭合差反号平均配赋于∠θ、∠α′,之后,连接地面导线组成支导线计算[2]。
2.3 组成附合导线
附合导线可确定为:E-D-A1-C1-D1-E1,此时的联系方向角为
∠CA1C1=αA1B1-αD1A1+180°+θ
可组成最简附合导线形式:E-D-D1-E1-F-G。
注意:在相向对挖的贯通两侧,控制导线应选择相同的地面控制点组成具有公共定向点的附合导线。
3 算例
以某沿海城市地铁工程中一竖井的联系测量为例,按2.2中的前一种方法测量并组成附合导线计算。依据地铁规范按精密导线施测,采用索佳SET1X型全站仪,标称精度为:测角:±1″,测距:±(1.5+2×10-6D) mm。
施测后的导线全长422.64 m,其中最长边240.152 m,最短边10.767 m,平均边长105.66 m,待定点3个。
概算后的方位角闭合差: +17.51″,导线全长相对闭合差:1/19 776。
经条件平差后的综合精度如下:
最弱点点位中误差为±2.4 mm,最弱相邻点的相对点位中误差1.88 mm,后验单位权中误差为±1.65″。
程序在严密平差后进行了后验方差的假设检验[4],即进行平差模型的正确性检验。采用κ2检验法,检验中的计算统计量κ2=8.21。
取:κ0.9752<κ2<κ0.0252,则κ2∈(0.216,9.348),检验成立,说明平差模型无显著问题。
4 精度分析
按地铁规范对精密导线的技术要求:测角中误差±2.5″,计算后的方位角闭合差应≤±11.18″,导线全长相对闭合差应≤1/35 000,显然上述算例大于此项规定,但地下导线测量受观测条件的制约,不应执行地面精密导线的精度要求。但规范对精密导线以下的技术级别,并没有给出具体规定。
按文献[5],地下导线测量与地面导线测量有如下精度关系
m地下=m地上/0.45
即
m地下=2.2m地上
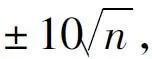
5 结论
本文介绍的技术方法在地下工程的导线测量中具有可行性,特别适用于城市地铁工程测量,并具有以下特点:
(1)可提高贯通测量精度。
(2)可免去陀螺经纬仪(全站仪)作业。
(3)能提高井下施工导线的精度,因施工导线是直接在附合导线形式的基本控制导线下进行的。
(4)对高等级控制点的使用具有灵活性。如当被选用的地面控制点已遭破坏时,只要两点的数学关系(坐标)存在,仍可作为虚拟定向点在附合导线中使用。
(5)对两井定向后所形成的无定向导线(坐标附合导线),可转换为单一附合导线。
(6)当贯通距离较长时,为避免测站过多而导致误差累积传递过大,可舍去若干测点而组成较短的导线,但此时应注意相邻点间精度的均衡性。
(7)对组成的附合导线,因等级较低,也可采用近似平差计算。
(8)该方法对地面控制点稀少地区及较低等级的导线测量,具有一定的参考意义。
6 结束语
本文方法是使用高斯平面坐标反算出水平角和边长,而不是严格意义下的外业直接观测值。另外,在附合导线中若存在地面与地下两种观测值,应视为不等精度观测,这样,在严密平差程序中,对函数关系式、条件(或误差式)方程式的列立及边角权等,应作出相应的设定。可采用附有参数的条件平差的函数模型。
应该说明的是:测量平差是采用实际观测值,本文所提出的方法显然与经典平差理论相悖离。
基于如上考虑,在测量平差理论中可增加约定观测值这一概念,即将观测值分为如下两类。
(1)直接观测值
其观测数据是直接测量采集的结果,或是将测量后的数据经某种变换计算的结果[4]。
(2)约定观测值
凡不是直接观测而是通过某种计算能唯一确定出函数关系的观测量称之为约定观测值。例如:通过导线中待定点的坐标(概值)与已知高等级点坐标反算出的水平角、边长;联系三角形中的α、β(见图1)。约定观测值是一种统计量,属于数理统计中的子样范围,并可以参加严密平差计算解求出未知量的最佳估值。
[1] 朱洪侠.矿山测量[M].重庆:重庆大学出版社,2010
[2] 郑之华.地下工程测量[M].北京:煤炭工业出版社,2007
[3] GB 50308—2008 城市轨道交通工程测量规范[S]
[4] 王穗辉.误差理论与测量平差[M].上海:同济大学出版社,2010
[5] 张正禄,等.工程测量学[M].武汉:武汉大学出版社,2005
[6] GB 50026—2007 工程测量规范[S]

